Complete Solutions to All Questions of chapter FLUID MECHANICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | FLUID MECHANICS |
| HC VERMA | All Questions |
| Number Of Questions | 90 |
| Academic Year | 2023-24 |
Water is filled in a flask up to a height of 20 cm. The bottom of the flask is circular with radius 10 cm. If the atmospheric pressure is `1.01xx10^5` Pa, find the force exerted by the water on the bottom. Take `g=10 ms^-2` and density of water =1000 kgm^-3.
View SolutionA 700 g solid cube having an edge of length 10 cm floats in water. How much volume of the cube is outside the water? Density of water `=1000 kgm^-3`
View SolutionFigure shows a liquid being pushed out of a tube by pressing a piston. The area of cross section of the piston is 1.0 cm^2 and that of the tube at the outlet is `20 mm^2`. If the piston is pushed at a speed of `2cms^-1`. What is the speed of the outgoing liquid?

View SolutionFigure shows a liquid of densith `1200kgm^-3` flowing steadily in a tube of varying cross section. The cross section at a point A is `1.0cm^2` and that at B is `20mm^2`, the points A and B are in the same horizontal plane.The speed of the liquid at A is 10 `cms^-1`. Calculate the difference in pressure at A and B.

View SolutionA water tank is constructed on the top of a building. With what speed will the water come out of a tap 6.0 m below the water level in the tank? Assume steady flow and that the pressure above the water level is equal to the atmospheric pressure
View SolutionA beaker of circular cross-section of radius 4 cm is filled with mercury up to a height of 10 cm. Find the force exerted by the mercury on the bottom of the beaker. The atmospheric pressure `=10^5Nm^-2`. Density of mercury `=13600 kgm^-3. Take g10ms^-2`
View SolutionThe density of asir ner earth's surface is `1.3kgm^-3` and the atmospheric pressure is `1.0xx10^5Nm^-2`. If the atmosphere had uniform density, same as that observed at the surface of the earth what would be the height of the atmosphere to exert the same pressure?
View SolutionThe liquids shown in figure in the two arms are mercury (specific gravity =13.6) and water. If the difference of heights of the mercury columns is 2 cm, find the height of the water column.
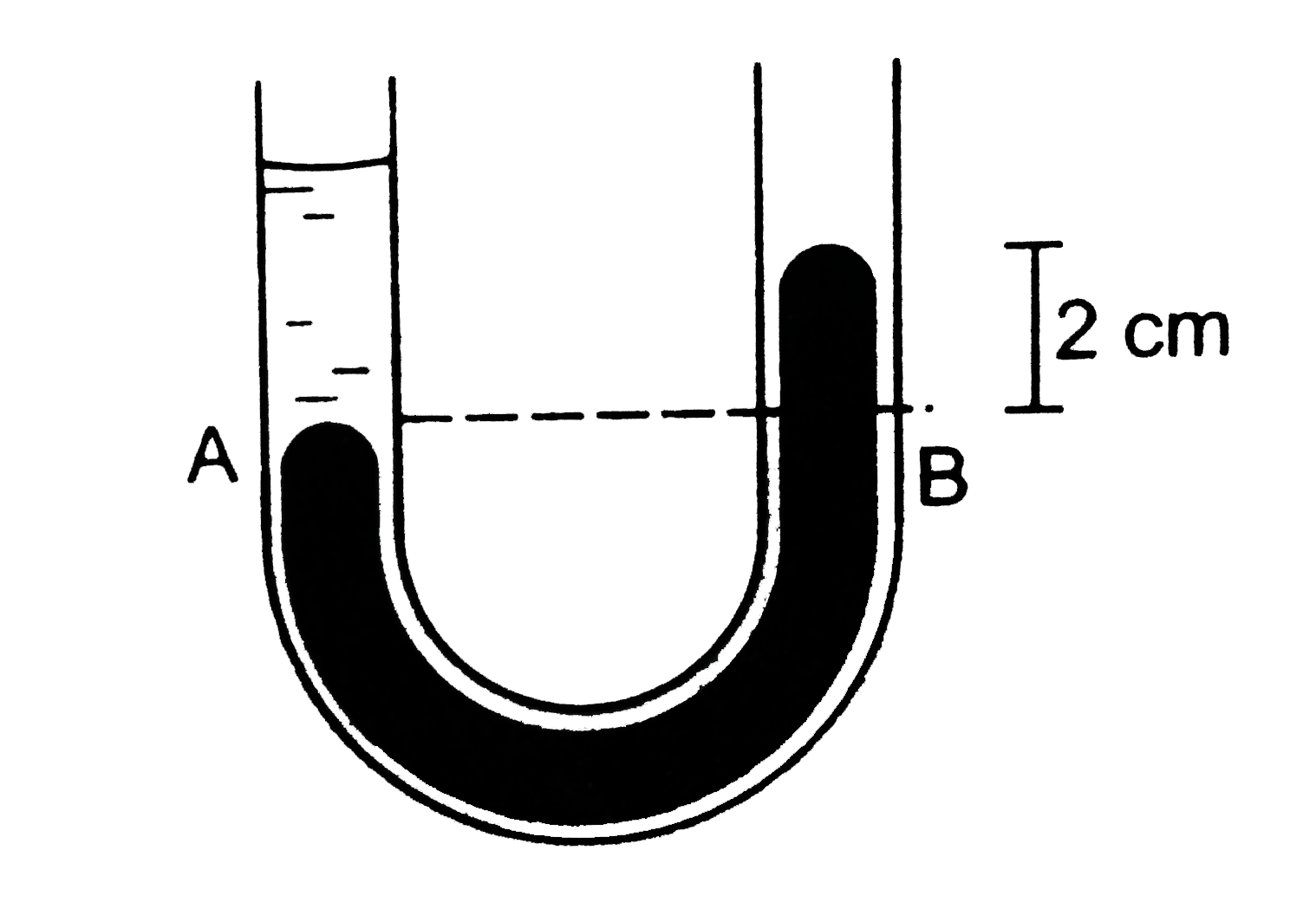 ,
,
View SolutionA cylidrical vesel containing a liquid is closed by a smooth piston of mass m as shown in the figure. The area of cross section of the piston is A. If the atmospheric pressure is `P_0`, find the pressure of the liquid just below the piston.
 ,
,
View SolutionThe area of cross section of the two arms of a hydraulilc press are 1 cm^2 and 10 cm^2 respectively figure. A force of 5N is applied on the water in the thinner arm. What force should be applied on the water in the thicker arm so that the water may remain in equilibrium?
 ,
,
View SolutionA copper piece of mass 10 g is suspended by a vertical spring. The spring elongates 1 cm over its natural length to keep the piece in equilibrium. A beaker containing water is now placed below the piece so as to immerse the piece completely in water. Find the elongation of the spring. Density of copper =9000 kgm^-3. `Take g=10ms^-2`
View SolutionA cubical block of wood of edge 3 cm floats in water. The lower surface of the cube just touches the free end of a vertical spring fixed at the bottom of the pot. Find the maximum weight that can be put on the block without wetting it. Density of wood =`800 kgm^-3` and spring constant of the spring `=50Nm^-1 Take g=10ms^-2`.
 ,
,
View SolutionThe wooden plank of length 1 m and uniform cross section is hinged at one end to the bottom of a tank as shown in figure. The tank is filled with water up to a height of 0.5 m. The specific gravity of the plank is 0.5. Find the angle `theta` that the plank makes with the vertical in the equilibrium position. (Exclude the case `theta=0`)
 ,
,
View SolutionA cylindrical block of wood of mass M is floating n water with its axis vertica. It is depressed a little and then released. Show that the motion of the block is simple harmonic and find its frequency.
View SolutionWater flows in a horizontal tube as shown in figure. The pressure of water changes by 600 N m^-2 between A and B where the areas of cross section are `30cm^2 and 15cm^2 respectively. Find the rate of flow of water through the tube.
 ,
,
View SolutionA area of cross section of a large tank is `0.5m^2`. It has an opening near the bottom having area of cross section `1cm^2`. A load of 20 kg is applied on the water at the top. Find the velocity of the water coming out of the opening at the time when the height of water level is 50 cm above the bottom. Take `g=10ms^-2`
View SolutionIs it always true that the molecules of a dense liquid are heavier than the molecules of a lighter liquid?
View SolutionIf someone presses a pointed needle against your skin, your are hurt. But if someone presses as rod against your skin with the same force you easily tolerate. Explain
View SolutionIn the derivation of `P_1-P_2=rhogz` it was asumed that the liquid is incompressible. Why will this equation not be stictly valid for a compressible liquid?
View SolutionSuppose the density of air at Madras is `rho_0 and `atmosphere pressure is `P_0. If we go up the density and the pressure both decreae. Suppose we wish to calculate the pressure at a height 10 km above Madras. Ilf we use the equation `P_0-P=rho_0gz` will we get a pressure more than the actual or less than the actual? Neglect the variation in g. Does your answr change if you also consider the variation in g?
View SolutionThe free surface of a liquid resting in an inertial frame is horizontal. Does the normal to the free surface pass through the centre of the earth? Think separately if the liquid is a. at te equaltor b. at a pole c. somewhere else.
View SolutionA barometer tube reads 76 cm of mercury. If the tube is gradually inclined keeping the open end immersed in the mercury reservoir, will the length of mercury column be 76 cm, more than 76 cm or less than 76 cm?
View SolutionA one meter long glas tube is open at both ends. One end of the tube is dipped into a mercury cup, the tube is kept vertical and the air is pumped out of the tube by connecting the upper end ot a suction pump. Can mercury be puled up into the pump by this process?
View SolutionA satellite revolves round the earth. Air pressure inside the satellite is maintained at 76 cm of mercury. What will be the height of mercury column in a barometer tube 1m long placed inn the satellite?
View SolutionConsider the barometer shown in figure. If a small hole is made at a point P in the barometer tube, will the mercury come out from this hole?

View SolutionIs Archimedes principle valid in an elevator accelerting up? In a car accelerating on a level road?
View SolutionWhy is it easier to swim in sea water than in fresh water?
View SolutionA glass of water has an ice cube floating in water. The water level just touches the rim of the glass. Will the water overflow when the ice melts?
View SolutionA ferry boat loaded with rocks has to pass under a bridge. The maximum height of the rock is slightly more than the height of the rocks is slightly more than the height of the bridge so tht the boat just fails to pass under the bridge. Should some of the rocks be removed or some more rocks be added?
View SolutionWater is slowly coming out from a vertical pipe. As the water descends after coming out its area of cross section reduces. Explain this on the basis of the equation of continuity.
View SolutionWhile watering a distant plant, a gardener partially closes the exit hole of the pipe by putting his finger on it. Explain why this results in the water stream going to a larger distance.
View SolutionA Gipsy car has a canvas top. When the car runs at high speed, the top bulges out. Explain.
View SolutionA liquid can easily change its shape but a solid can not because
View SolutionConsider the equations
`P=Lim_(/_\srarr0)F/(/_\S) and P_1-P_2=rhogz`
In an elevator acceleratin upward
View SolutionThe three vessels shown in figure have same base area. Equal volumes of a liquid are poured in three vessels. The force on the base will be
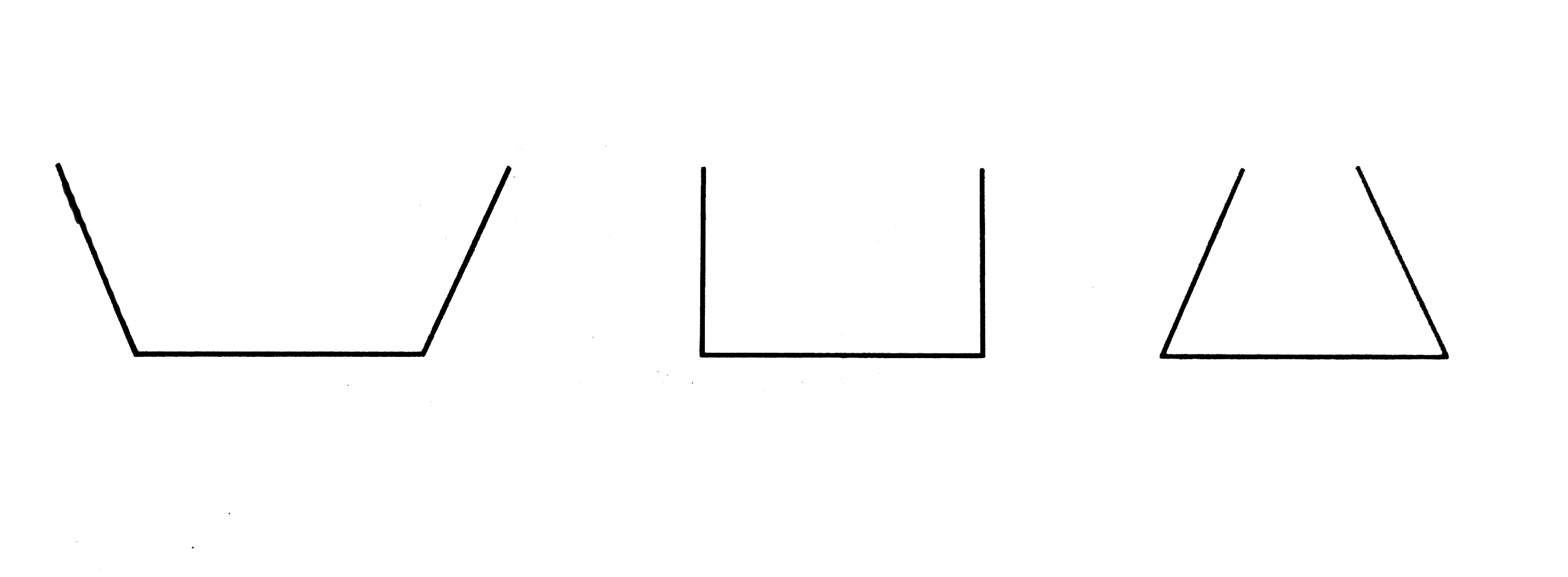
View SolutionEqual mass of three liquids are kept in three identical cylindrical vessels A, B and C. the densities are `rho_A, rho_B, rho_C with rho_Altrho_Bltrho_C`. The force on the base will be
View SolutionFigure shows a siphon. The liquid shown in water. The pressure difference `P_B-P_A` between the points A and B is

View SolutionA beaker containing a liquid is kept inside a big closed jar. If the air inside the jar is continuously pumped out, the pressure in the liquid near the bottom of the liquid will
View SolutionThe pressure in a liquid at two points in the same horizontal plane are equal. Consider an elevator accelerating upward and a car accelerating on a horizontal road. The above statement is correct in
View SolutionSuppose the pressure at the surface of mercury in as barometer tube is `P_1` and the pressure at the surface of mercury in the cup is `P_2`.
View SolutionA barometer kept in an elevator reads 76 cm when it is at rest. If the elevator goes up with increasing speed, the reading will be
View SolutionA barometer kept in an elevator accelerating upward reads 76 cm. The air pressure in the elevator is
View SolutionTo construct a barometer, a tube of length 1m is filled completely with mercury and is inverted in a mercury cup. The barometer reading on a particular day is 76 cm. Suppose a 1m tube is filled with mercury up to 76 cm and then closed by a cork. It is inverted in a mercury cup and the cork is removed. It is inverted in a mercury column in the tube over the surface in the cup will be
View SolutionA block of wood is floating in water in a closed vessel as shown in the figure. The vessel is connected to an air pump. When more air is pushed into the vessel, the block of wood floats with (neglect compressibility of water)

View SolutionA meta cube is plced in an empty vessel. When water is filed in the vessel so that the cubeis completely immersed in the water, the fore on the bottom of the vessel in contact with the cube
View SolutionA wooden object floats in water kept in as beaker. The object is near a side of the beaker figure. Let `P_1,P_2,P_3` be the pressure at the three points A,B and C of the bottom as shown in the figure.

View SolutionA closed cubical box is completely filled with water and is accelerated horizontally towards right with an acceleration a. The resultant normal force by the water on the top of the box.
View SolutionConsider the situations of the previous proble. Let the water push the left wass by a force `F_1` and the right wall byi as force `F_2`.
View SolutionWater enters through end A with speed `v_(1)` and leaves through end B with speed `v_(2)` of a cylindrical tube AB. The tube is always completely fielled with water . Im case I, the tube is horizontal and in case II, it is vertical with end A upwards and in case III, it is vertical with end B upwards. We have `v_(1)=v_(2)` for
View SolutionBernoulli's theorem is based on conservation of
View SolutionWater is flowing through a long horizontal tube. Let `P_A and P_B` be the pressures at two points A and B of the tube
View SolutionWater and mercury are filled in two cylindrical vessels up to same height. Both vessels have a hole in the wall near the bottom. The velocity of water and mercury coming out of the holes are `v_1 and v_2` respectively. Then
View SolutionA large cylindrical tank has a hole of area `A` at its bottom and water is poured into the tank through a tube of cross-sectional area `A` ejecting water at the speed `v`. Which of the following is true?
View SolutionA solid floats in a liquid in a partially dipped position.
View SolutionAn empty balloon weighs `W_(1)`. If air equal in weight to `W` is pumped into the balloon, the weight of the balloon becomes `W_(2)`. Suppose that the density of air inside and outside the balloon is the same. Then
View SolutionA solid is completely immersed in a liquid. The force exerted by the liquid on the solid will
View SolutionA closed vessel is half filled with water. There is a hole near the top of vessel and air is pumped out from this hole.
View SolutionIN a streamine flow
View SolutionWater floows through two identical tubes A and B. A volume `V_0` of water passes through the tube A and `2V_0` through B in a given time. Which of the following may be correct?
View SolutionWater is flowing through a long horizontal tube. Let `P_A and P_B` be the pressures at two points A and B of the tube
View SolutionThere is a small hole near the botton of an open tank filled with liquid. The speed of the water ejected does not depend on
View SolutionThe surface of water in a water tank on the top of a house is 4 m above the tap level. Find the pressure of water at the tap, when the tap is closed. Is it necessary to specify that the tap is closed? Take `g=10ms^-2`
View SolutionThe heights of mercury surfaces in the two arms of the manometer shown in figure are 2 cm and 8cm. Atmospheric pressure `=1.01xx10^5Nm^-2` . Find (a). the pressure of the gas in the cylinder and (b). the pressure of mercury at the bottom of the U tube.

View SolutionThe area of cross section of the wider tube shown in figure is `900 cm^2`. If the boy standing on the piston weights 45 kg, find the difference in the levels of water in the two tubes.

View SolutionA glass full of water has a bottom of area `20 cm^(2)`, top of area `20 cm`, height `20 cm` and volume half a litre.
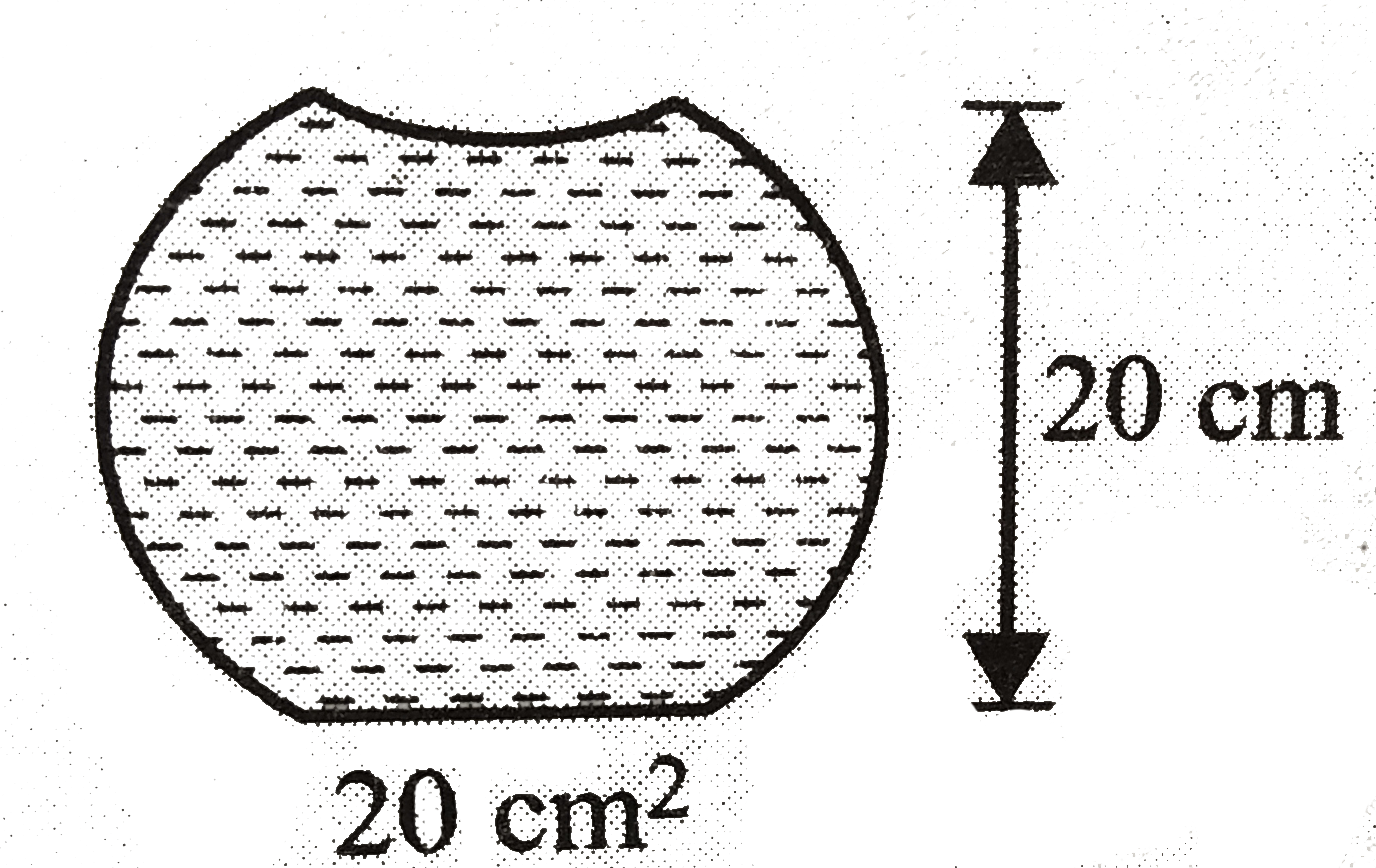
a. Find the force exerted by the water on the bottom.
b. Considering the equilibrium of the `v`, after. find the resultant force exerted by the side, of the glass on the water. Atmospheric pressure `= 1.0 xx 10^(5) N//m^(2)`. Density of water `= 1000 kg//m^(-3)` and `g = 10 m//s^(2)`
View SolutionIf water be used to construct a barometer, what would be the height of water column at a standard atmospheric presure (76cm of mercury)?
View SolutionFind the force exerted by the water on a `2m^2` plane surface of a large stone placed at the bottom of a sea 500 m deep. Does the force depend on the orientation of the surface? Neglect the size of the stone in comparison to the depth of the sea.
View SolutionWater is filled in a rectangular tank of size `3mxx2mxx1m`. a) Find the total force exerted by the water on the bottom surface of the tank. b) Consider a vertical side of area `2mxx1m`. Take a horizontal strip of wide `deltax` metre in this side, situated at a depth of x metre from the surface of water.Find the force by the water on this strip. c) Find the torque of the force calculate in part b) about the bottom edge of this side. d) Find the total force by the water on this side. e) Find the total torque by the water on the side about the bottom edge. neglect the atmospheric pressure and take `=10ms^-2`.
View SolutionAn ornament weighting 36g in air, weighs only 34g in water. Assuming that some copper is mixed with gold to prepare the ornament, find the amount of copper in it. Specific gravity of gold is 19.3 and that of copper is 8.9.
View SolutionA metal piece of mass 160 g lies in equilibrium inside a glass of water as shown in figure. The piece touches the bottom of the glass at a small number of points. If the density of the metal is `8000 kg m^-3`, find the normal fore exerted by the bottom of the glass on the metal piece.

View SolutionA ferry boat has internal volume `1m^3` and weight 50 kg. a. Neglecting the thickness of the wood, find the fraction of the volume of the boat immersed in water. b. If a leak develops in the bottom and water starts coming in, what fraction of the boat's volume will be filled with water before water starts coming in from the sides?
View SolutionA cubical block of ice floating in water has to support a metal piece weighing 0.5 kg. What can be the minimum edge of the block so that it does not sink in water? specific gravity of ice=0.9.
View SolutionA cube of ice floats partly in water and partly in K.oil figure. Find the ratio of the volume of ice immersed in water to that in K.oil. Specific gravity of K.oil is 0.8 and that of ice is 0.9.
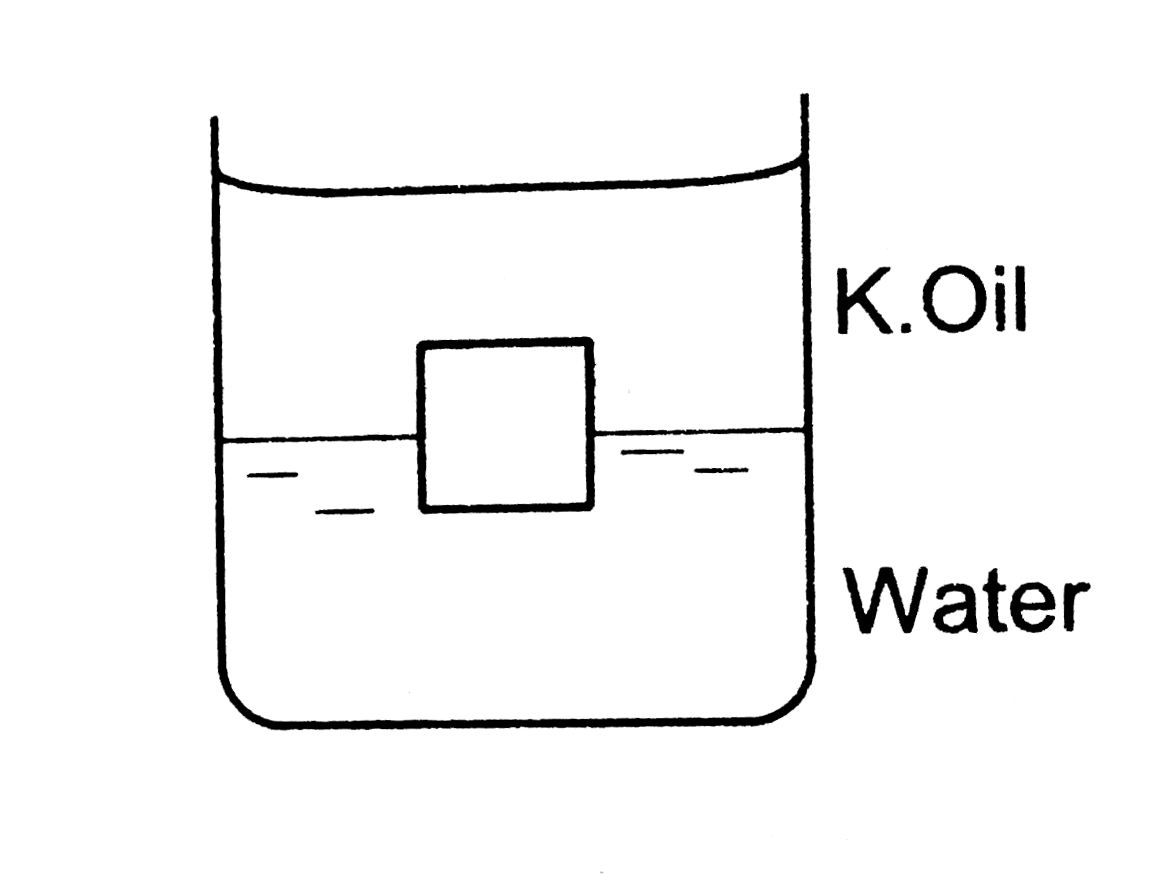
View SolutionA cubical box is to be constructed with iron sheets 1 mm in thickness. What can be the minimum value of the external edge so that the cube does not sink in water? Density of iron `=8000kg m^-3`and density of water `=1000 kgm^-3`.
View SolutionA cubical block of wood weighing 200 g has a lead piece fastened underneath. Find the mass of the lead piece which will just allow the block of float in water. Specific gravity of wood is 0.8 and that of lead is 11.3.
View SolutionA cubical metal block of edge 12 cm floats in mercry with one fifth of the height inside the mercury. Water poured till the surface of the block is just immersed in it. Find the height of the water column to be poured. Specific gravity of mercury =13.6.
View SolutionA hollow spherical body of inner and outer radii 6 cm, and 8 cm respectively floats half submerged in water. Find the density of the material of the sphere.
View SolutionA solid sphere of radius 5 cm floats in water. If a maximum load of 0.1 kg can be put on it without wetting the load, find the specific gravity of the material of the sphere.
View SolutionFind the ratio of the weights, as measured by a spring balance, of a 1 kg block of iron and a 1kg block of wood. Density of iron `=7800 kg m^-3` density of wood `=800 kg m^-3` and density of air `=1.293 kgm^-3`.
View SolutionA cylindrical object of outer diameter 20 cm and mass 2 kg floats in water with its axis vertical. If it is slightly depressed and then released, find the time period of the resulting simple harmonic motion of the object.
View SolutionA cylindrical object of outer diameter 10 cm, height 20 cm and density 8000 `kgm^-3` is supported by a vertical spring and is half dipped in water as shown in figure. a. Find the elongation of the spring in equilibrium condition. b. If the object is slightly depressed and released, find the time period of resulting oscillations of the object. The spring constant `=500 Nm^-1`.

View SolutionA wooden block of mass 0.5 kg and density 800 `kgm^-3` is fastened to the free end of a vertical spring of spring constant 50 `Nm^-1` fixed at the bottom. If the entire system is completely immersed in water, find a. the elongation (or compression) of the spring in equilibrium and b. the time period of vertical oscillations of the block when it is slightly depressed and released.
View SolutionAn ice cube of edge a is placed in an empty cylindrical vessel of radius 2a. Find the edge (in cm) of ice cube when it just leaves the contact with the bottom assuming that ice melts uniformly maintaining its cubical shape. Take a = 12 `pi` cm (Ice is lighter than water)
View SolutionA U-tube containing a liquid is accelerated horizontally with a constant acceleration `a_0`. If the separation between the vertical limbs is l find the difference in the heights of the liquid in the two arms.
View SolutionAt Deoprayag (Garhwal, UP) river Alaknanda mixes with the river Bhagirathi and becomes river Ganga. Suppose Alaknanda has a width of 12 m, Bhagirathi has a width of 8m and Ganga has a width of 16m. Assume that the depth of water is same in the three rivers. Let the average speed of water in Alaknanda be `20 kmh^-1` and in Bhagirathi be `16 kmh^-1`. Find the average speed of water in the river Ganga.
View SolutionWater flows through a horizontal tube of variable cross-section. The area of cross section at A and B are `4 mm^2 and 2mm^2` respectively. If 1 cc of water enters per seconds through. A find a. The speed of water at A, b. the speed of river at B and c. the pressure difference `P_A-P_B`.

View SolutionWater flows through a tube shown in figure. The areas of cross section at A and B are `1cm^2 and 0.5 cm^2` respectively. The height difference between A and B is 5cm. If the speed of water at A is 10 `cms^-1`. Find a. the speed at B and b. the difference in pressures at A and B.

View SolutionWater flows through a horizontal tube as shown in figure. If the difference of heights of water colun in the vertical tubes is 2 cm and the area of cross section at A and B are `4cm^2 and 2cm^2` respectively, find the rate of flow of water across any section.

View SolutionWater flows through the tube shown in figure. The areas of cross section of the wide and the narrow portions of the tube are `5cm^2 and 2cm^2` respectively. The rate of flow of water through the tube is `500 cm^3s^-1` . Find the difference of mercury levels in the U-tube.

View SolutionWater level is maintained ina cylindrical vessel up to a fixed height H. The vessel is kept on a horizontal plane. At what height above the bottom should a hole be made in the vessel so that the water stream coming out of the hole strikes the horizontal plane at the greatest distance from the vessel.

View Solution
All Questions questions and complete solutions for chapter FLUID MECHANICS of HC VERMA PHYSICS (ENGLISH) of Class 11