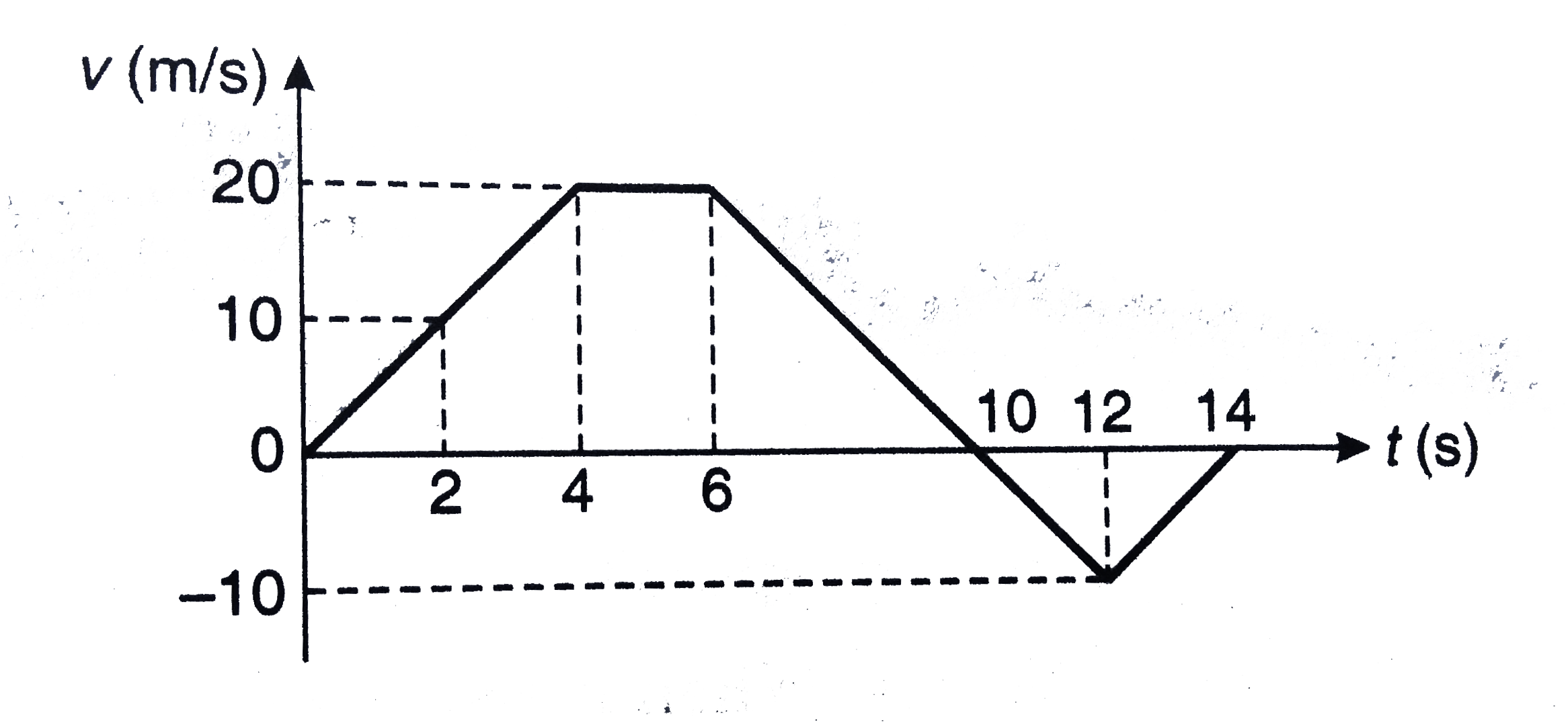Assertion And Reason from DC PANDEY ENGLISH KINEMATICS for Class 11
| Class 11 | PHYSICS |
| Chapter | KINEMATICS |
| DC PANDEY ENGLISH | Assertion And Reason |
| Medium | English |
| Academic Year | 2023-2024 |
Question 2
velocity and acceleration of a particle at some instant are
v=(3ˆi−4ˆj+2ˆk)m/sanda=(2ˆi+ˆj−2ˆk)m/s2
(a) What is the value of dot product of v and a at the given instant?
(b) What is the angle between v and a, acute, obtuse or 90∘?
(c) At the given instant, whether speed of the particle is increasing, decreasing or constant?View SolutionQuestion 11
A particle is moving in a circle of radius 4cm with constant speed of 1cm/s. Find
(a) time period of the particle.
(b) average speed, average velocity and average acceleration in a time interval from t=0 to t=T4. Here, T is the time period of the particle. Give only their magnitudes.View SolutionQuestion 22
A particle starts with an initial velocity 2.5m/s along the posiive x-direction and it accelerates uniformly at the rate 0.50m/s2.
(a) Find the distance travelled by it in the first two seconds
(b) How much time does it take to reach the velocity 7.5m/s ?
(c) How much distance will it cover in reaching the velocity 7.5m/s?View SolutionQuestion 32
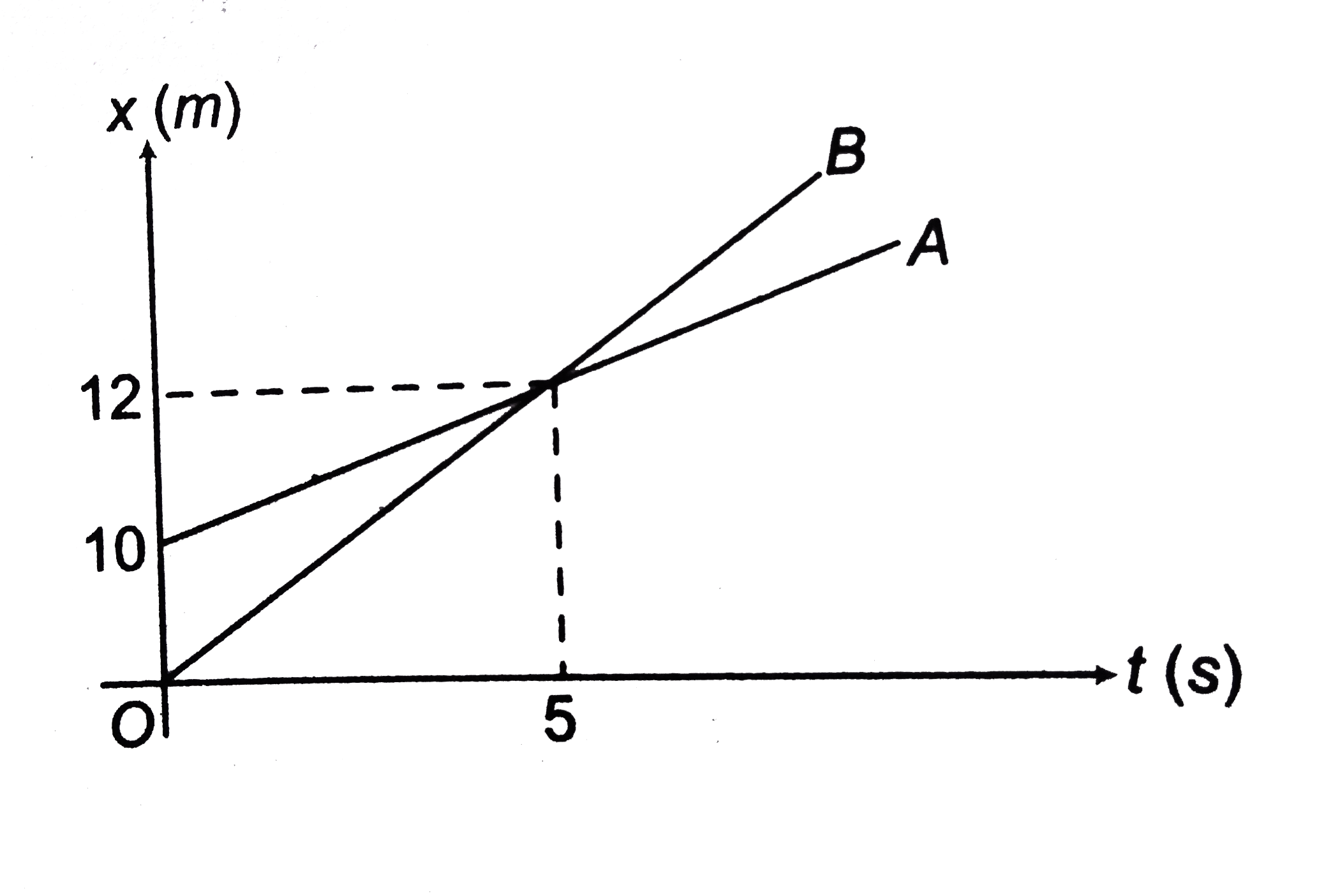
Two particles A and B are moving along x-axis. Their x-coordinate versus time graphs are as shown below
(a) Find the time when the particles start their journey and the x-coordinate at that time.
(b) Find velocities of the two particles.
(c) When and where the particles strike with each other.View SolutionQuestion 39
A river 400m wide is flowing at a rate of 2.0m/s. A boat is sailing at a velocity of 10.0m/s with respect to the water In a direction perpendicular to the river.
(a) Find the time taken by the boat to reach the opposite bank.
(b) How far from the point directly opposite to the starting point does the boat reach the opposite bank?View SolutionQuestion 40
An aeroplane has to go from a point A to another point B, 500km away due 30∘ east of north. Wind is blowing due north at a speed of 20m/s. The air-speed of the plane is 150m/s. (a) Find the direction in which the pilot should head the plane to reach the point B. (b) Find the time taken by the plane to go from A to B.View SolutionQuestion 42
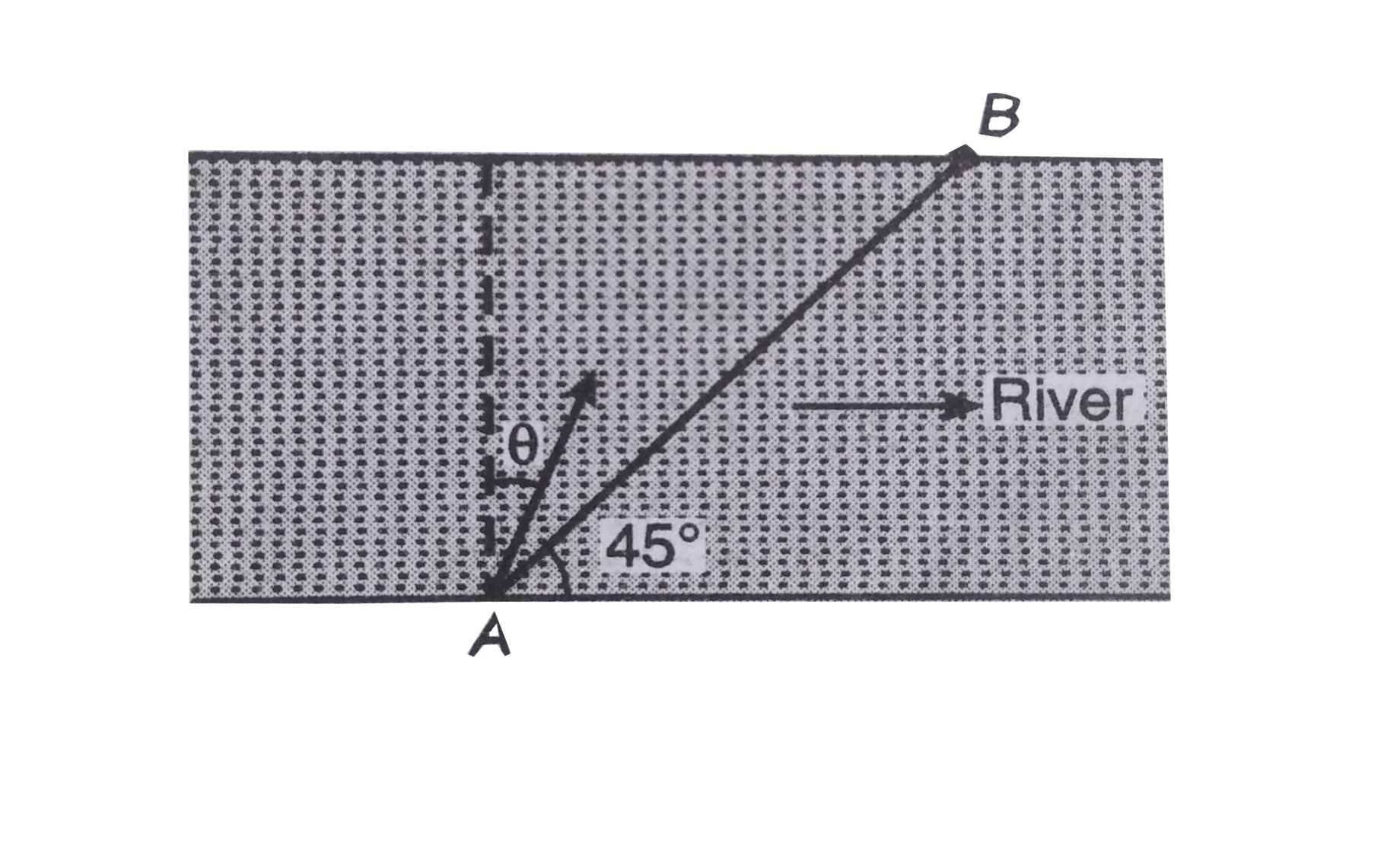
A river is 20m wide. River speed is 3m/s. A boat starts with velocity 2√2m/s at angle 45∘ from the river current (relative to river)
(a) Find the time taken by the boat to reach the opposite bank.
(b) How far from the point directly opposite to the starting point does the boat reach the opposite bank?View SolutionQuestion 54
Assertion : Two bodies of unequal masses m1andm2 are dropped from the same height. If the resistance offered by air to the motion of both bodies is the same, the bodies will reach the earth at the same time.
Reason : For equal air resistance, acceleration of fall of masses m1andm2 will be different.View SolutionQuestion 71
A cart is moving horizontally along a straight line with constant speed 30ms−1. A particle is to be fired vertically upwards from the moving cart in such a way that it returns to the cart at the same point from where it was projected after the cart has moved 80m. At what speed (relative to the cart) must the projectile be fired? (Take g=10ms−2)View SolutionQuestion 75
Two trains are moving with velocities v1=10ms−1andv2=20ms−1 on the same track in opposite directions. After the application of brakes if their retarding rates are a1=2ms−2anda2=1ms−2 respectively, then the minimum distance of separation between the trains to avoid collision isView SolutionQuestion 87
A farmer has to go 500 m due north, 400 m due east and 200 m due south to reach his field. If he takes 20 min to reach the field.
(a) What distance he has to walk to reach the field ?
(b) What is the displacement from his house to the field ?
(c) What is the average speed of farmer during the walk ?
(d) What is the average velocity of farmer during the walk ?View SolutionQuestion 88
A rocket is fired vertically up from the ground with a resultant vertical acceleration of 10m/s2. The fuel is finished in 1 min and it continues to move up. (a) What is the maximum height reached? (b) Afte2r how much time from then will the maximum height be reached?(Take g=10m/s2)View SolutionQuestion 103
A particle is moving in x-y p1ane.At time t=0, particle is at (1m,2m) and has velocity (4ˆi+6ˆj)m/s. At t=4s, particle reaches at (6m,4m) and has velocity (2ˆi+10ˆj)m/s. In the given time interval, find
(a) average velocity,
(b) average acceleration and
(c) from the given data, can you find average speed?View SolutionQuestion 106
A football is kicked vertically upward from the ground and a student gazing out of the window sees it moving upwards past her at 5.00m/s. The window is 15.0m above the ground. Air resistance may be ignored. Take g=10m/s2.
(a) How high does the football go above ground?
(b) How much time does it take to go from the ground to its highest point?View SolutionQuestion 107
A car moving with constant acceleration covered the distance between two points 60.0m apart in 6.00s. Its speed as it passes the second point was 15.0m/s.
(a) What is the speed at the first point?
(b) What is the acceleration?
(c) At what prior distance from the first was the car at rest?View SolutionQuestion 108
A particle moves along the x-direction with constant acceleration. The displacement, measured from a convenient position, is 2 m at time t=0 and is zero when t=10s. If the velocity of the particle is momentary zero when t=6s, determine the acceleration a and the velocity v when t=10s.View SolutionQuestion 109
At time t=0, a particle is at (2m,4m). It starts moving towards positive x-axis with constant acceleration 2m/s2 (initial velocity=0). After 2 s, an additional acceleration of 4m/s2 starts acting on the particle in negative y-direction also. Find after next 2 s.
(a) velocity and
(b) coordinates of particle.View SolutionQuestion 112
A particle moves along a horizontal path, such that its velocity is given by v=(3t2−6t)m/s, where t is the time in seconds. If it is initially located at the origin O, determine the distance travelled by the particle in time interval from t=0 to t=3.5s and the particle's average velocity and average speed during the same time interval.View SolutionQuestion 116
A particle of mass m is released from a certain height h with zero initial velocity. It strikes the ground elastlcally (direction of its velocity is reversed but magnitude remains the same). Plot the graph between its kinetic energy and time till it returns to its initial position.View SolutionQuestion 119
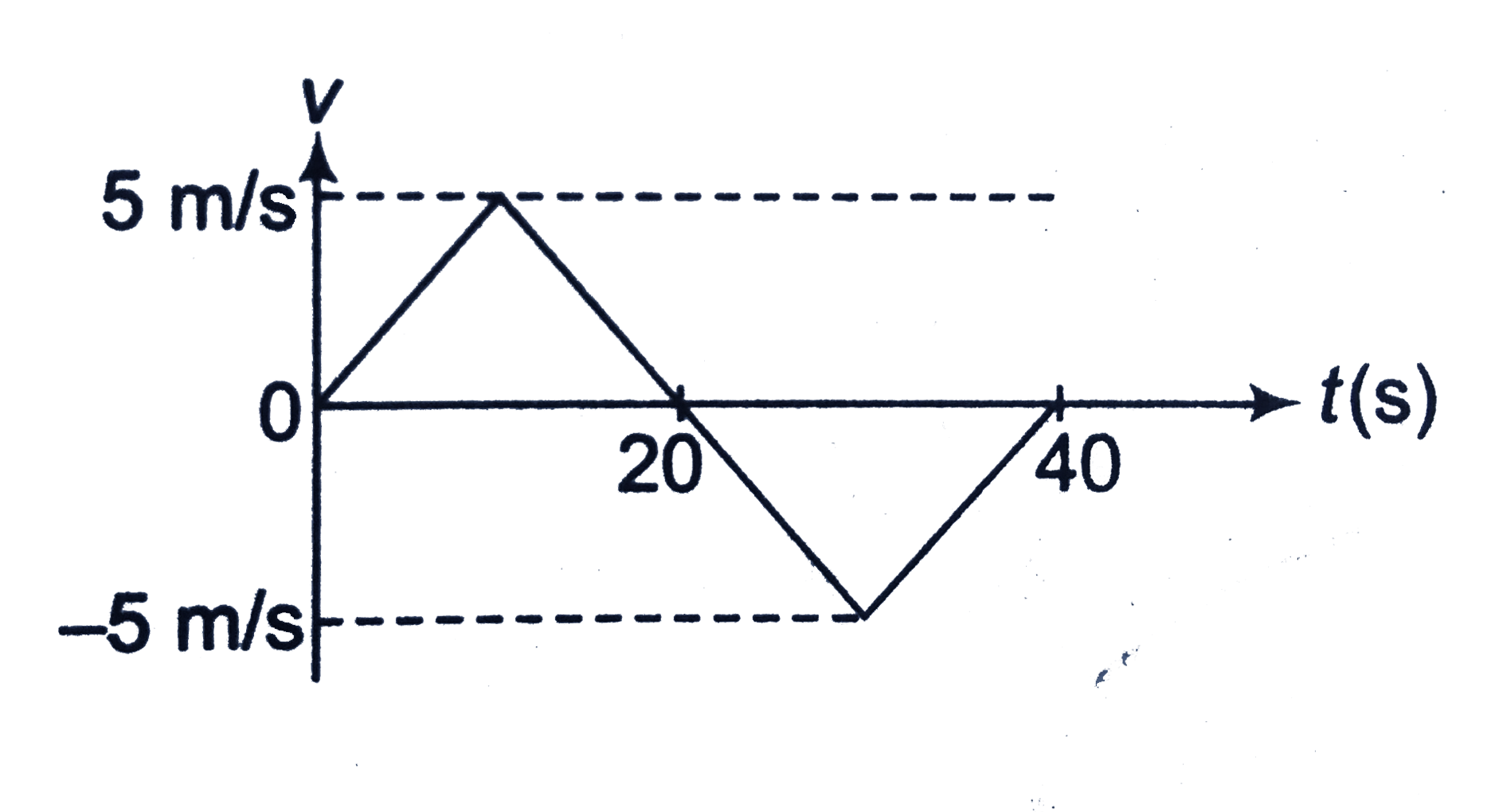
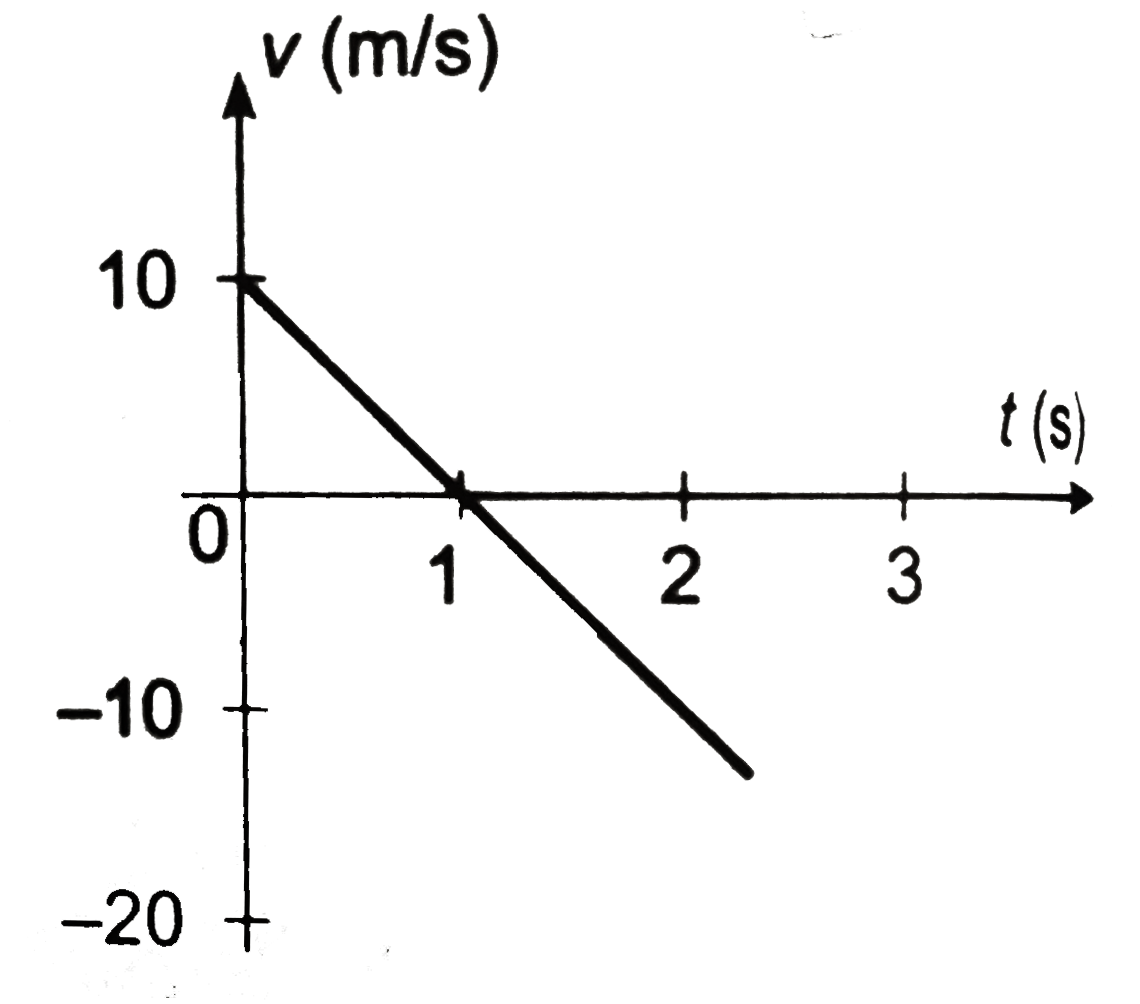
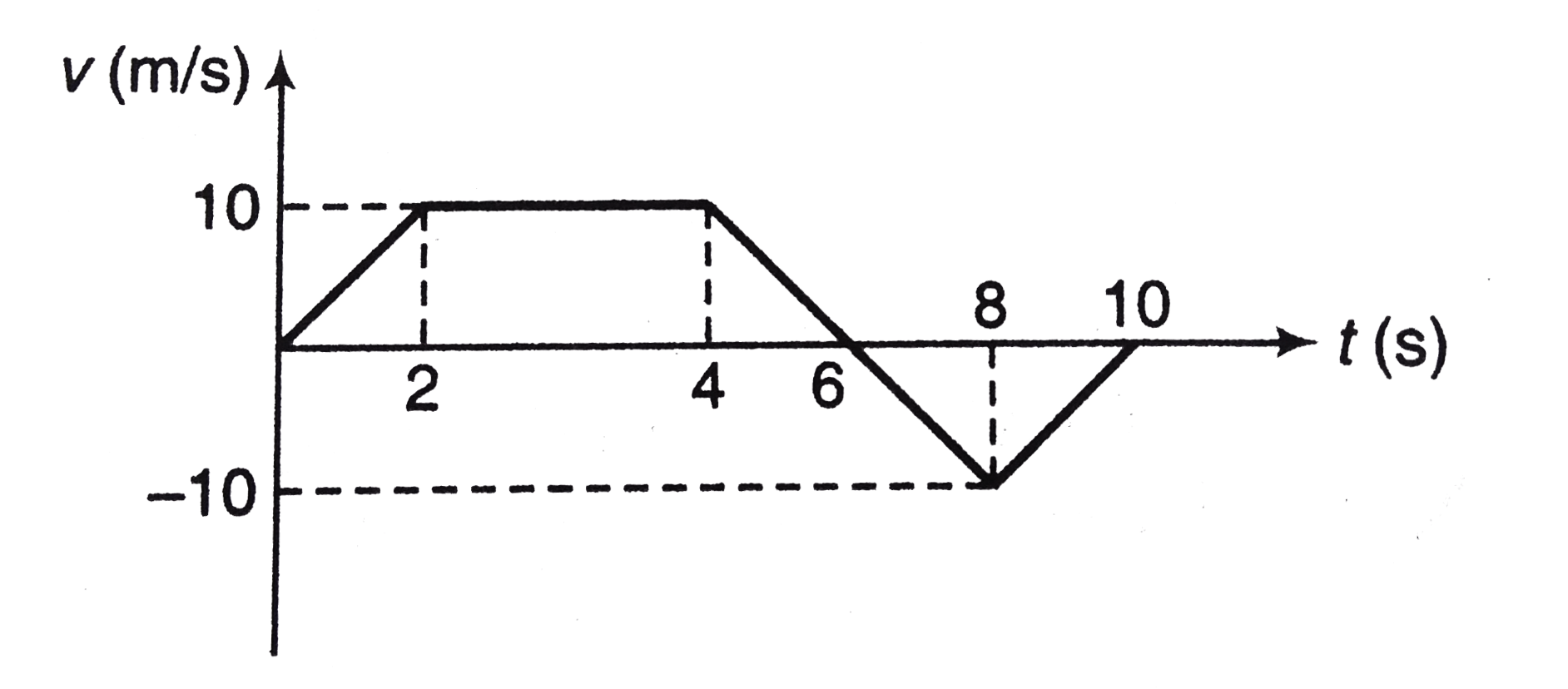
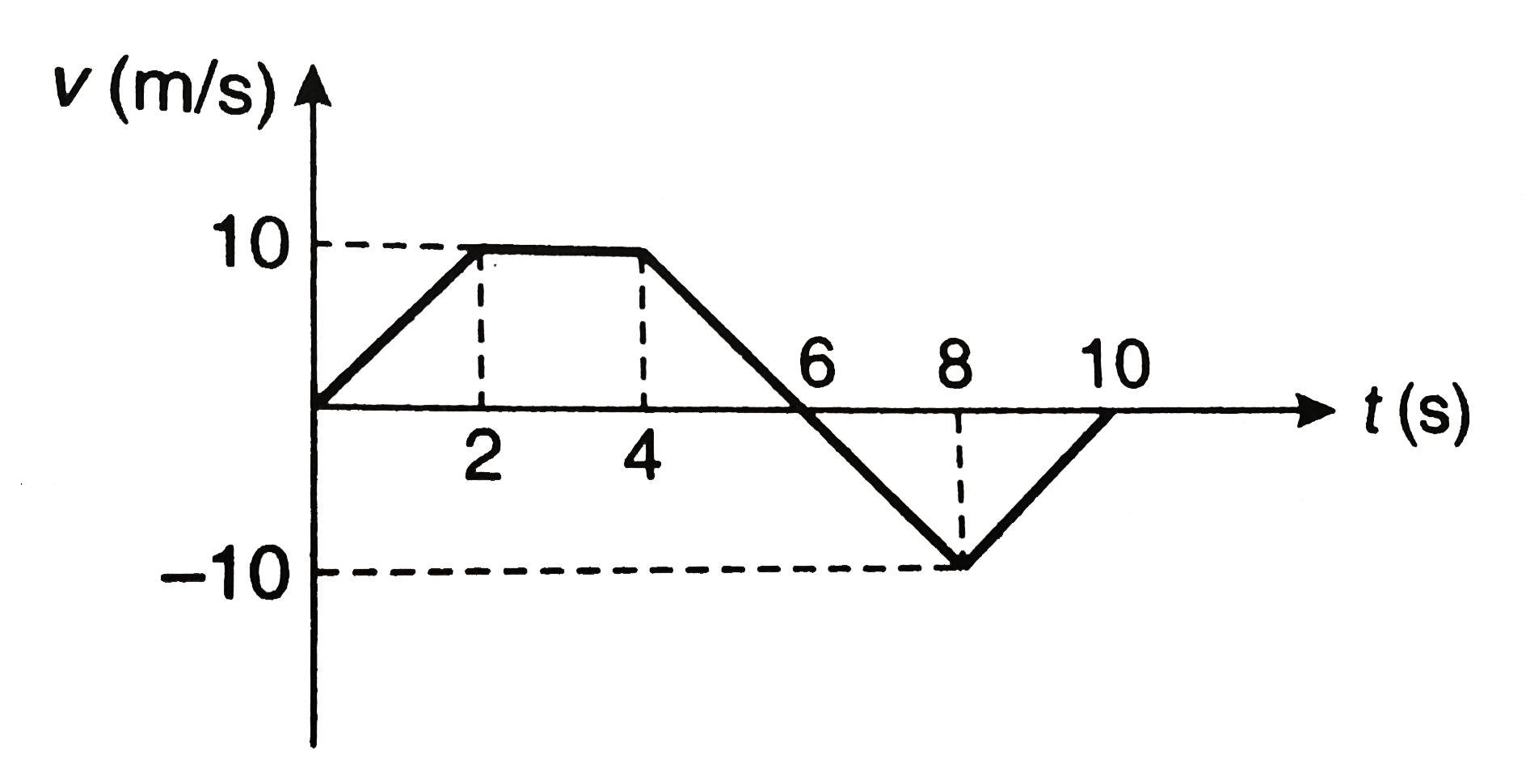
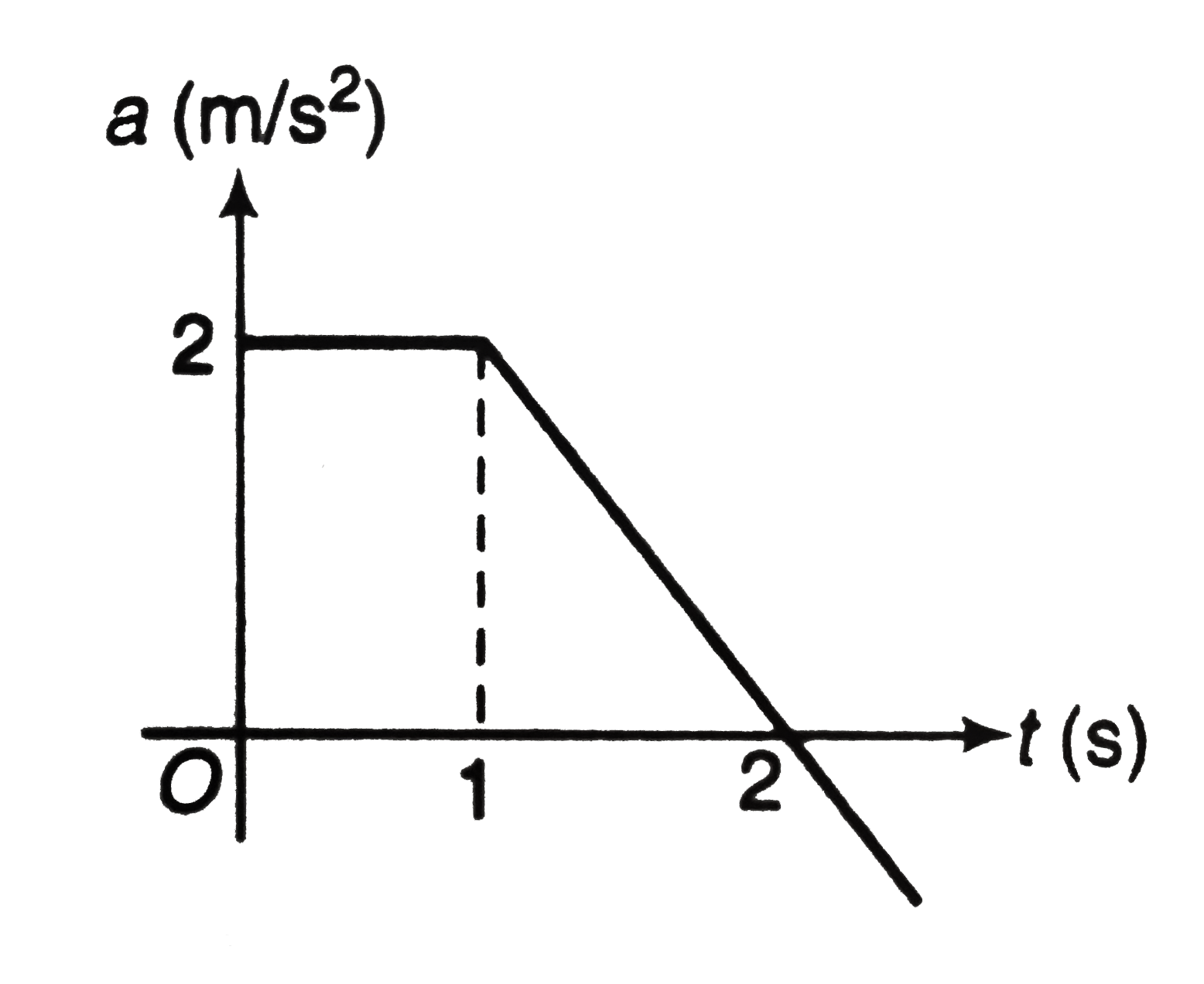
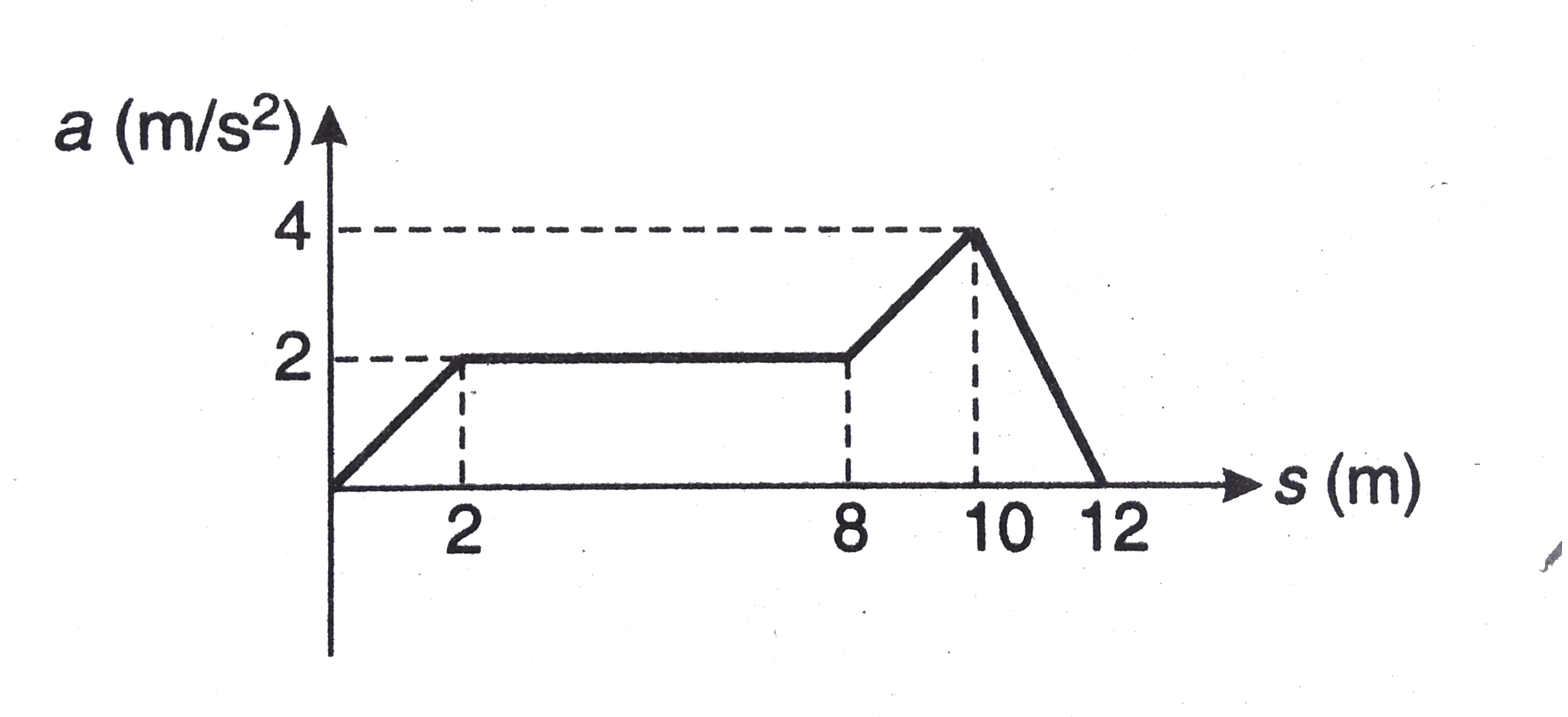
Velocity-time graph of a particle moving in a straight line is shown in figure. At time t=0, displacement of the particle from mean position is 10 m. Find
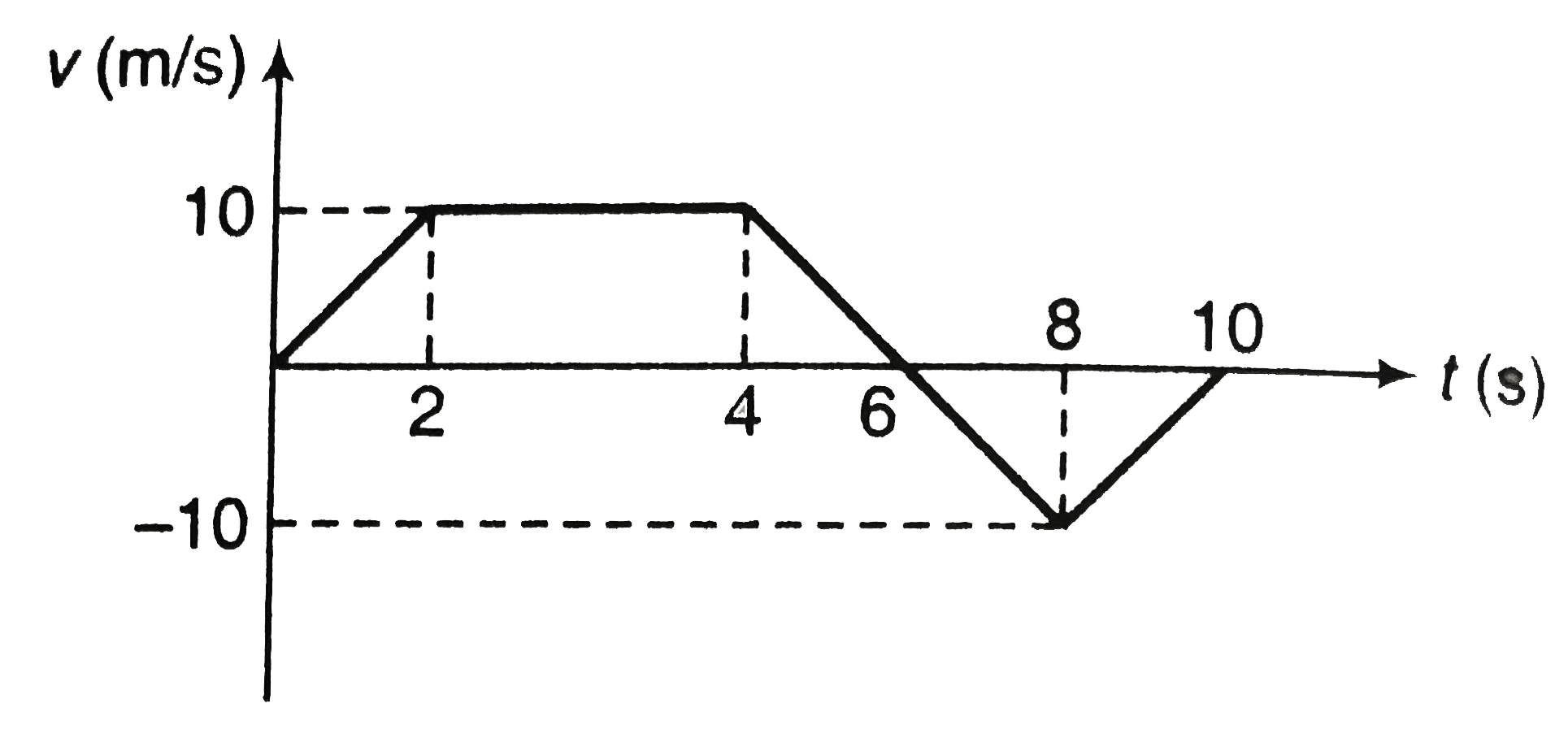
(a) acceleration of particle at t=1s,3sand9s.
(b) position of particle from mean position at t=10s.
(c) write down s-t equation for time interval (i)0≤t≤2s, (ii) 4s≤t≤8sView SolutionQuestion 120
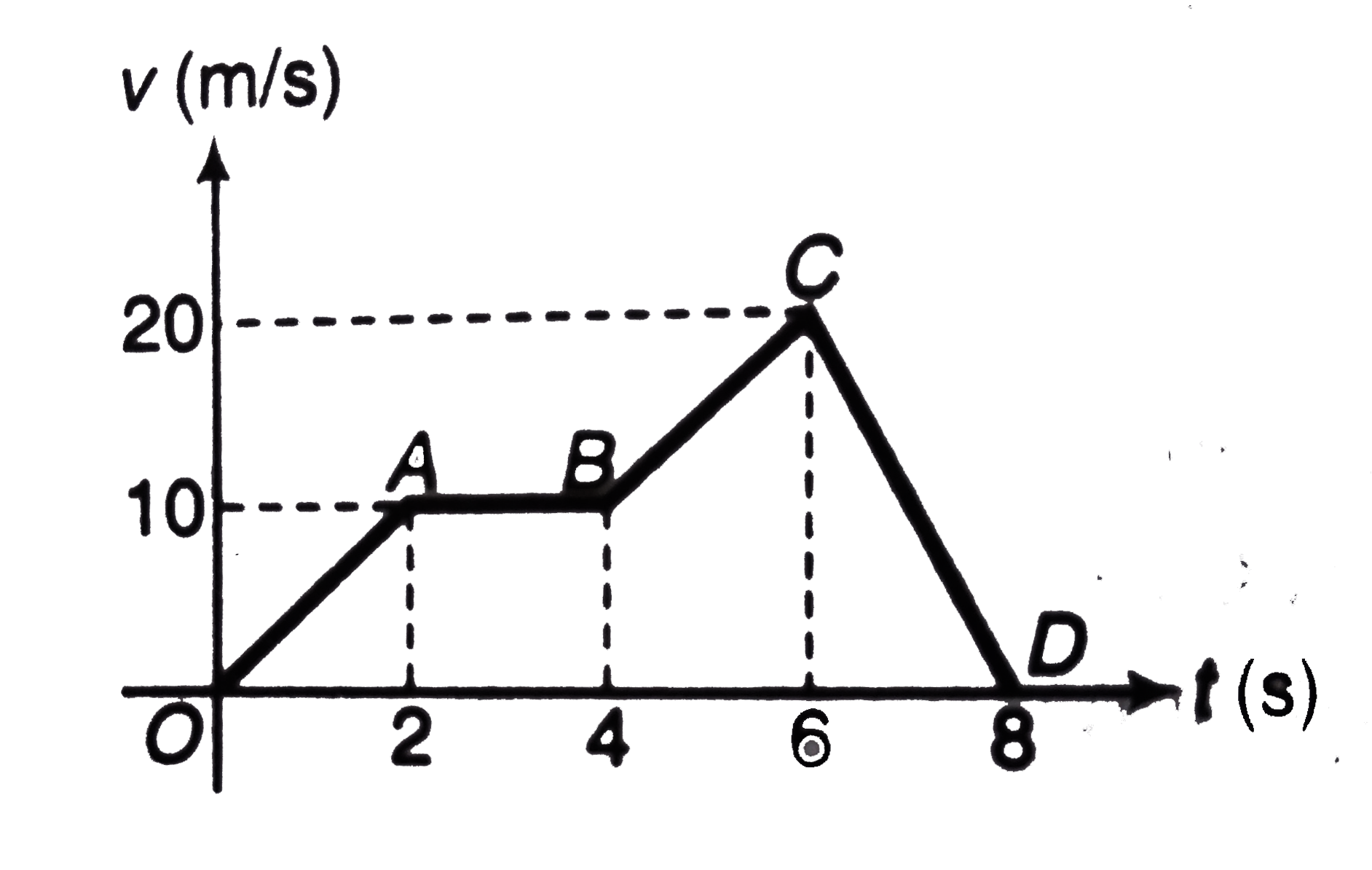
Two particles 1 and 2 are thrown in the directions shown in figure simultaneously with velocities 5m/sand20m/s. Initially, particle 1 is at height 20 m from the ground. Taking upwards as the positive direction, find
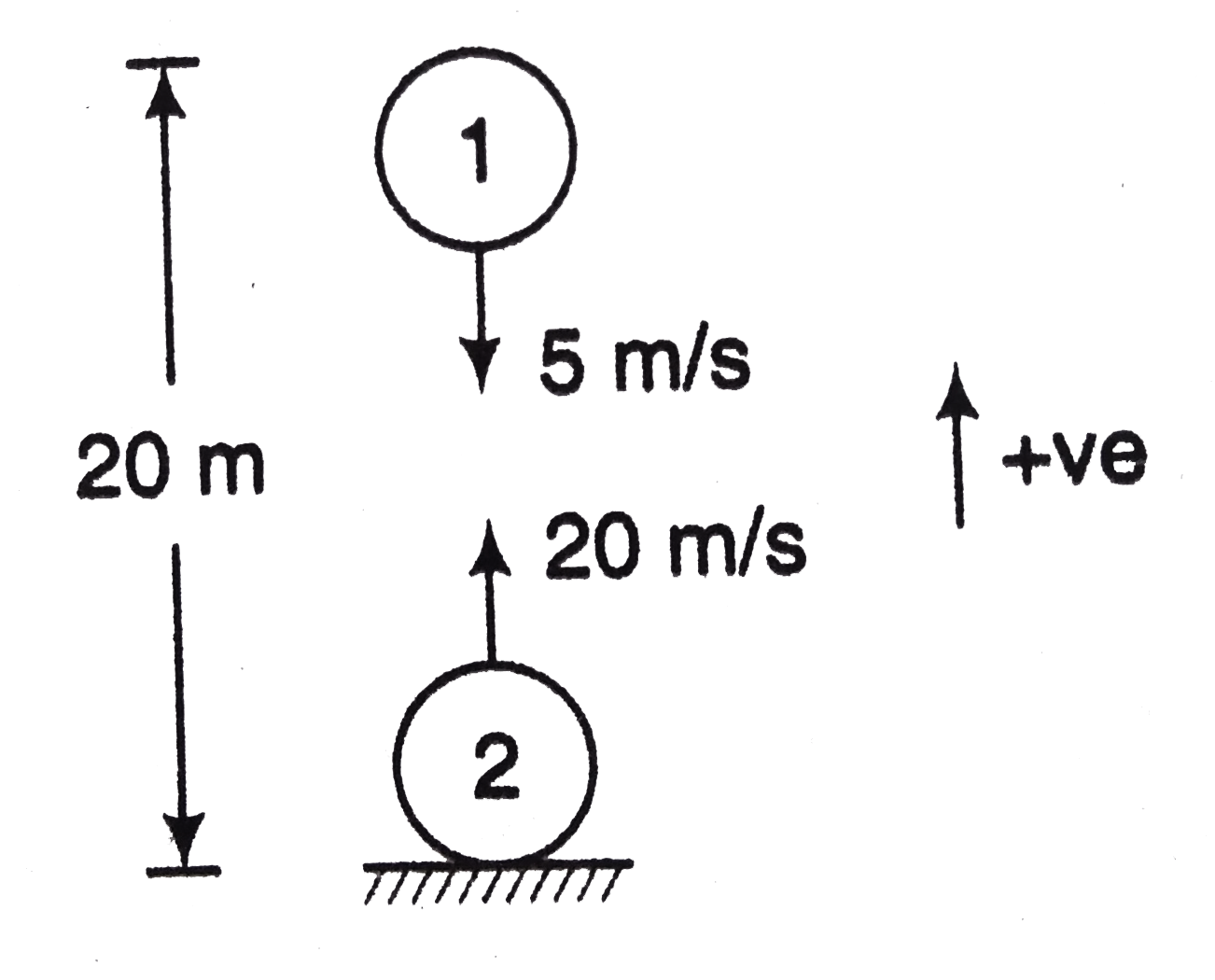
(a) acceleration of 1 with respect to 2
(b) initial velocity of with respect to 1
(c) velocity of 1 with respect to 2 after time t=12s
(d) time when the particles will collide.View SolutionQuestion 121
A ball is thrown vertically upward from the 12 m level with an initial velocity of 18m/s. At the same instant an open platform elevator passes the 5 m level, moving upward with a constant velocity of 2m/s. Determine (g=9.8m/s2 )
(a) when and where the ball will meet the elevator,
(b) the relative velocity of the ball with respect to the elevator when the ball hits the elevator.View SolutionQuestion 122
An automobile and a truck start from rest at the same instant, with the automobile initially at some distance behind the truck. The truck has a constant acceleration of 2.2m/s2 and the automobile has an acceleration of 3.5m/s2. The automobile overtakes the truck when it (truck) has moved 60 m.
(a) How much time does it take the automobile to overtake the truck ?
(b) How far was the automobile behind the truck initially ?
(c) What is the speed of each during overtaking ?View SolutionQuestion 124
An aeroplane has to go from a point P to another point Q, 1000 km away due north. Wind is blowing due east at a speed of 200km/h. The air speed of plane is 500km/h.
(a) Find the direction in which the pilot should head the plane to reach the point Q.
(b) Find the time taken by the plane to go from P to Q.View SolutionQuestion 126
When a man moves down the inclined plane with a constant speed 5ms−1 which makes an angle of 37∘ with the horizontal, he finds that the rain is falling vertically downward. When he moves up the same inclined plane with the same speed, he finds that the rain makes an angle θ=tan−1(78) with the horizontal. The speed of the rain isView SolutionQuestion 129
Velocity of the river with respect to ground is given by v0. Width of the river is d. A swimmer swims (with respect to water) perpendicular to the current with acceleration a=2t (where t is time) starting from rest from the origin O at t=0. The equation of trajectory of the path followed by the swimmer is
View SolutionQuestion 131
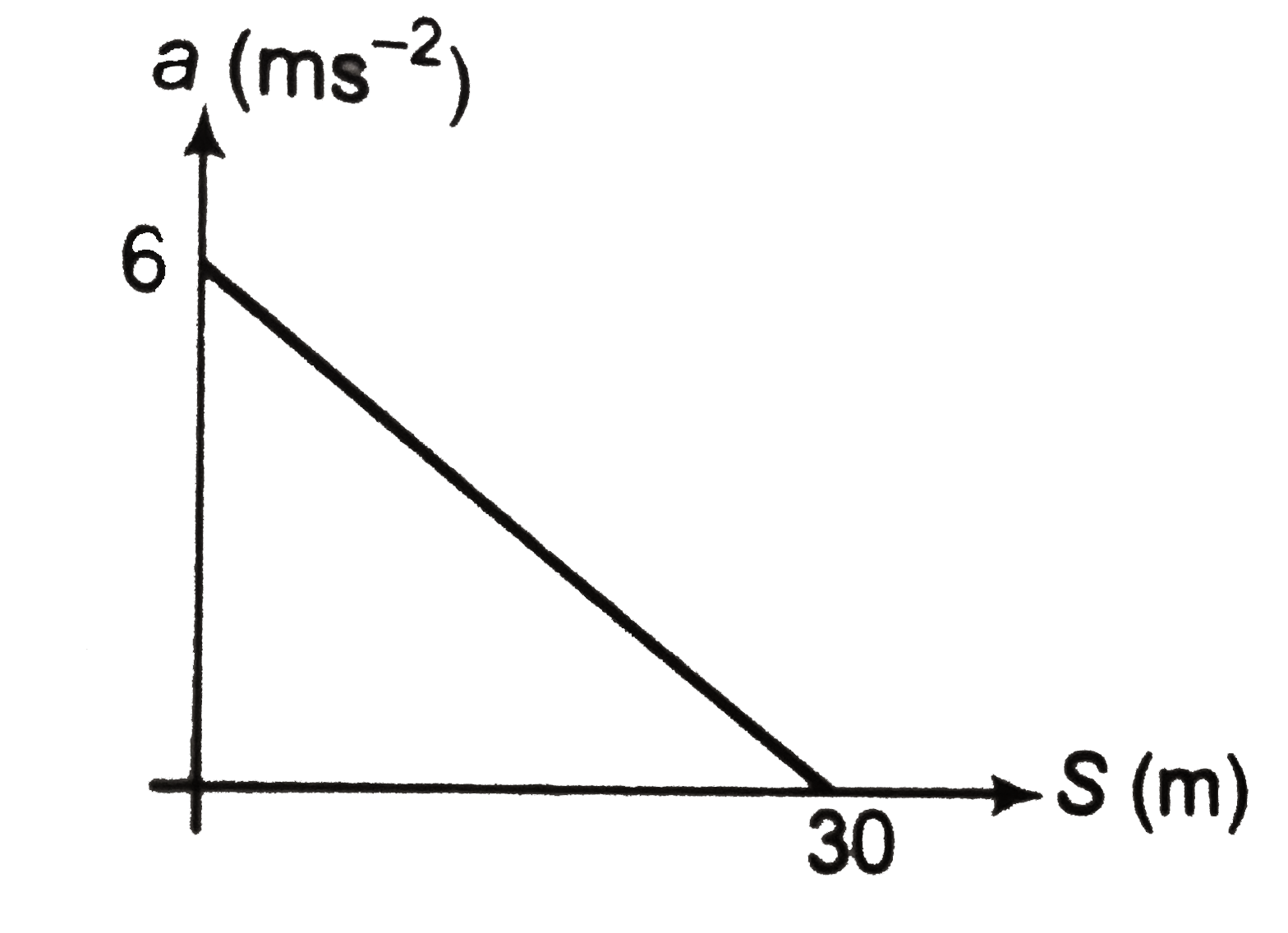
A street car moves rectilinearly from station A to the next station B (from rest to rest) with an acceleration varying according to the law f=a−bx, where a and b are constants and x is the distance from station A. The distance between the two stations and the maximum velocity areView SolutionQuestion 140
Two particles are moving along two long straight lines, in the same plane with same speed equal to 20cm/s. The angle between the two linse is 60∘ and their intersection point isO. At a certain moment, the two particles are located at distances 3m and 4m from O and are moving twowards O. Subsequently, the shortest distance between them will beView SolutionQuestion 145
Starting from rest a particle is first accelerated for time t1 with constant acceleration a1 and then stops in time t2 with constant retardation a2. Let v1 be the average velocity in this case and s1 the total displacement. In the second case it is accelerating for the same time t1 with constant acceleration 2a1 and come to rest with constant retardation a2 in time t3. If v2 is the average velocity in this case and s2 the total displacement, thenView SolutionQuestion 156
An elevator without a ceiling is ascending up with an acceleration of 5ms−2. A boy on the elevator shoots a ball in vertical upward direction from a height of 2 m above the floor of elevator. At this instant the elevator is moving up with a velocity of 10ms−1 and floor of the elevator is at a height of 50 m from the ground. The initial speed of the ball is 15ms−1 with respect to the elevator. Consider the duration for which the ball strikes the floor of elevator in answering following questions. (g=10ms−2)
1. The time in which the ball strikes the floor of elevator is given byView SolutionQuestion 157
An elevator without a ceiling is ascending up with an acceleration of 5ms−2. A boy on the elevator shoots a ball in vertical upward direction from a height of 2 m above the floor of elevator. At this instant the elevator is moving up with a velocity of 10ms−1 and floor of the elevator is at a height of 50 m from the ground. The initial speed of the ball is 15ms−1 with respect to the elevator. Consider the duration for which the ball strikes the floor of elevator in answering following questions. (g=10ms−2)
2. The maximum height reached by ball, as measured from the ground would beView SolutionQuestion 158
An elevator without a ceiling is ascending up with an acceleration of 5ms−2. A boy on the elevator shoots a ball in vertical upward direction from a height of 2 m above the floor of elevator. At this instant the elevator is moving up with a velocity of 10ms−1 and floor of the elevator is at a height of 50 m from the ground. The initial speed of the ball is 15ms−1 with respect to the elevator. Consider the duration for which the ball strikes the floor of elevator in answering following questions. (g=10ms−2)
3. Displacement of ball with respect to ground during its night would beView SolutionQuestion 159
An elevator without a ceiling is ascending up with an acceleration of 5ms−2. A boy on the elevator shoots a ball in vertical upward direction from a height of 2 m above the floor of elevator. At this instant the elevator is moving up with a velocity of 10ms−1 and floor of the elevator is at a height of 50 m from the ground. The initial speed of the ball is 15ms−1 with respect to the elevator. Consider the duration for which the ball strikes the floor of elevator in answering following questions. (g=10ms−2)
4. The maximum separation between the floor of elevator and the ball during its flight would beView SolutionQuestion 160
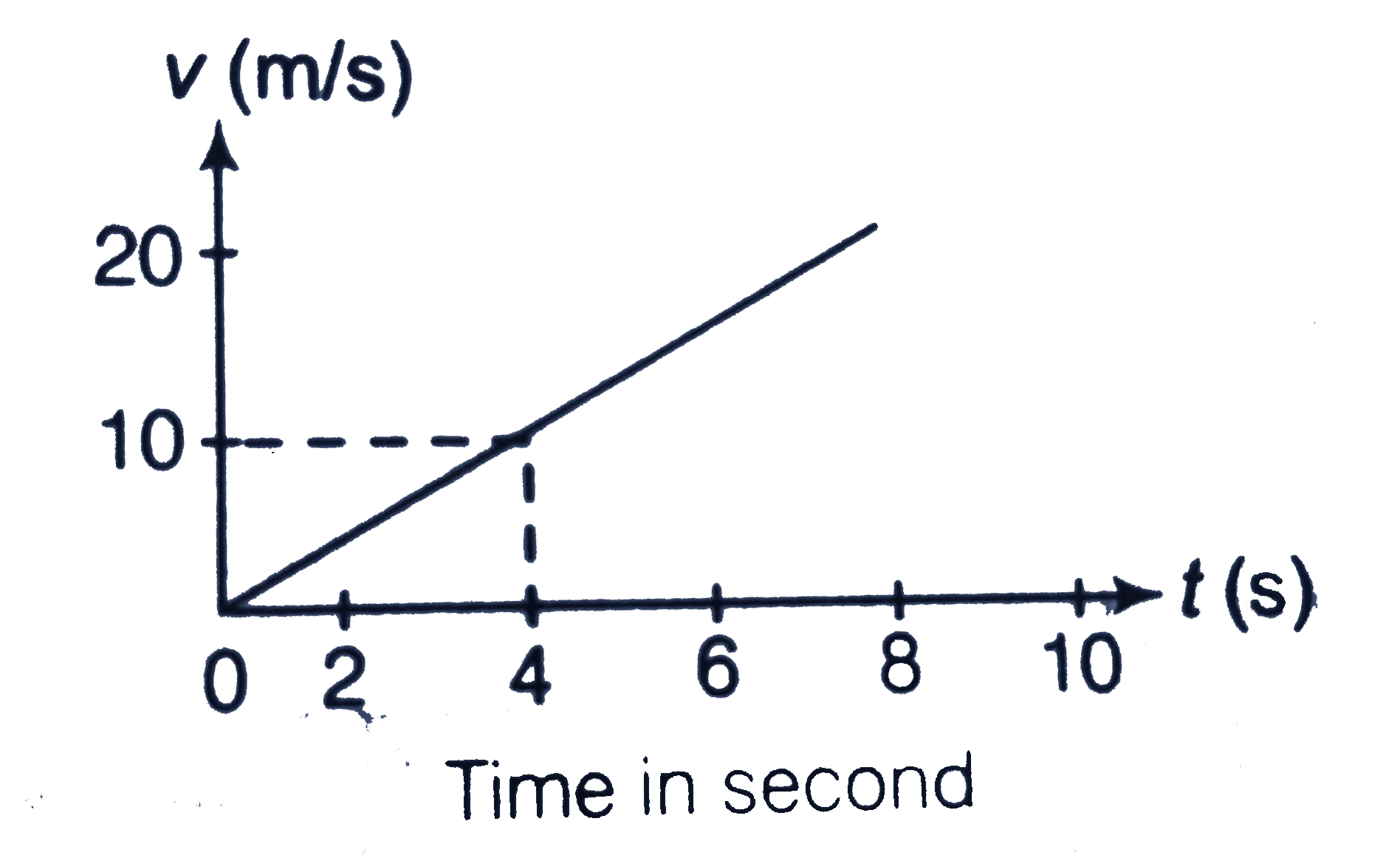
A situation is shown in which two objects A and B start their motion from same point in same direction. The graph of their velocities against time is drawn. uAanduB are the initial velocities of A and B respectively. T is the time at which their velocities become equal after start of motion. You cannot use the data of one question while solving another question of the same set. So all the questions are independent of each other.
5. If the value of T is 4 s, then the time after which A will meet B is
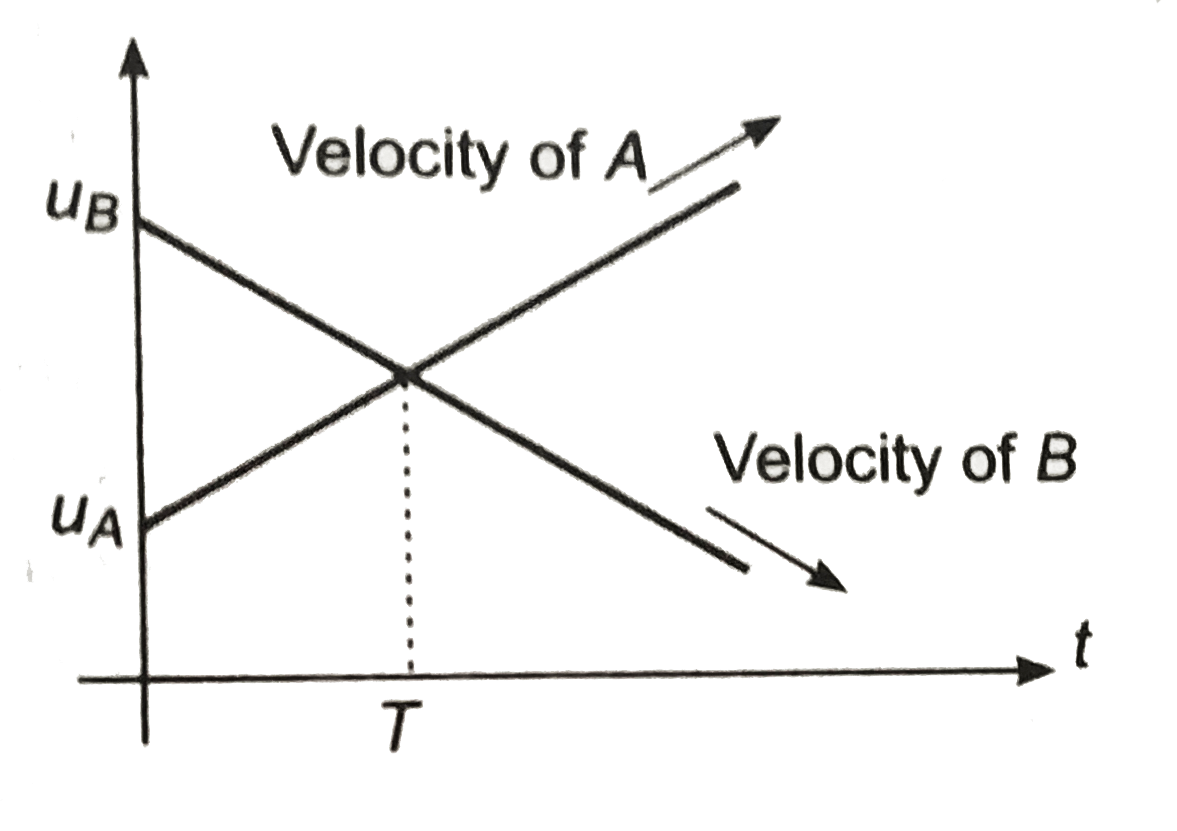View SolutionQuestion 161
A situation is shown in which two objects A and B start their motion from same point in same direction. The graph of their velocities against time is drawn. uAanduB are the initial velocities of A and B respectively. T is the time at which their velocities become equal after start of motion. You cannot use the data of one question while solving another question of the same set. So all the questions are independent of each other.
6. Let vAandvB be the velocities of the particles A and B respectively at the moment A and B meet after start of the motion. If uA=5ms−1anduB=15ms−1, then the magnitude of the difference of velocities vAandvB is
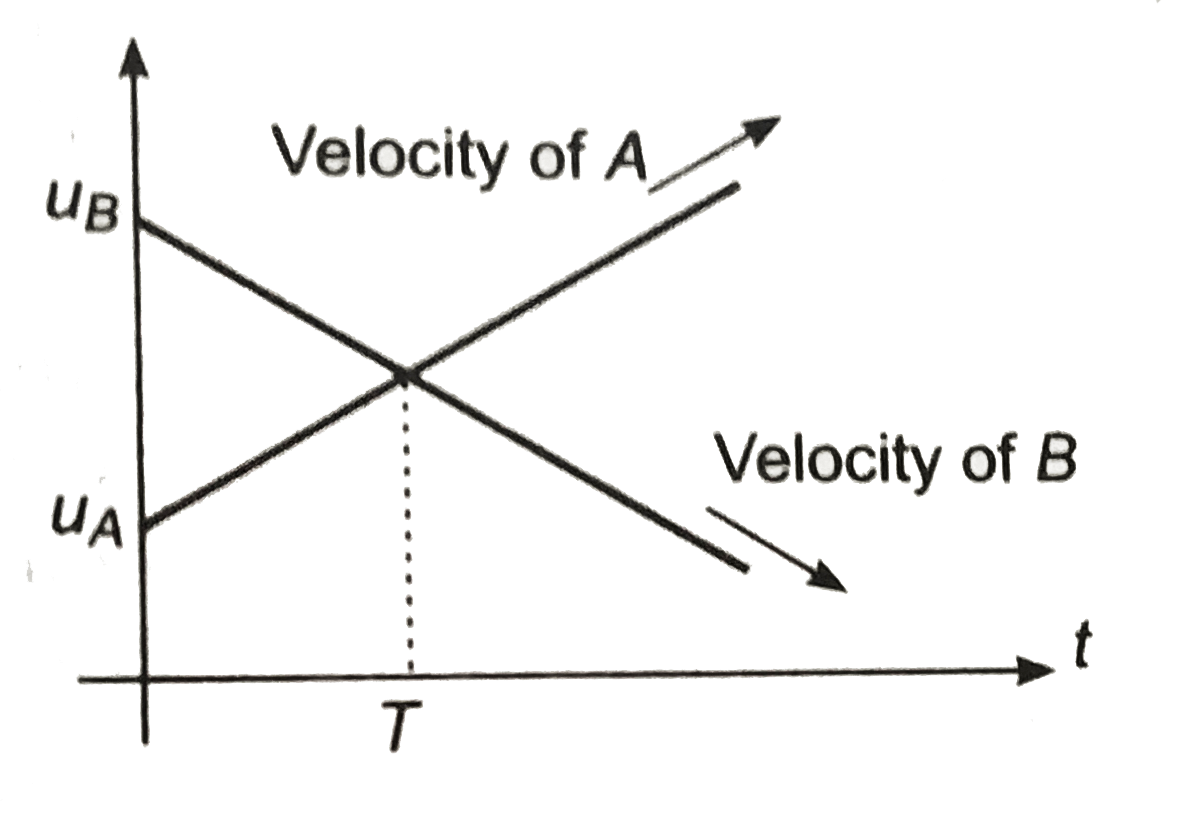View SolutionQuestion 162
A situation is shown in which two objects A and B start their motion from same point in same direction. The graph of their velocities against time is drawn. uAanduB are the initial velocities of A and B respectively. T is the time at which their velocities become equal after start of motion. You cannot use the data of one question while solving another question of the same set. So all the questions are independent of each other.
7. After 10 s of the start of motion of both objects A and B, find the value of velocity of A if uA=6ms−1,uB=12ms−1 and at T velocity of A is 8ms−1andT=4s
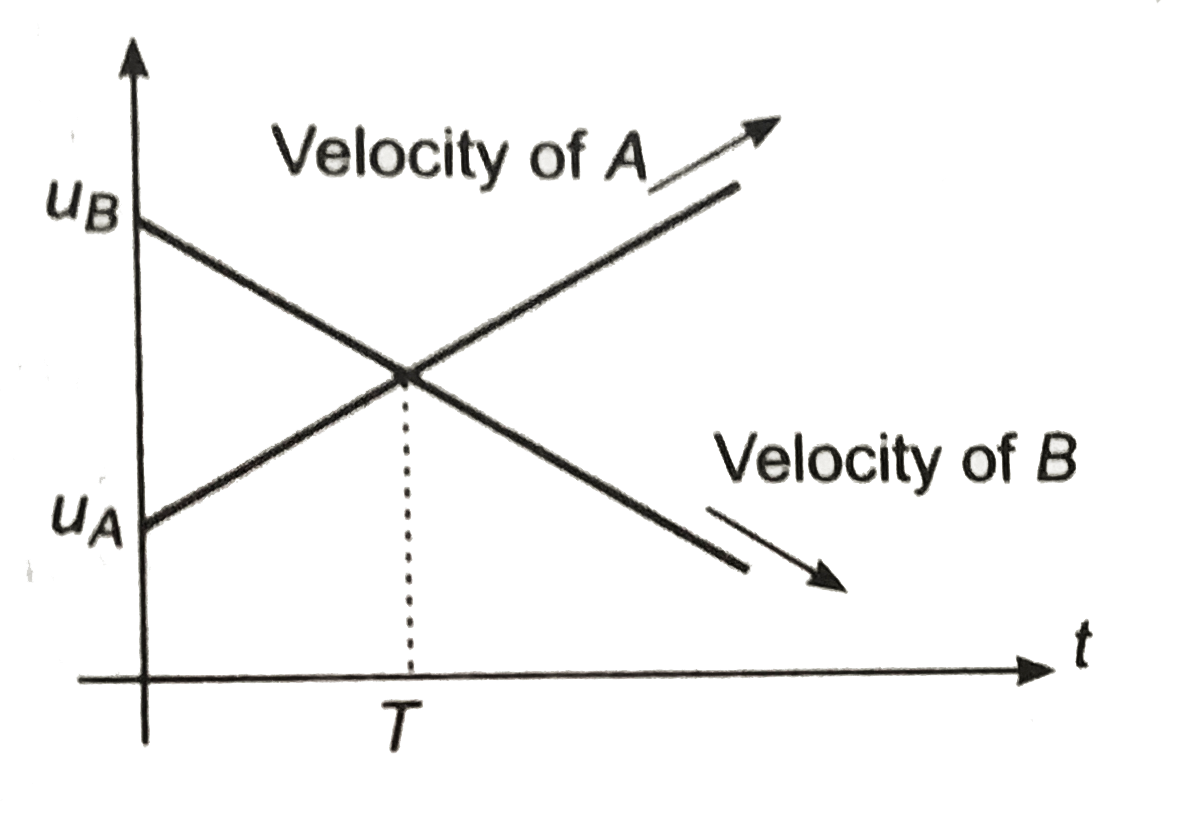View SolutionQuestion 165
At the initial moment three points A, B and C are on a horizontal straight line at equal distances from one another. Point A begins to move vertically upward with a constant velocity v and point C vertically downward without any initial velocity but with a constant acceleration a. How should point B move vertically for all the three points to be constantly on one straight line. The points begin to move simultaneously.View SolutionQuestion 167
A car is to be hoisted by elevator to the fourth floor of a parking garage, which is 14 m above the ground. If the elevator can have maximum acceleration of 0.2m/s2 and maximum deceleration of 0.1m/s2 and can reach a maximum speed of 2.5 m//s, determine the shortest time to make the lift, starting from rest and ending at rest.View SolutionQuestion 168
To stop a car, first you require a certain reaction time to begin braking, then the car slows under the constant braking deceleration. Suppose that the total distance moved by your car during these two phases is 56.7 m when its initial Speed is 80.5 km//h and 24.4 m when its initial speed in 48.3 km//h. What are
(a) your reaction time and
(b) the magnitude or the deceleration?View SolutionQuestion 169
An elevator without a ceiling is ascending with a constant speed of 10 m//s. A boy on the elevator shoots a ball directly upward, from a height of 2.0 m above the elevator floor. At this time the elevator floor is 28 m above the ground. The initial speed of the ball with respect to the elevator is 20 m//s. (Take g=9.8m/s2)
(a) What maximum height above the ground does the ball reach?
(b) How long does the ball take to return to the elevator floor?View SolutionQuestion 172
A man wishes to cross a river of width 120 m by a motorboat. His rowing speed in still water is 3m/s and his maximum walking speed is 1m/s. The river flows with velocity of 4m/s.
(a) Find the path which he should take to get to the point directly opposite to his starting point in the shortest time.
(b) Also, find the time which he takes to reach his destination.View SolutionQuestion 173
The current velocity of river grows in proportion to the distance from its bank and reaches the maximum value v0 in the middle. Near the banks the velocity is zero. A boat is moving along the river in such a manner that the boatman rows his boat always perpendicular to the current. The speed of the boat in still water is u. Find the distance through which the boat crossing the river will be carried away by the current, if the width of the river is c. Also determine the trajectory of the boat.View SolutionQuestion 175
A river of width a with straight parallel banks flows due north with speed u. The points O and A are on opposite banks and A is due east of O. Coordinate axes Ox and Oy are taken in the east and north directions respectively. A boat, whose speed is v relative to water, starts from O and crosses the river. If the boat is steered due east and u varies with xas:u=x(a−x)va2. Find
(a) equation of trajectory of the boat,
(b) time taken to cross the river,
(c) absolute velocity of boatman when he reaches the opposite bank,
(d) the displacement of boatman when he reaches the opposite bank from the initial position.View SolutionQuestion 176
A river of width ω is flowing with a uniform velocity v. A boat starts moving from point P also With velocity v relative to the river. The direction of resultant velocity is always perpendicular to the line joining boat and the fixed point R. Point Q is on the opposite side of the river. P, Q and R are in a straight line. If PQ=QR=ω, find (a) the trajectory of the boat, (b) the drifting of the boat and (c) the time taken by the boat to cross the river.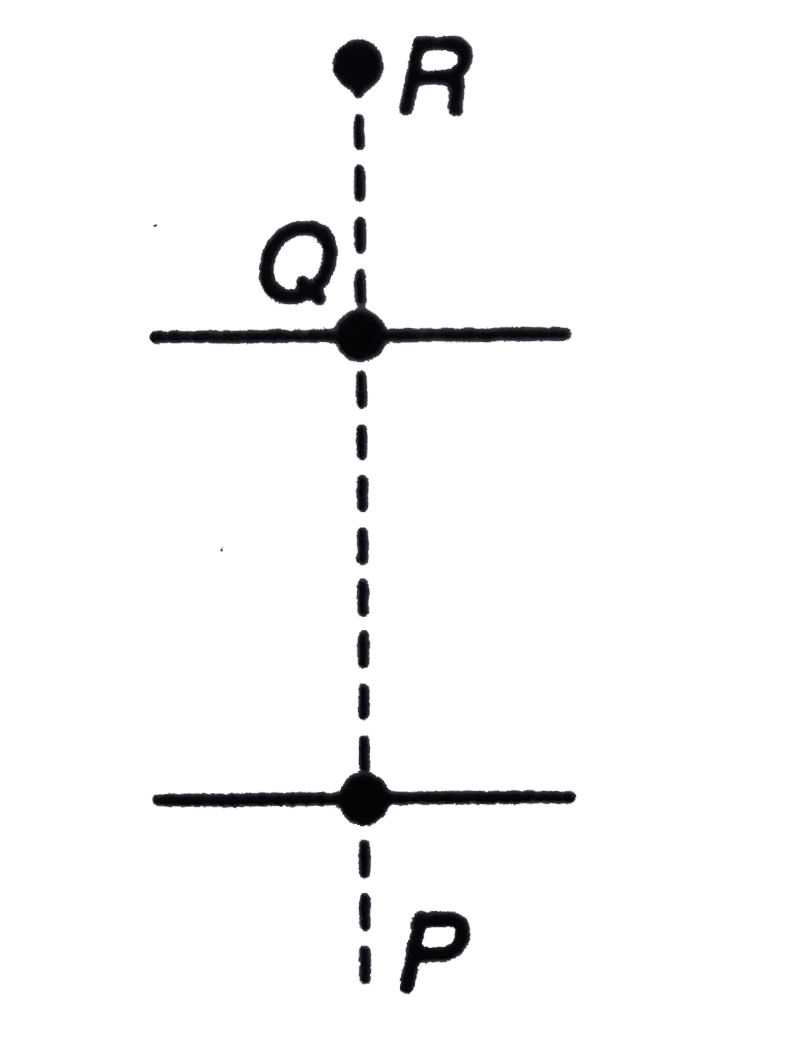
View SolutionQuestion 180
The Speed Of a particle moving in a plane is equal to the magnitude of its instantaneous velocity, v=∣vl=√v2x+v2y.
(a) Show that the rate of change of the speed is dvdt=vxax+vyay√v2x+v2y.
(b) Show that the rate of change of speed can be expressed as dvdt is equal toat the component of a that is parallelto v.View SolutionQuestion 181
A man with some passengers in his boat, starts perpendicular to flow of river 200 m wide and flowing with 2m/s. Speed of boat in still water is 4m/s. When he reaches half the width of river the passengers asked him that they want to reach the just opposite end from where they have started.
(a) Find the direction due which he must row to reach the required end.
(b) How many times more time, it would take to that if he would have denied the passengers?View SolutionQuestion 182
A child in danger of drowning in a river is being carried downstream by a current that flows uniformly at a speed of 2.5km/h. The child is 0.6 km from shore and 0.8 km upstream of a boat landing when a rescue boat sets out. If the boat proceeds at its maximum speed of 20km/h with respect to the water, what angle does the boat velocity v make with the shore? How long will it take boat to reach the child?View SolutionQuestion 183
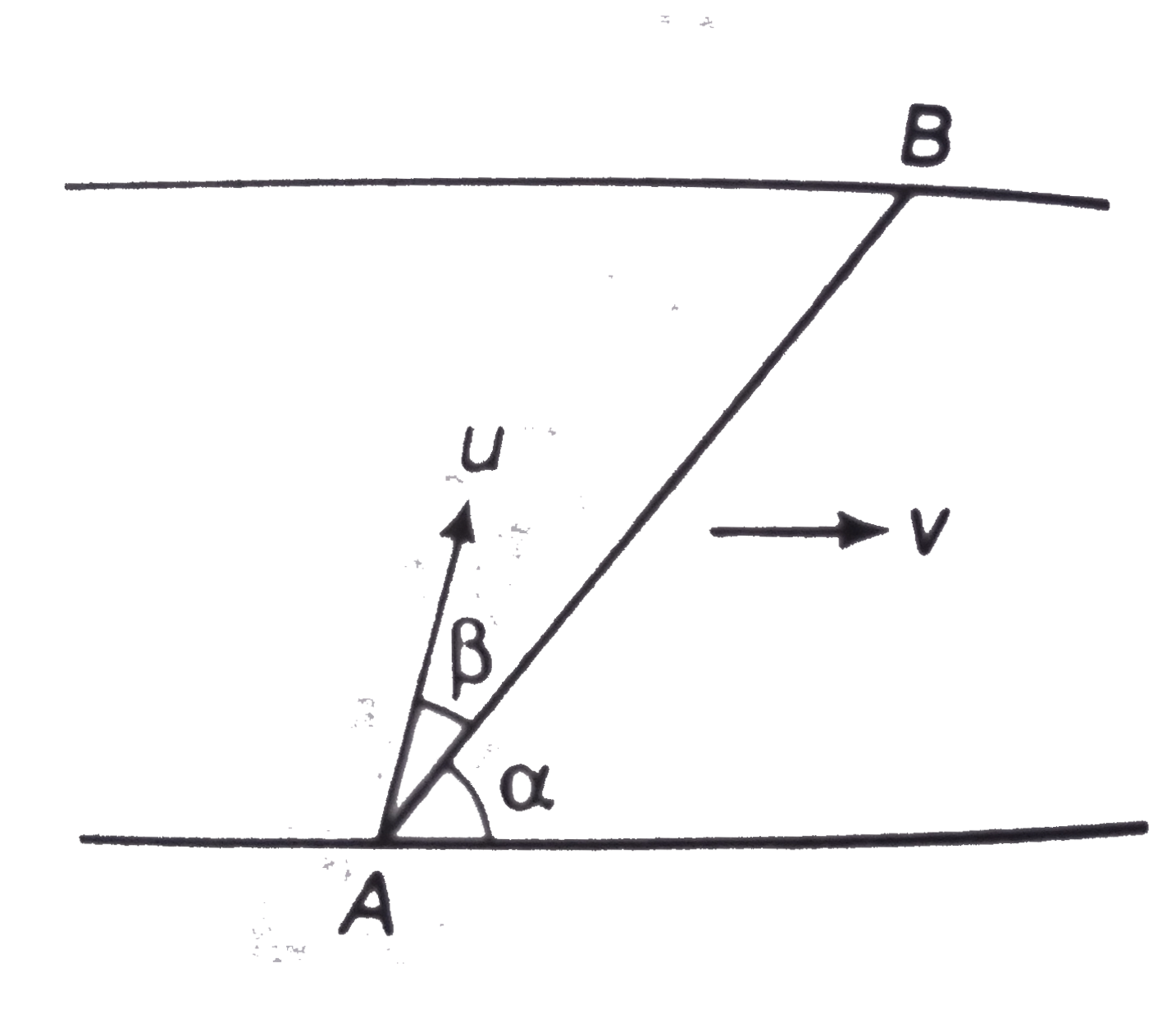
A launch plies between two points A and B on the opposite banks of a river always following the line AB. The distance S between points and B is 1200 m. The velocity of the river current v=1.9m/s is constant over the entire width of the river. The line AB makes an angle α=60∘ with the direction of the current. With what velocity u and at what angle beta to the line AB should the launch move to cover the distance AB and back in a time t=5min? The angle beta remains the same during the passage from A to B and from B to A.
View SolutionQuestion 184
The slopes of wind screen of two cars are α1=30∘andα2=15∘ respectively. At what ratio v1v2 of the velocities of the cars will their drivers see the hail stones bounced back by the wind screen on their cars in vertical direction? Assume hail stones fall vertically downwards and collisions to be elastic.View SolutionQuestion 185
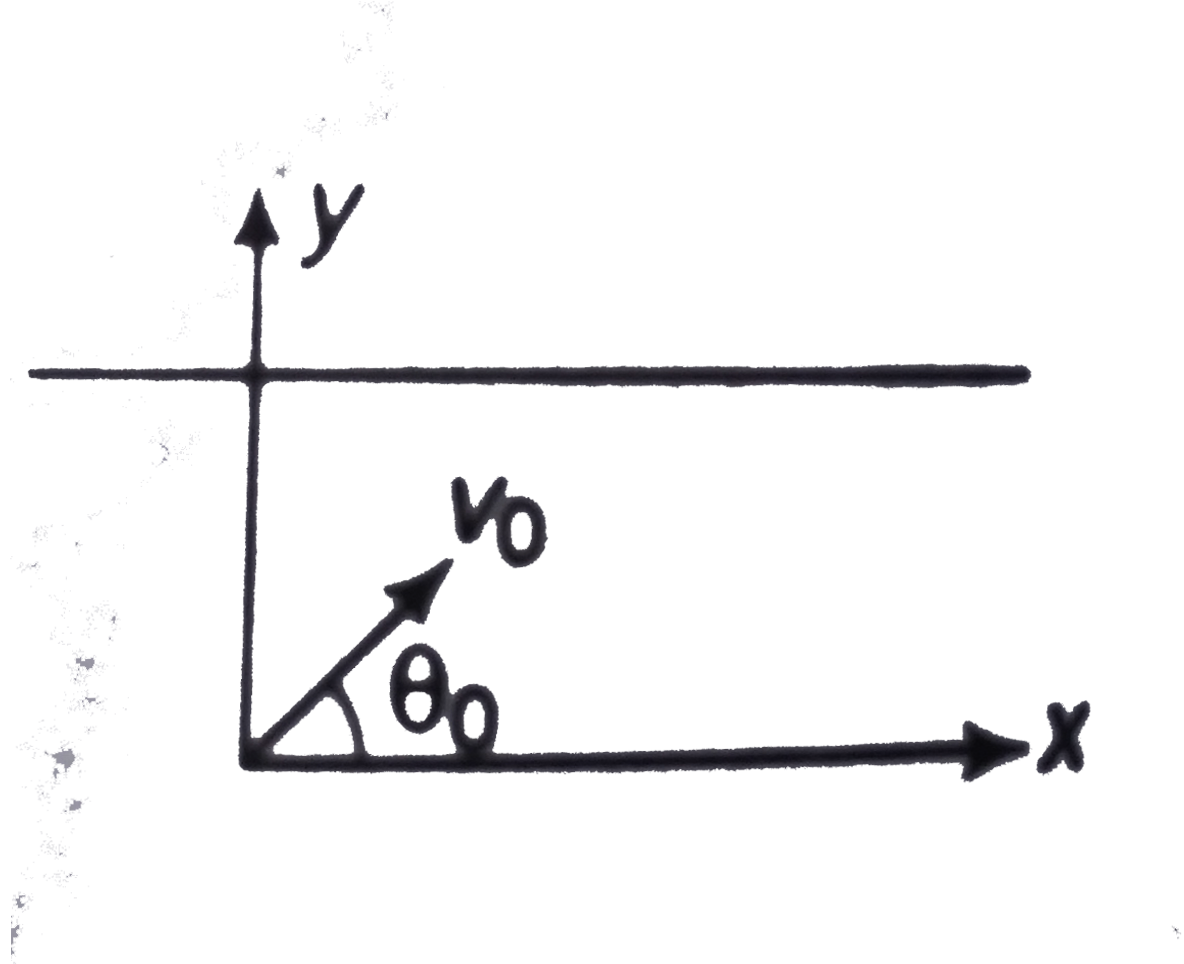
A projectile of mass m is fired into a liquid at an angle θ0 with an initial velocity v0 as shown. If the liquid develops a frictional or drag resistance on the projectile which is proportional to its velocity, i. e. F=−kv where k is a positive constant, determine the x and y components of its velocity at any instant. Also find the maximum distance xmax that it travels?
View SolutionQuestion 186
A man in a boat crosses a river from point A. If he rows perpendicular to the banks he reaches point C (BC=120m) in 10 min. If the man heads at a certain angle α to the straight line AB (AB is perpendicular to the banks) against the current he reaches point B in 12.5 min. Find the width of the river w, the rowing velocity u, the speed of the river current v and the angle α. Assume the velocity of the boat relative to water to be constant and the same magnitude in both cases.
View Solution
All Exercises from DC PANDEY ENGLISH Class 11 PHYSICS KINEMATICS
- ASSERTION AND REASON
- COMPREHENSION
- EXERCISE 6.1
- EXERCISE 6.2
- EXERCISE 6.3
- EXERCISE 6.4
- EXERCISE 6.5
- EXERCISE 6.6
- EXERCISE 6.7
- EXERCISE 6.8
- EXERCISE 6.9
- MORE THAN ONE CORRECT
- OBJECTIVE
- SUBJECTIVE
- SUBJECTIVE QUESTIONS
- COMPREHENSION_TYPE
- EXAMPLE
- EXAMPLE TYPE 1
- EXAMPLE TYPE 2
- EXAMPLE TYPE 3
- EXAMPLE TYPE 4
- EXAMPLE TYPE 5
- EXAMPLE TYPE 6
- EXAMPLE TYPE 7
- INTEGER_TYPE
- MATCH THE COLUMN
- MCQ_TYPE
- MISCELLANEOUS EXAMPLE
- SCQ_TYPE