Illustration from CENGAGE PHYSICS (HINGLISH) KINEMATICS-2 for Class 11
| Class 11 | PHYSICS |
| Chapter | KINEMATICS-2 |
| CENGAGE PHYSICS (HINGLISH) | Illustration |
| Medium | English |
| Academic Year | 2023-2024 |
Question 5
A batsman hits a ball at an angle of 30∘ with an initial speed of 30ms−1. Assuming that the ball travels in a vertical plane, calculate.
(a) The time at which the ball reaches the highest point.
(b) The maximum height reached.
( c) The horizontal range of the ball.
(d) The time for which the ball is in the air.View SolutionQuestion 9
Four cannon balls, (1),(2),(3),and(4) are fired from level ground. Cannon ball (1) is fired at an angle of 60∘ above the horizontal and follows the path shown in (Fig. 5.9).
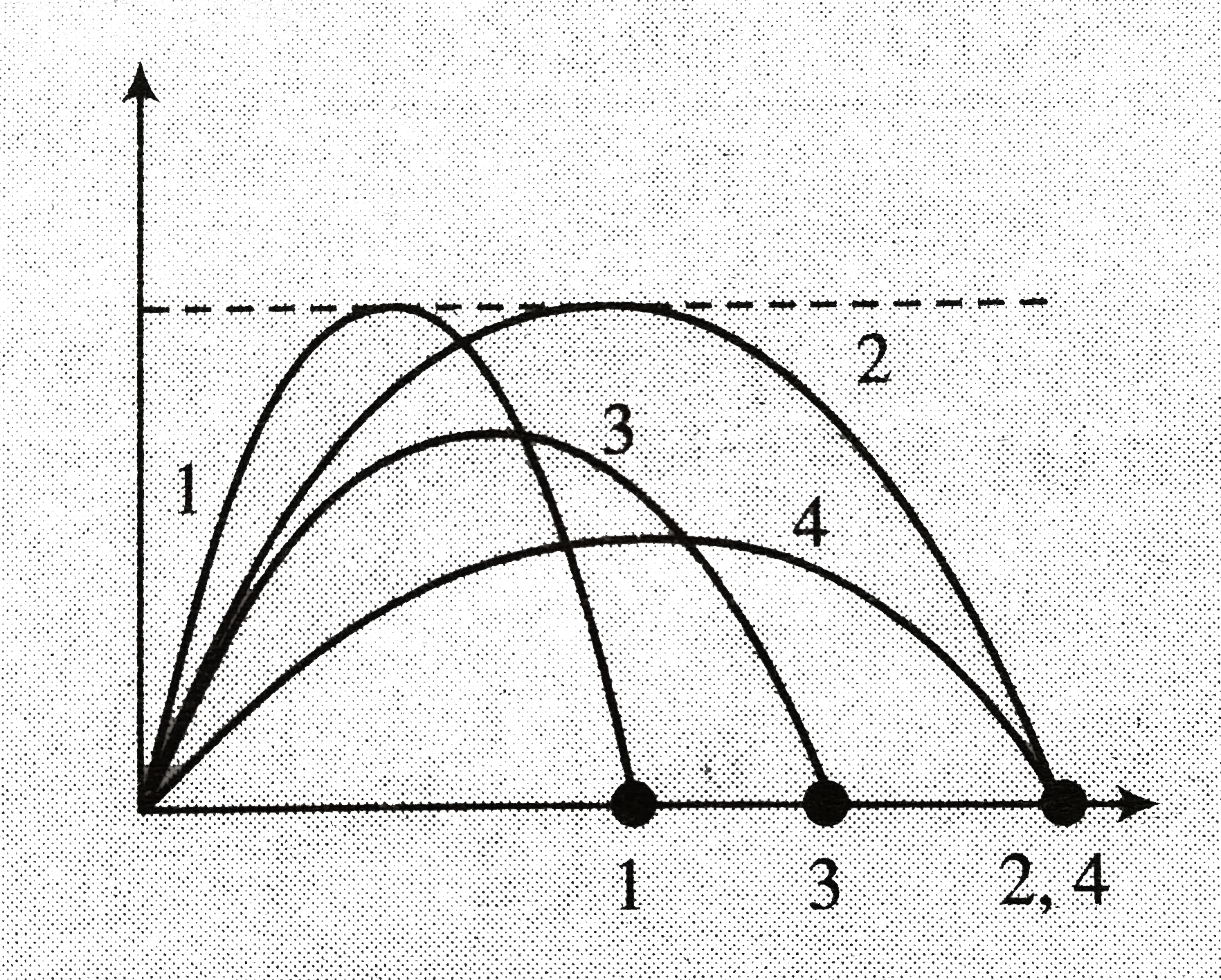 .
.
Cannon balls (2) and (3) are fired at angle of 45∘ and (4) is fired at an angle of 30∘ above the horizontal. Which cannon ball has the largest initial speed ? View SolutionQuestion 10
Two graphs of the same projectile motion (in the x - y plane) projected from origin are shown in (Fig. 5 .10). X - axis is along horozontal direction and Y - axis is vertically upwards. Take g=10ms2
Find (i) The y component of initial velocity and
(ii) the X component of initial velocity.
 .View Solution
.View SolutionQuestion 13
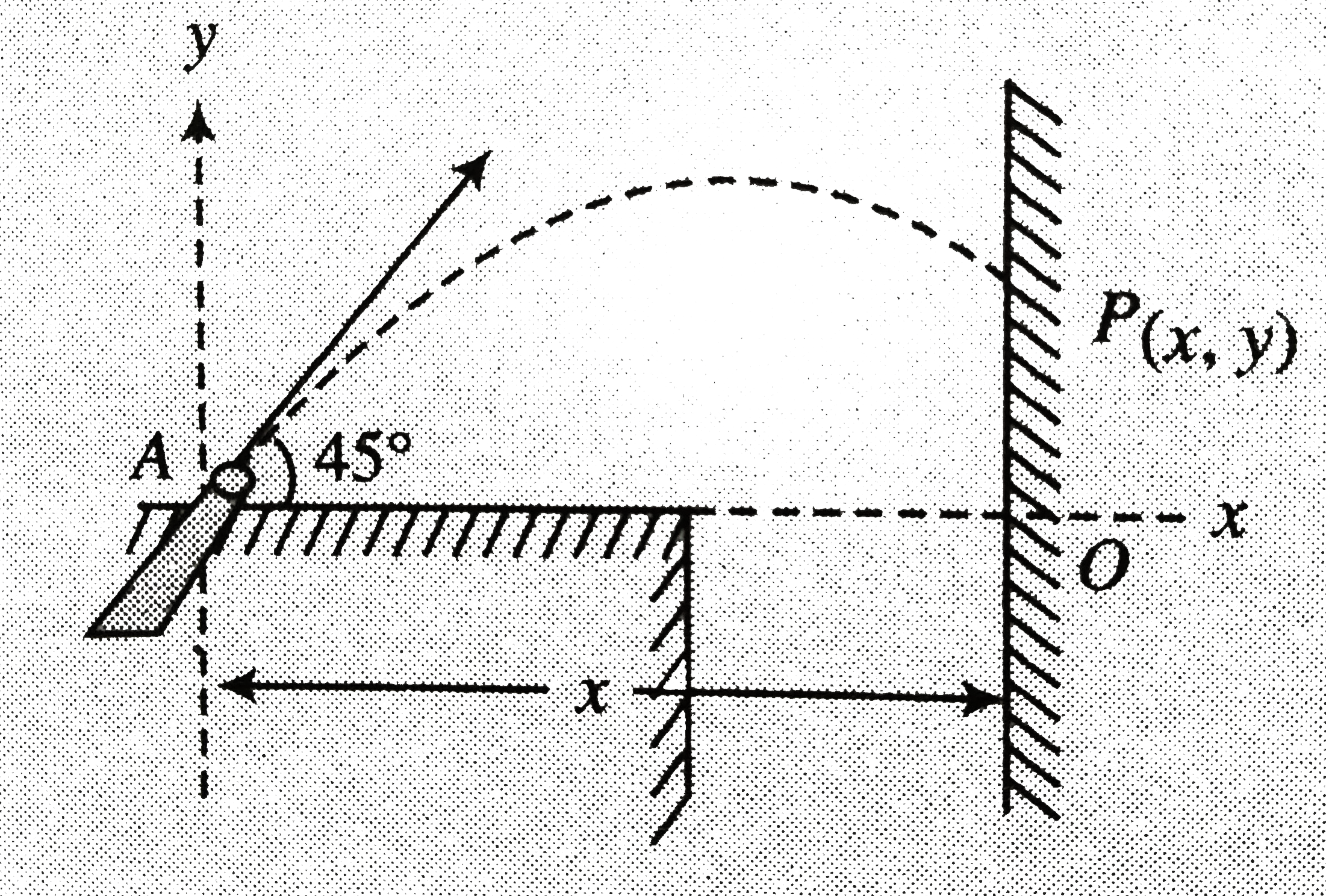
A particle is projected from the ground at t=0 so that on its way it just clears two vertical walls of equal height on the ground. The particle was projected with initial velocity u and at angle θ with the horiozontal. If the particle passes just grazing top of the wall at time t=t1andt=t2, then calculate.
(a) the height of the wall.
(b) the time t1andt2 in terms of height of the wall.
Write the expression for calculating the range of this projectile and separation between the walls.View SolutionQuestion 16
A particle projected atv a definite angle ∝ to the horizontal passes through points (a,b)and(b,a), referred to horizontal and vertical axes through the points of projection. Show that :
(a) The horizontal range R=a2+ab+b2a+b .
(b) The angle of projection ∝ is given by
tan−1[a2+ab+b2ab].View SolutionQuestion 19
A relief food package is dropped from a airplane which is moving horizontal with a velocity of 30ms−1 at a height h=50m. Find the (a) time of flight of the package, (b) location of the point of striking of the food package, (c ) velocity of the package at the time of striking the ground, and (d) displacement of the food package.
 .View Solution
.View SolutionQuestion 21
A boy of height 1.5m, making move on a skateboard due east with velocity 4ms−1, throws a coin vertically up a velocity of 3ms−1 relative to himself.
(a) Find the total displacement of the coin relative to ground till it comes to the hand of the boy.
(b) What isthe maximum height attained by the coin w.r.t. to ground ?View SolutionQuestion 22
A shell is projected from a gun with a muzzle velocity, u. The gun is fitted with a trolly car at an angle θ as shown in (Fig. 5.33). If the trolley car is made to move with constant velocity v towards right, find the
(a) horizontal range of the shell relative to ground.
(b) horizontal range of the shell relative to a person travelling with trolley.
 .View Solution
.View SolutionQuestion 23
A man is standing on a rail road car travelling with a constant speed of v=10ms−1 (Fig . 5.34). He wishes to throw a ball through a stationary hoop 5m above the height of his hands in such a manner that the ball will move horizontally as it passes through the hoop. He throws the ball with a speed of 12.5ms−1 w.r.t. himself.
(a) What must be the vertical component of the initial velocity of the ball ?
(b) How many seconds after he releases the ball will it pass through the hoop ?
( c) At what horizontal distance in front of the loop must he release the ball ?
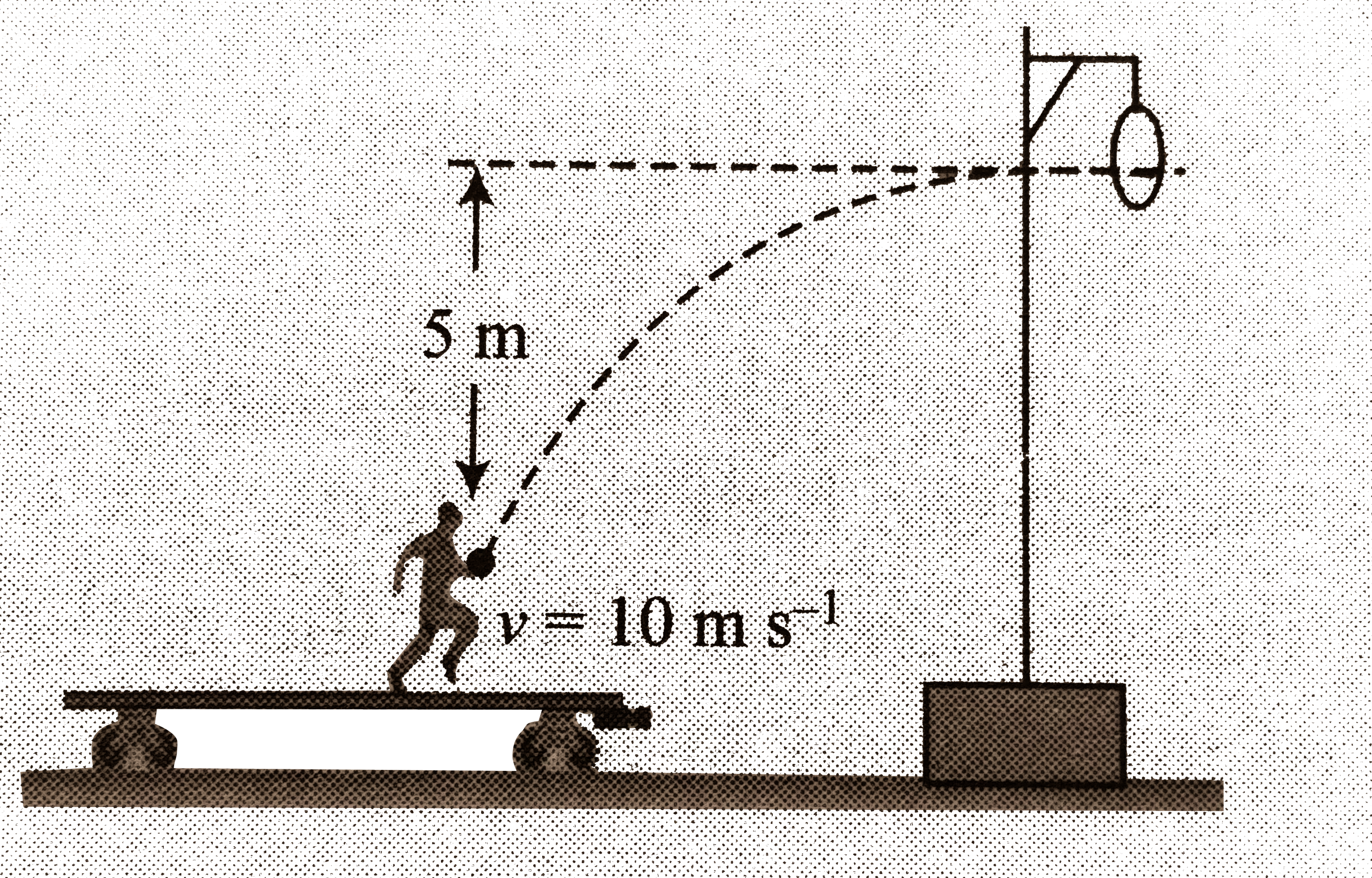 .View Solution
.View SolutionQuestion 24
A man is riding on a flat car travelling with a constant speed of 10m/s.He wishes to throw a ball through a stationary hoop 15m above the height of his hands in such a manner that the ball will move horizontally as it passes through the hoop. He throws the ball with a speed of 12.5m/s w.r.t himself.
At what horizontal distance in front of the hoop must he release the ball?View SolutionQuestion 26
Two inclined planes OA and OB having inclinations 30∘ and 60∘ with the horizontal respectively intersect each other at O, as shown in figure. A particle is projected from point P with velocity u=10√3m/s along a direction perpendicular to plane OA. If the particle strikes plane OB perpendicular at Q. Calculate.
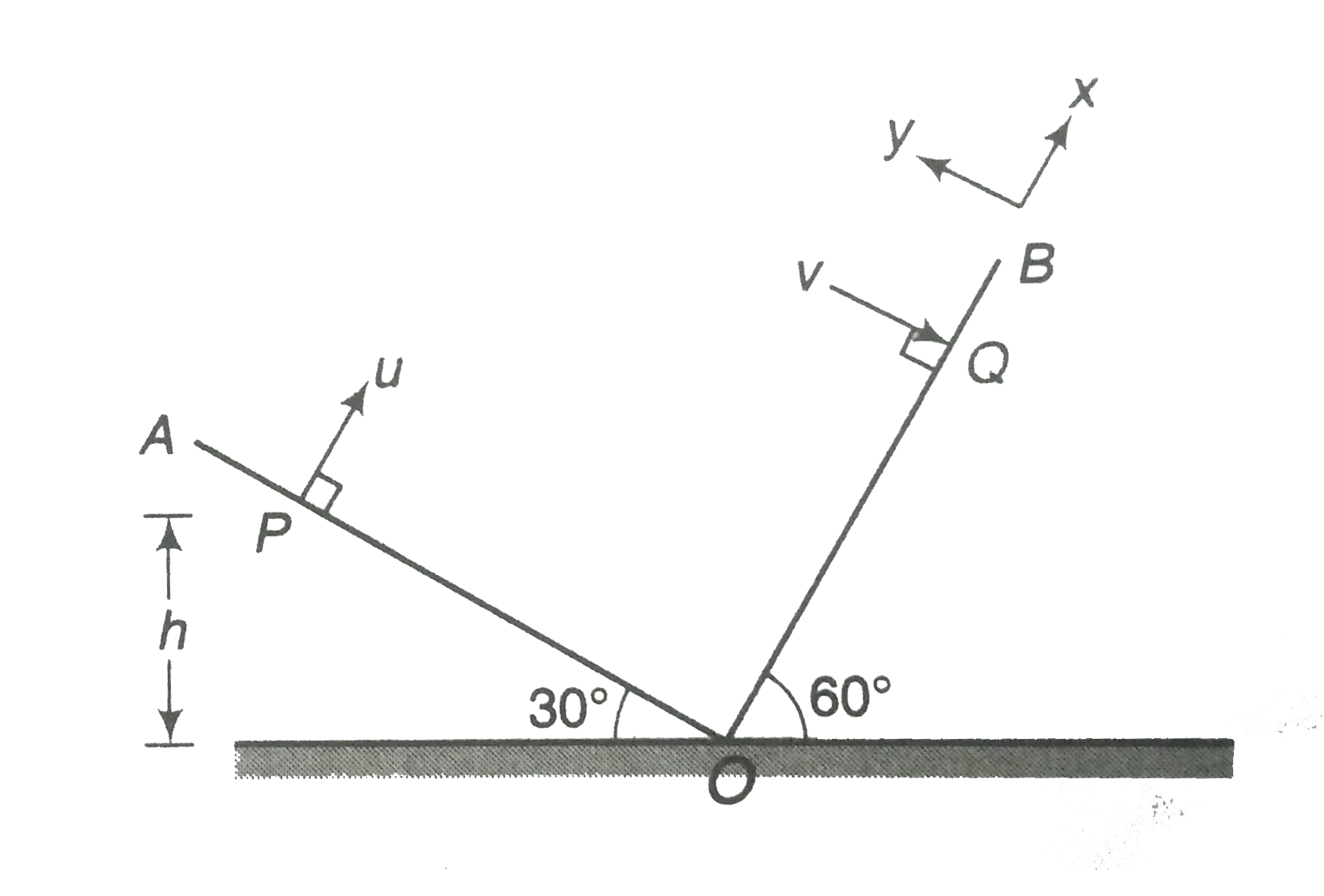
(a) time of flight,
(b) velocity with which the particle strikes the plane OB,
(c) height h of point P from point O,
(d) distance PQ. (Take g=10m/s2)View SolutionQuestion 27
A truck starts from origin, accelerating with ams−2 in positive x - axis direction. After 2s, a man standing at the starting point of the truck projected a ball at an angle 30∘ with velocity vms−1. Find the relation between aandv such that the ball hits the truck. (Assume that truck is moving on horizontal plane and the man projected the ball from the same horizontal level of truck).View SolutionQuestion 32
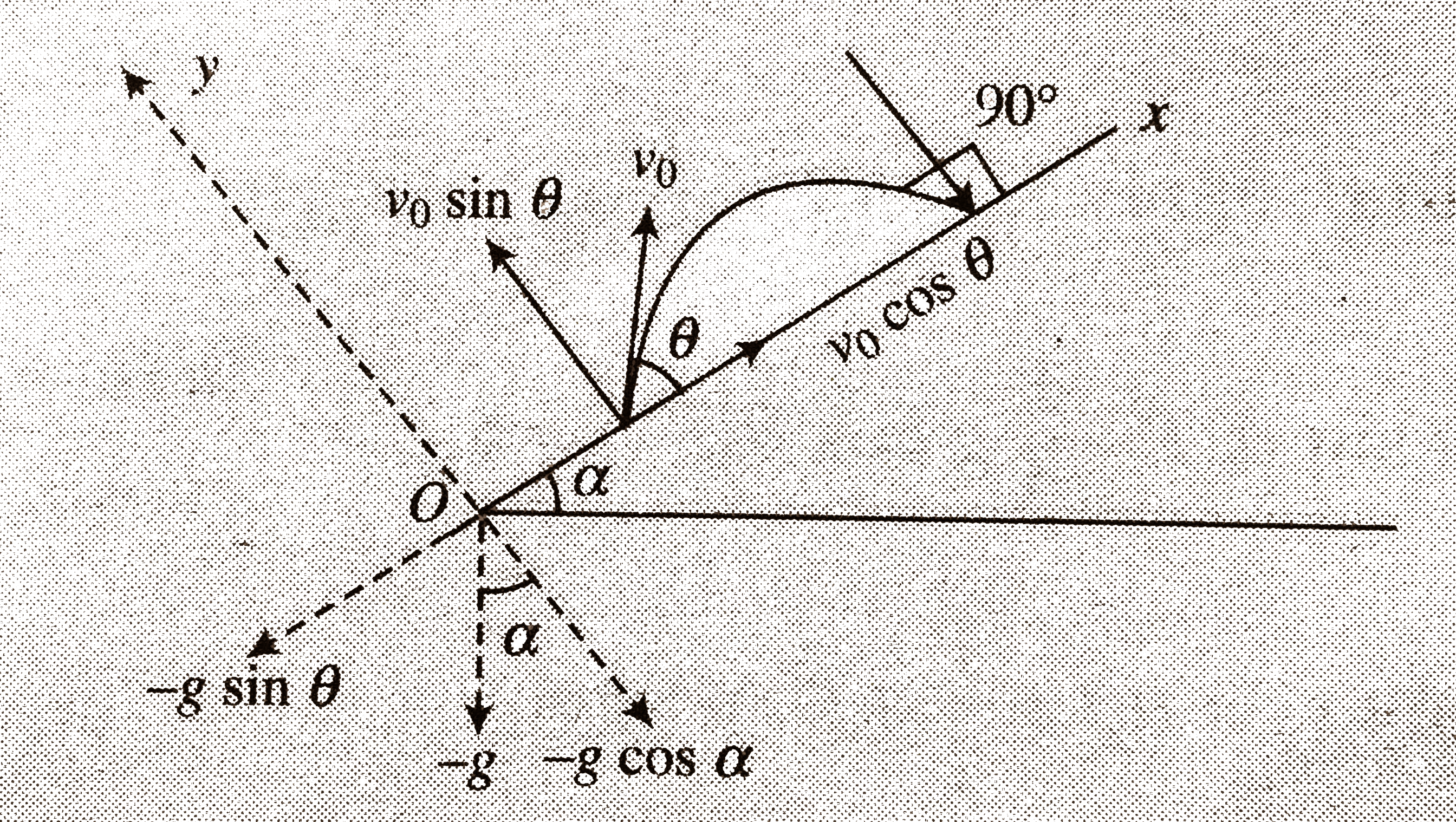
An inclined plane makes an angle θ0=30∘ with the horizontal. A particle is projected from this plane with a speed of 5ms−1 at an angle of elevation β=30∘ with the horizontal as shown in (Fig. 5.53).
(a) Find the range of the particle on the plane when it strikes the plane.
(b) Find the range of the particle for β=120∘.
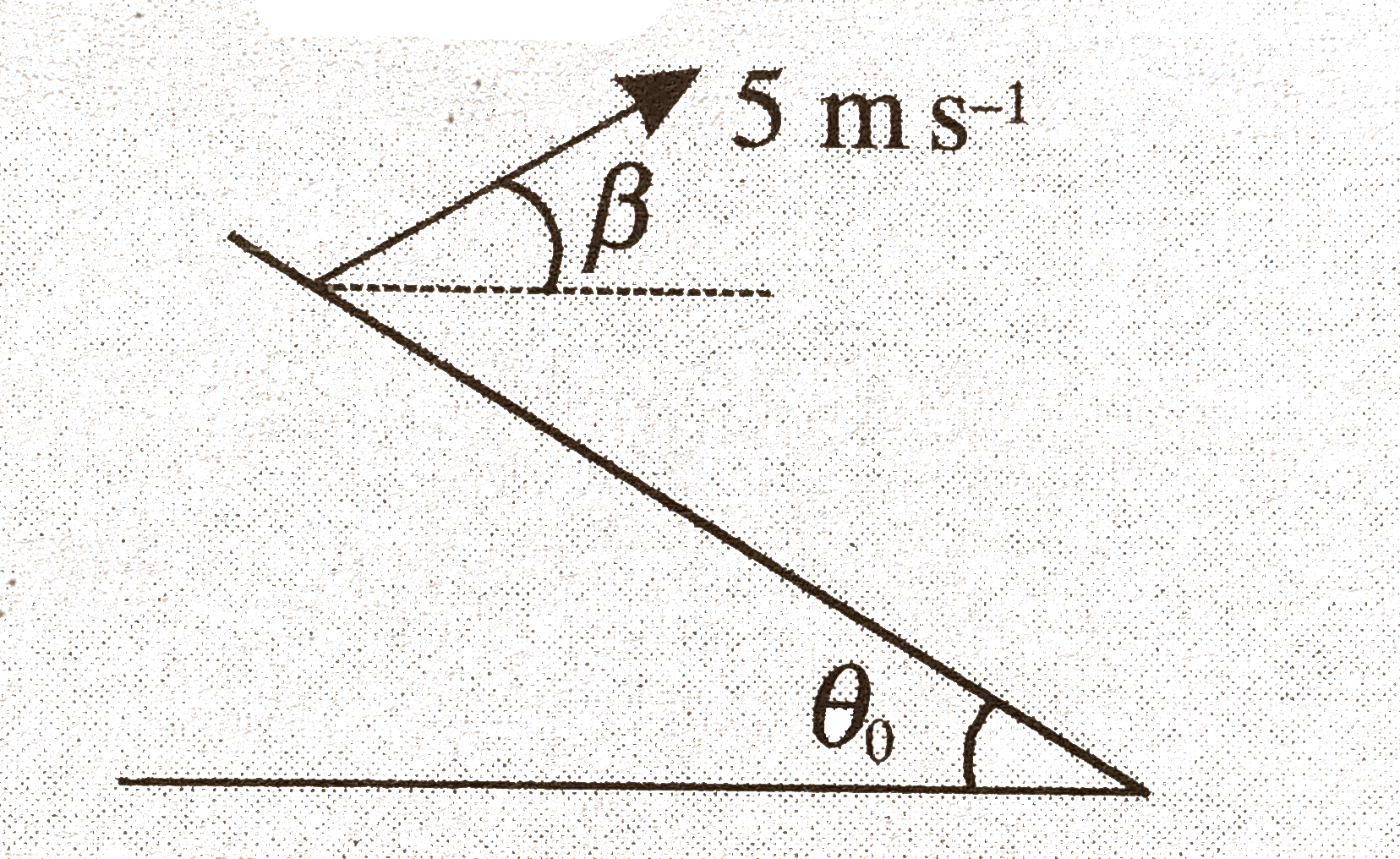 .View Solution
.View SolutionQuestion 33
A body has maximum range R1 when projected up the plane. The same body when projected down the inclined plane, it has maximum range R2. Find the maximum horizontal range. Assume equal speed of projection in each case and the body is projected onto the inclined plane in the line of the greatest slope.View SolutionQuestion 35
Two roads one , along the y - axis and another along a direction at angle θ with x - axis, are as shown in (Fig. 5.68). Two cars AandB are moving along the roads. Considerthe situation of the diagram. Draw the direction of
(a) Car B as seen from car A.
(b) Car A as seen car B.
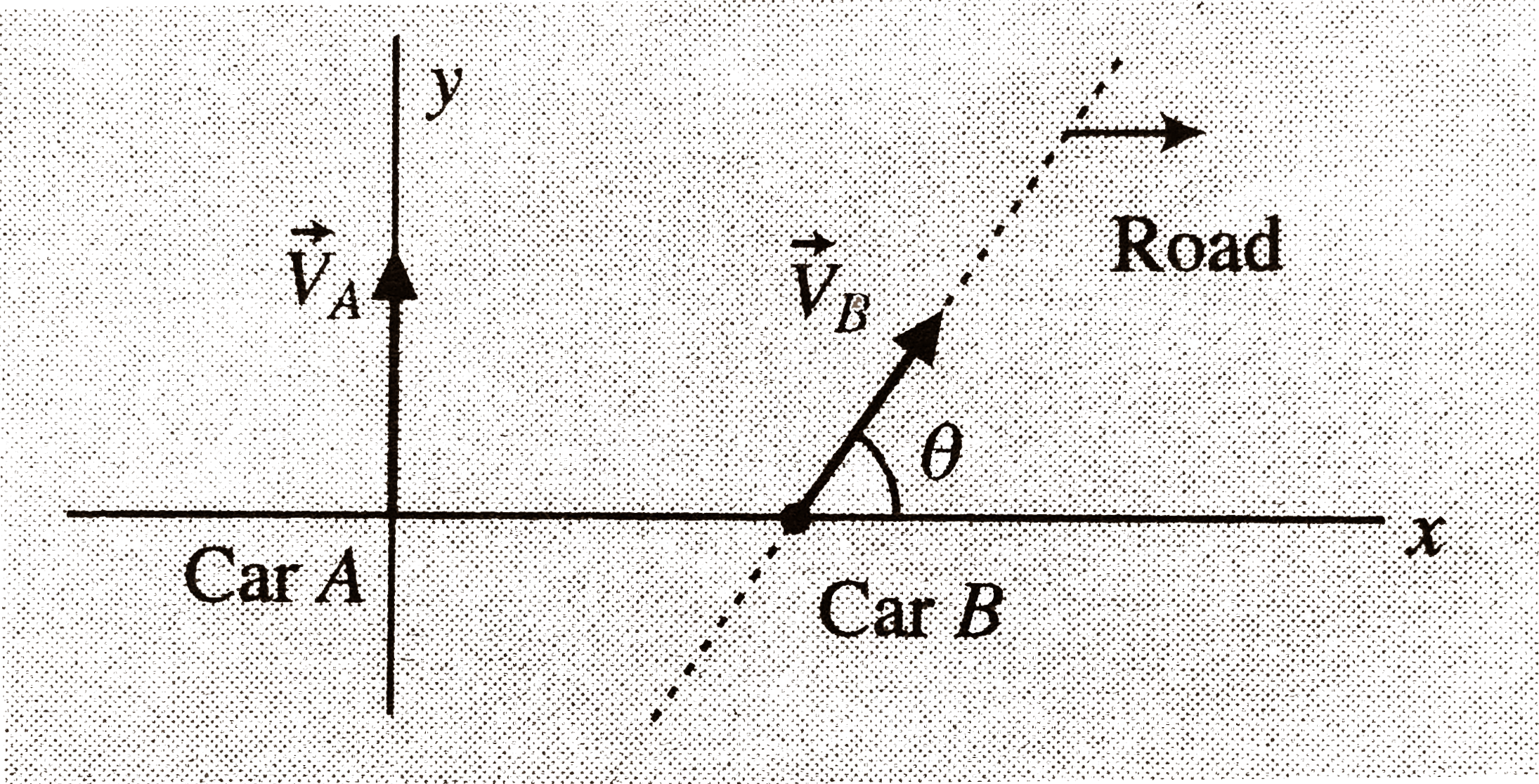 .View Solution
.View SolutionQuestion 37
A man A is sitting in a car at rest observes a man B on bike moving away from him with velocity 16ms−1, a man C walking on road with velocity 2ms−1 towards him and a bird flying with spedd 20ms−1 at angle 37∘ with horizontal as shown in (Fig. 5.74). Find the
(a) velocity of car, bird, and man C as seen by man B.
(b) velocity of car, bird, man B as seen by man C
( c) velocity of car, man B, and man C as seen by bird.
 .View Solution
.View SolutionQuestion 38
Ram Shyam are walking on two perpendicular tracks with speed 3ms−1 and 4ms−1, respectively. At a certain moment (sayt=0s), Ram and Shyam are at 20 m and 40 m away from the intersection of tracks, respectively, and moving towards the intersection of the tracks.
During the motion the magnitude of velocity of ram with respect to Shyam is View SolutionQuestion 41
A political party has to start its procession in an area where wind is blowing at a speed of 30√2kmh−1 and party flags on the cars are fluttering along north - east direction. If the procession starts with a speed of 40kmh−1 towards north, find the direction of flags on the cars.View SolutionQuestion 43
A truck is moving with a constant velocity of 54kmh−1. In which direction (angle with the direction of motion of truck) should a stone be projected up with a velocity of 20ms−1, from the floor of the truck of the truck, so as to appear at right angles to the truck, for a person standing on earth ?View SolutionQuestion 45
A man can swim at the rate of 5kmh−1 in still water. A 1−km wide river flows at the rate of 3kmh−1 The man wishes to swim across the river directly opposite to the starting point.
(a) Along what direction must the man swim ?
(b) What should be his resultant velocity ?
( c) How much time will he take to cross the river ?View SolutionQuestion 46
A river flows due south with a speed of 2.0ms−1. A man strees a motorboat across the river , his velocity relative to the water is 4ms−1 due east. The river is 800m wide.
(a) What is his velocity (magnitude and direction) relative to the earth ?
(b) How much time is required to cross the river ?
( c) HOw far south of his starting points will he reach the opposite bank ?View SolutionQuestion 47
(a) In which direction should the motorboat given in Illustration 5.46 head in order to reach a point on the opposite bank directly east from the starting point ? The boat's speed relative to the water remains 4ms−1.
(b) What is the velocity of the boat relative to the earth ?
( c) How much time is required to cross the river ?View SolutionQuestion 50
A man wants to swim in a river from A→B and back from B→A always following line AB (Fig. 5.94). The distance between points AandB is S. The velocity of the river current v is constant over the entire width of the river. The line AB makes an angle ∝ with the direction of current. The man moves with velocity u at angle β to the line AB. The man swim to cover distance AB and back, find the time taken to complete the journey.
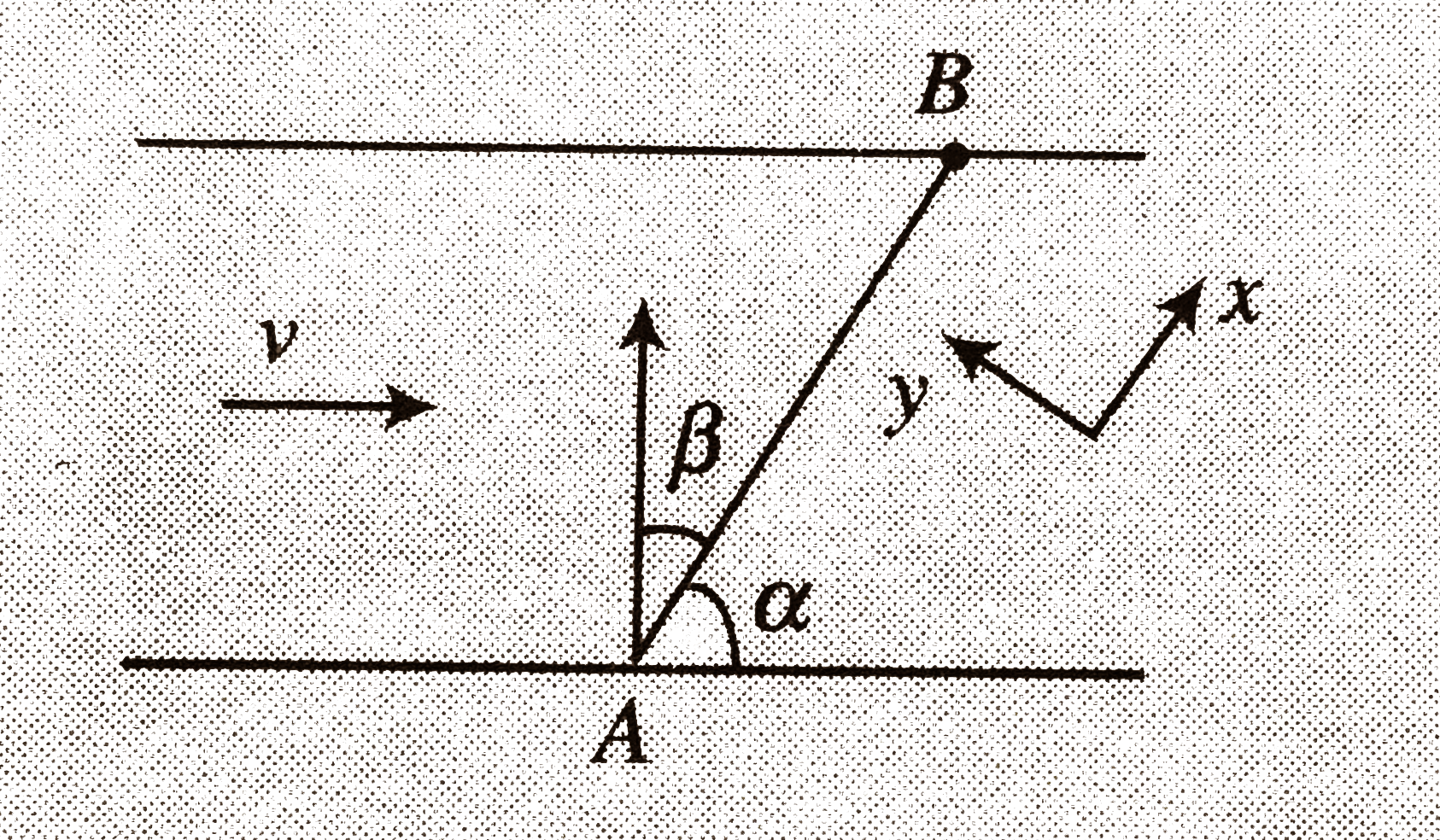 .View Solution
.View SolutionQuestion 53
A standing man observes rain falling with the velocity of 20ms−1 at an angle of 30∘ with the vertical.
(a) Find the velocity with which the amn should move so that rain appears to fall vertically to him.
Now if he futher increases his speed, rain again appears to fall at 30∘ with the vertical. Find his new velocity.View SolutionQuestion 54
A person standing on a road has to hold his umbrella at 600 with the verticcal to keep the rain away. He throws the umbrella an starts running at 20ms−1. He finds that rain drops are hitting his head vertically. Find the speed of the rain drops wigh respect to (a) the road (b) the moving person.View SolutionQuestion 55
A man is coming down an incline of angle 30∘. When he walks with speed 2(√3)ms−1 he has to keep his umbrella vertical to protect himself from rain. The actual speed of rain is 5ms−1. At angle with vertical should he keep his umbrella when he is at rest so that he does not getb drenched ?
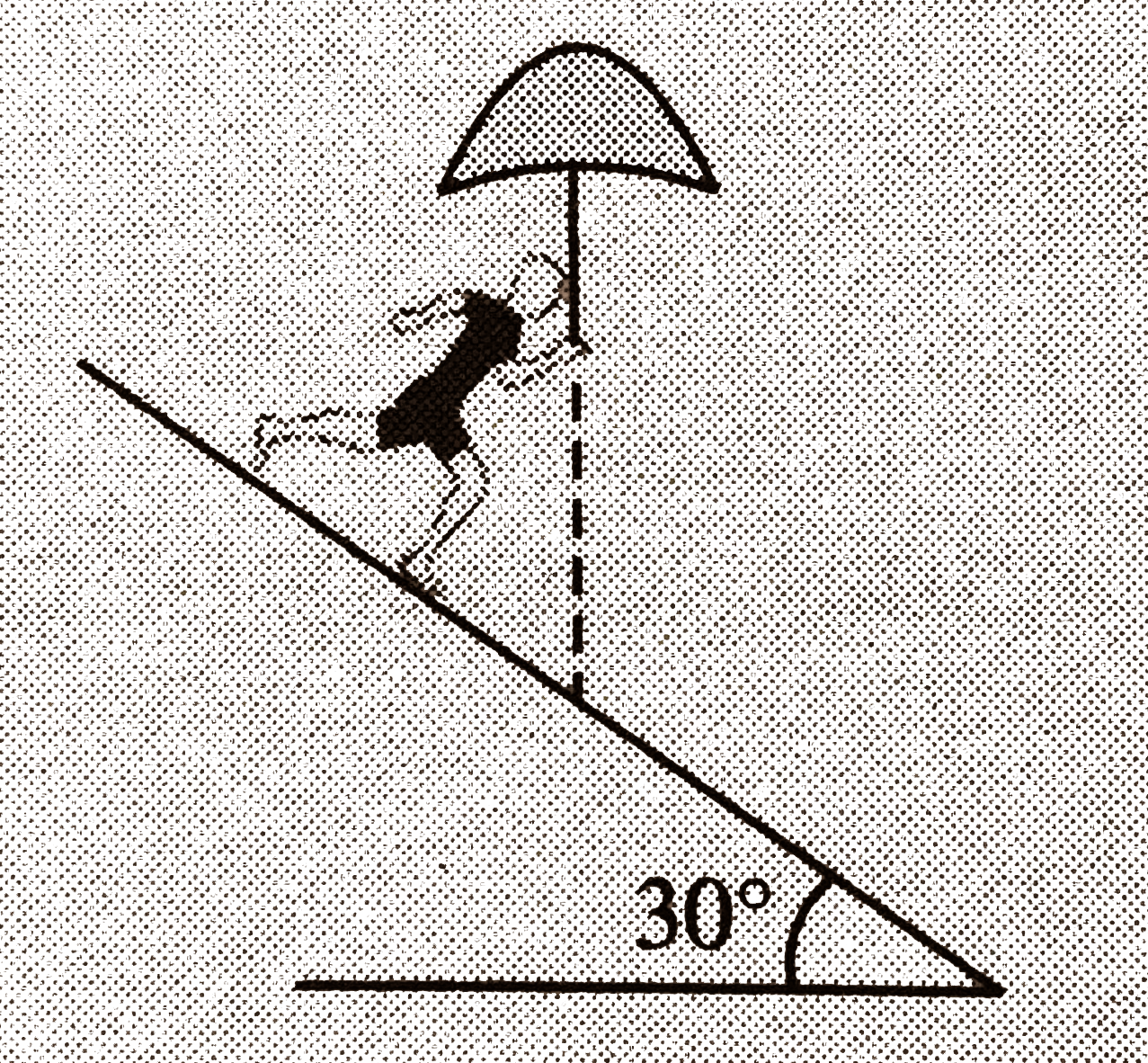 .View Solution
.View SolutionQuestion 56
During a rainy day, rain is falling vertically with a velocity 2m/s A boy at rest starts his motion with a constant acceleration of 2m/s2 along a straight road . Find the rate at which the angle of the axis of umbrella with vertical should be changed so that the rain always falls parallel to the axis of the umbrella.View SolutionQuestion 57
An aeroplane pilot wishes to fly due west A wind of 100kmh−1 is blowing towards south.
(a) If the speed of the plane (its speed in still air) is 300kmh−1 in which direction should the pilot head ?
(b) What is the speed of the plane with respect tom ground ? Illustrate with a vector diagram.View SolutionQuestion 58
A helicopter files horizontally with constant velocity in a direction θ east of north between two points AandB, at distance d apart. Wind is blowing from south with constant speed u, the speed of helicopter relative to air is nu where n>1. find the speed of the helicopter along AB. The helicopter returns from B to A with same speed nu relative to air in same wind. Find the total time for the journeys.
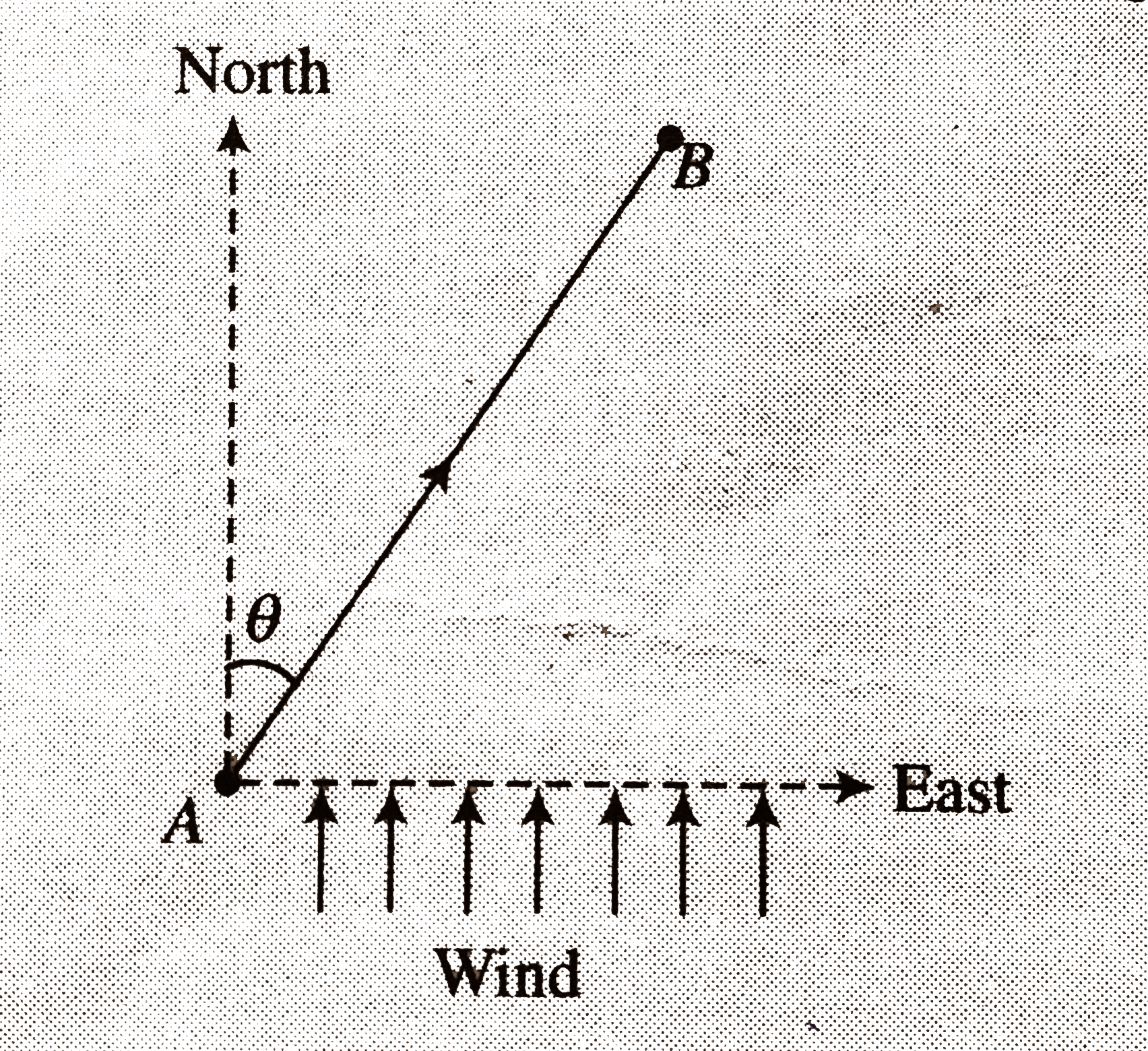 .View Solution
.View SolutionQuestion 59
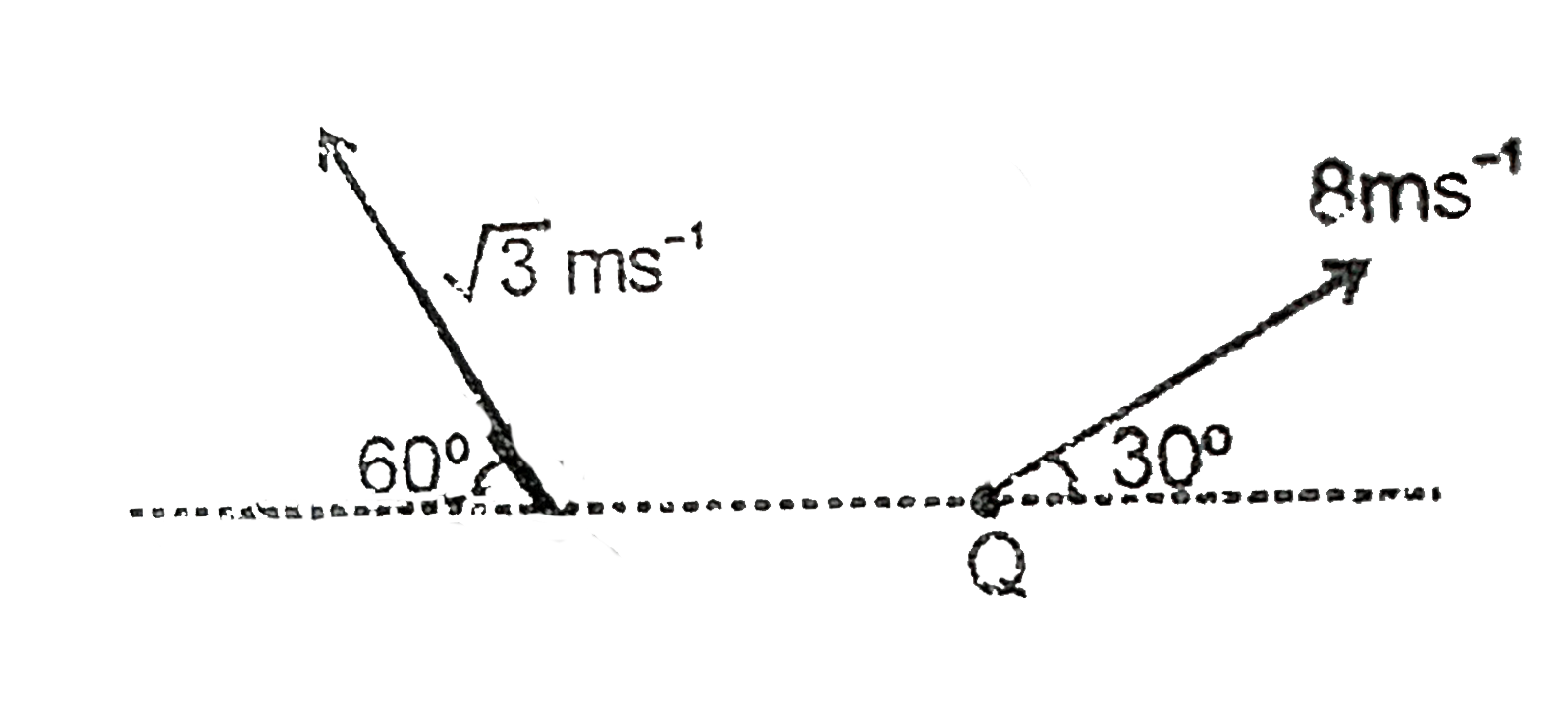
A,B,C,andD are four trees, located at the vertices of a square (Fig. 5.117). Wind blows from A→B with uniform speed. The ratio of times of flight of a bird from A→B and from B→A is n. At what angle should the bird fly from the direction of wind flow, in order that it starts from A and
(a) reaches C,
(b) reaches D ?
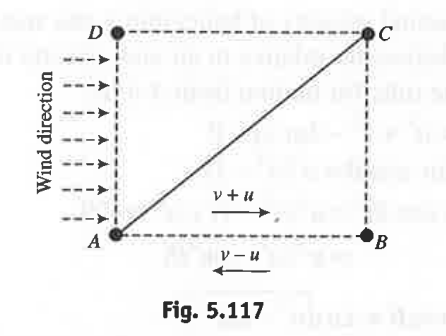 View Solution
View SolutionQuestion 60
Two particles are located on a horizontal plane at a distance 60m. At t=0 both the particles are simultaneously projected at angle 45∘ with velocities 2ms−1and14ms−1, respectively. Find
(a) Minimum separation between them during motion.
(b) At what time is the separation between them minimum ?
 .View Solution
.View SolutionQuestion 62
Two particles AandB are moving with constant velocities v1andv2. At t=0, v1 makes an angle θ0 with the line joining AandBandv2 makes an angle θ2 with the line joining AandB.
(a) Find the condition for AandB to collide.
(b) Find the time after which AandB will collide if separation between them is datt=0.
 .View Solution
.View SolutionQuestion 63
Two cars AandB are moving west to east and south to north, respectively, along crossroads. A moves with a speed of 20ms−1 and is 500m away from the point of intersection of cross roads and B moves with a speed of 15ms−1 and is 400m away from the point of intersection of cross roads. Find the shortest distance between them.View SolutionQuestion 68
A particle moves on a circle of radius r with centripetal acceleration as function of time as ac=k2rt2, where k is a positive constant. Find the following quantities as function of time at an instant :
(a) The speed of the particle
(b) The tangential acceleration of the particle
( c) The resultant acceleration, and
(d) Angle made by the resultant with tangential direction.View SolutionQuestion 71
A fan is rotating with angular velocity 100revs−1. Then is switched off. It takes 5minto stop.
(a) Find the total number of revolution made before the fan stops. (assume uniform angular retardation).
(b) Find the value of angular retardation.
( c) Find the average angular velocity during this interval.View SolutionQuestion 72
Two particles AandB move on a circle Initially, particles AandB are diagonally opposite to each other. Particle A moves with angular velocity πrads−1 and angular acceleration π/2rads−2 and particle B moves with constant angular velocity 2πrads−2. Find the time after which both the particlsd AnadB will collide.View SolutionQuestion 77
Two towers AB and CD are situated at a distance d apart, as shown in figure. AB is 20 m high and CD is 30 m high from the ground. An object of mass m is thrown from the top of AB horizontally with a velocity of 10 m/s towards CD. Simultaneously another object of mass 2 m is thrown fromt the top of CD at an angle of 60∘ to the horizontal towards AB with the same magnitude of initial velocity as that oft he first object. The two objects move in the same vertical plane, collide in mid air and stick to each other (i) calculate the distance between the towers and (ii) find the position where the objects hit the ground.
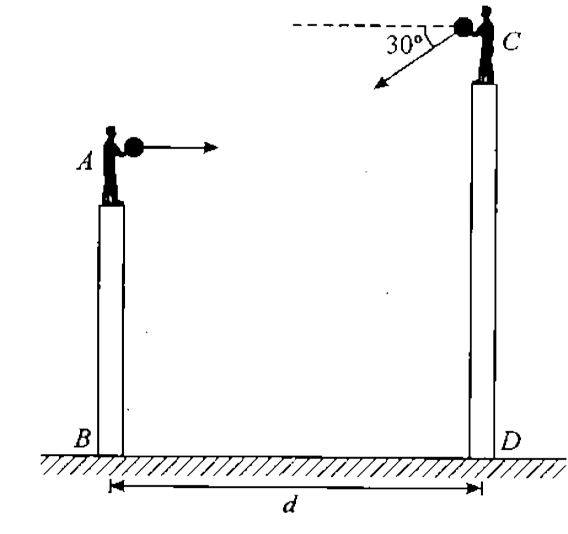 View Solution
View SolutionQuestion 78
Two guns situated at the top of a hill of height 10m fire one shot each with the same speed 5√3m/s at some interval of time. One gun fires horizontal and the other fores upwards at an angle of 60∘ with the horizontal. Two shots collide in air at a poit P. Find (i) time-interval between the firing and (ii) coordinates of the point P. Take the origin of coordinates system at the foot of the hill right below the muzzle and trajectorise in the x−y plane.View SolutionQuestion 79
A large , heavy box is sliding without friction down a smooth plane of inclination θ . From a point P on the bottom of the box , a particle is projected inside the box . The initial speed of the particle with respect to the box is u , and the direction of projection makes an angle α with the bottom as shown in Figure .
(a) Find the distance along the bottom of the box between the point of projection p and the point Q where the particle lands . ( Assume that the particle does not hit any other surface of the box . Neglect air resistance .)
(b) If the horizontal displacement of the particle as seen by an observer on the ground is zero , find the speed of the box with respect to the ground at the instant when particle was projected .
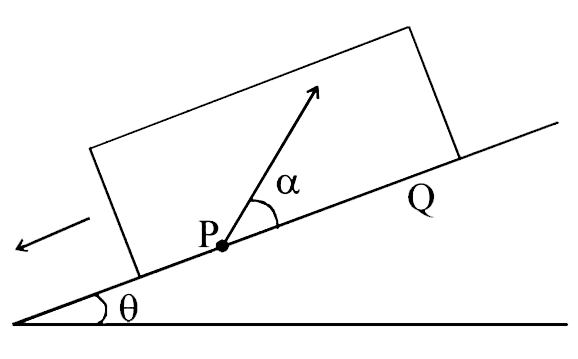 View Solution
View SolutionQuestion 80
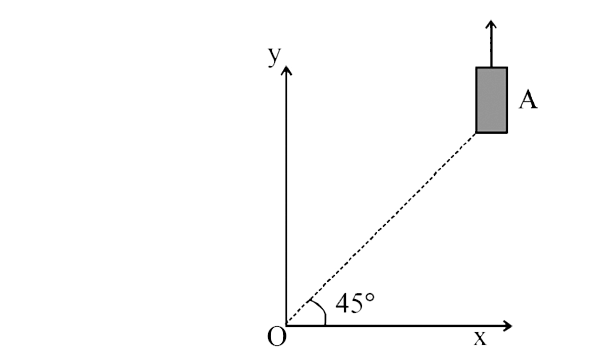
On a frictionless horizontal surface , assumed to be the x−y plane , a small trolley A is moving along a straight line parallel to the y−aξs( see figure) with a constant velocity of (√3−1)m/s . At a particular instant , when the line OA makes an angle of 45(∘) with the x−aξs , a ball is thrown along the surface from the origin O. Its velocity makes an angle ϕ with the x -axis and it hits the trolley .
(a) The motion of the ball is observed from the frame of the trolley . Calculate the angle thetamadebythevelocity→−−→roftheballwiththe x-axis in this frame .
(b) Find the speed of the ball with respect to the surface , if ϕ=(4θ)/(4).
 View Solution
View SolutionQuestion 81
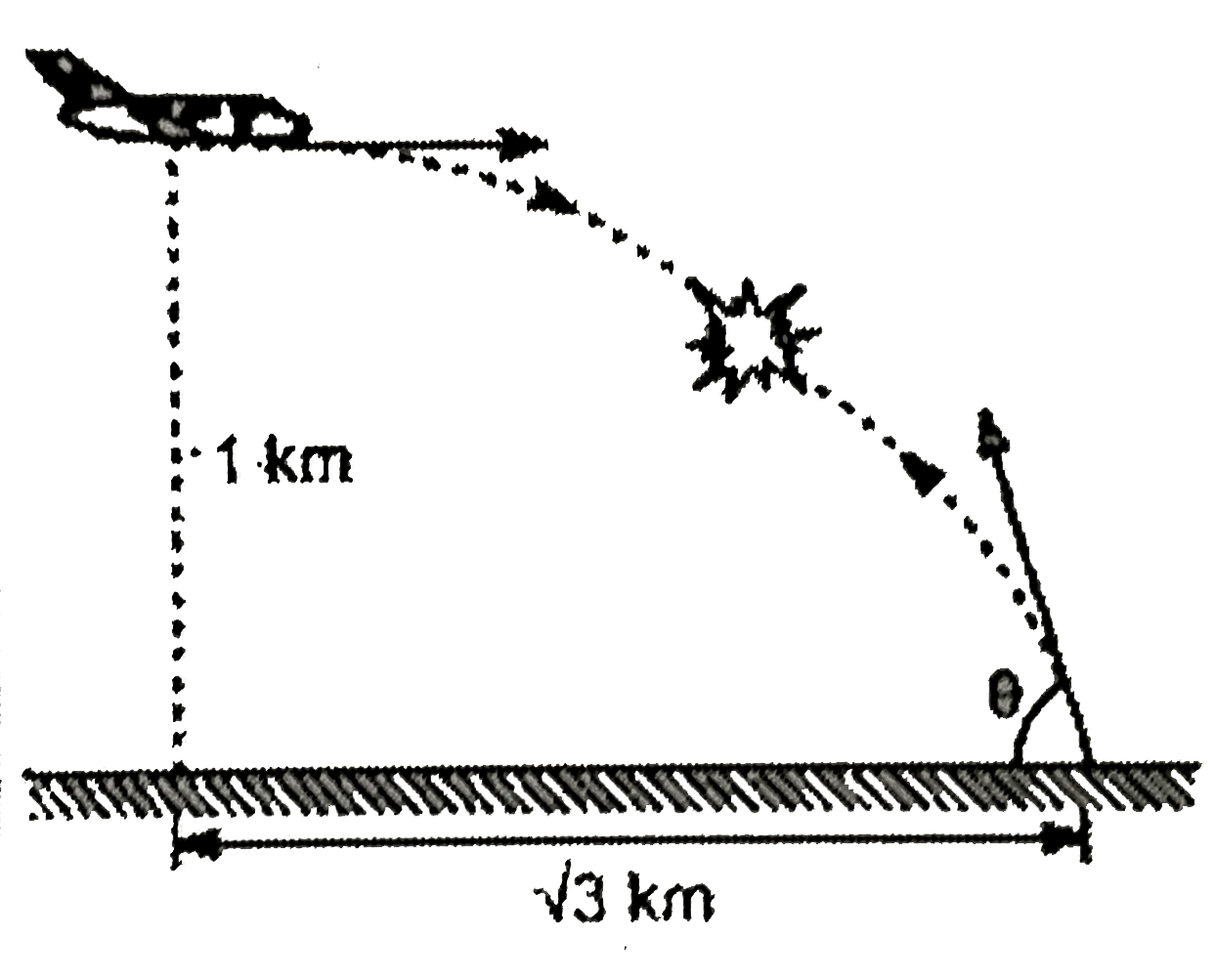
An aircraft is .flying. horizontally with a constant vefocity =200m/s at a height =1km above groun At the momement shown, a bomb is released from the aircraft and the cannon-gun below fires a shell with initial speed =200m/s , at some angle θ For what value of θ will the projectile shell destroy the bomb in mid-air? If the value of θ is 533 , find the minimum distance between the bomb and the shell as they fly past each other. Take sin53∘=4/5
 View Solution
View SolutionQuestion 82
The current velocity of river grows in proportion to the distance from its bank and reaches the maximum value v0 in the middle. Near the banks the velocity is zero. A boat is moving along the river in such a manner that the boatman rows his boat always perpendicular to the current. The speed of the boat in still water is u. Find the distance through which the boat crossing the river will be carried away by the current, if the width of the river is c. Also determine the trajectory of the boat.View Solution
 .
. .
. .
. .
. .
. .
. .
.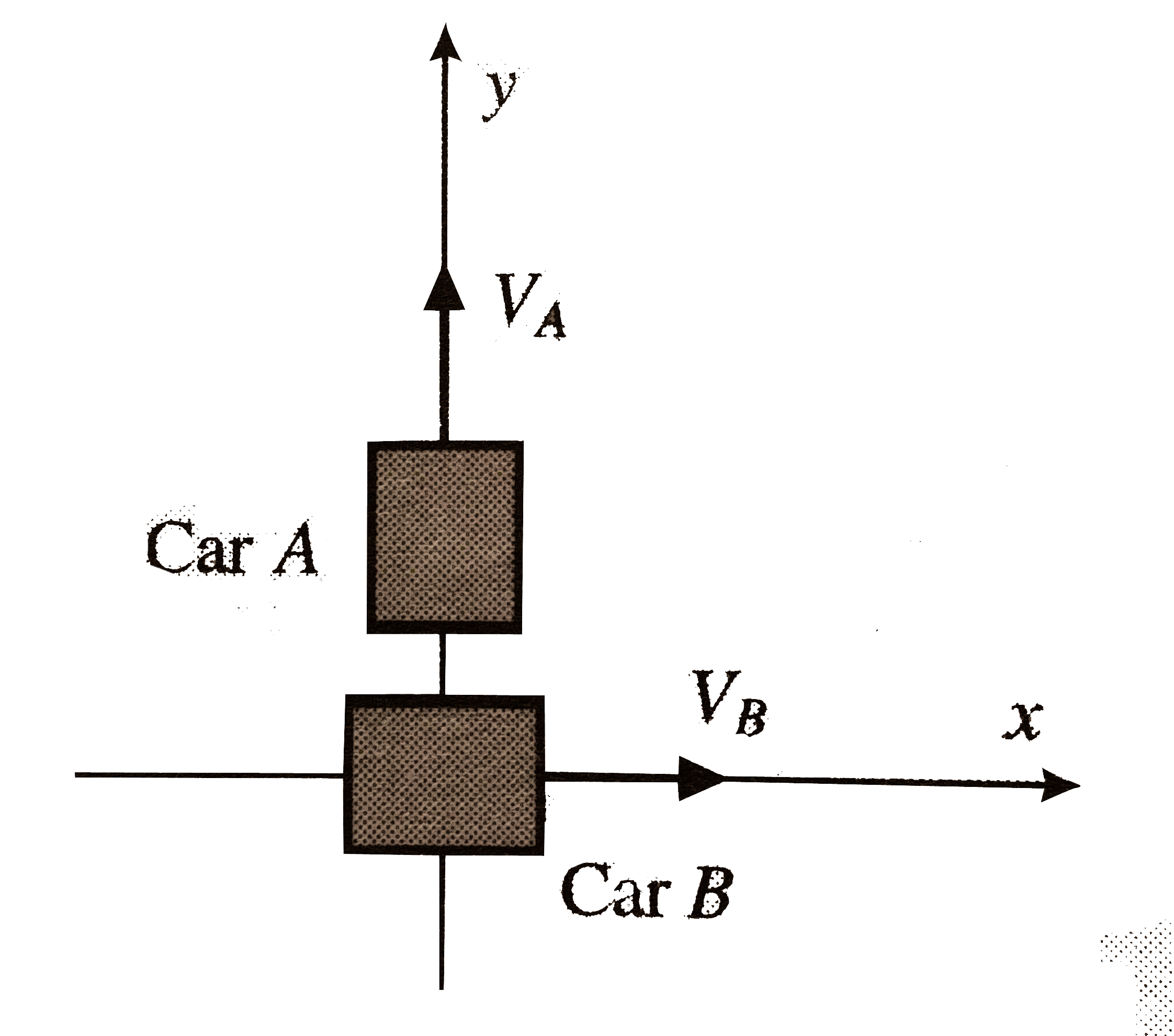 .
.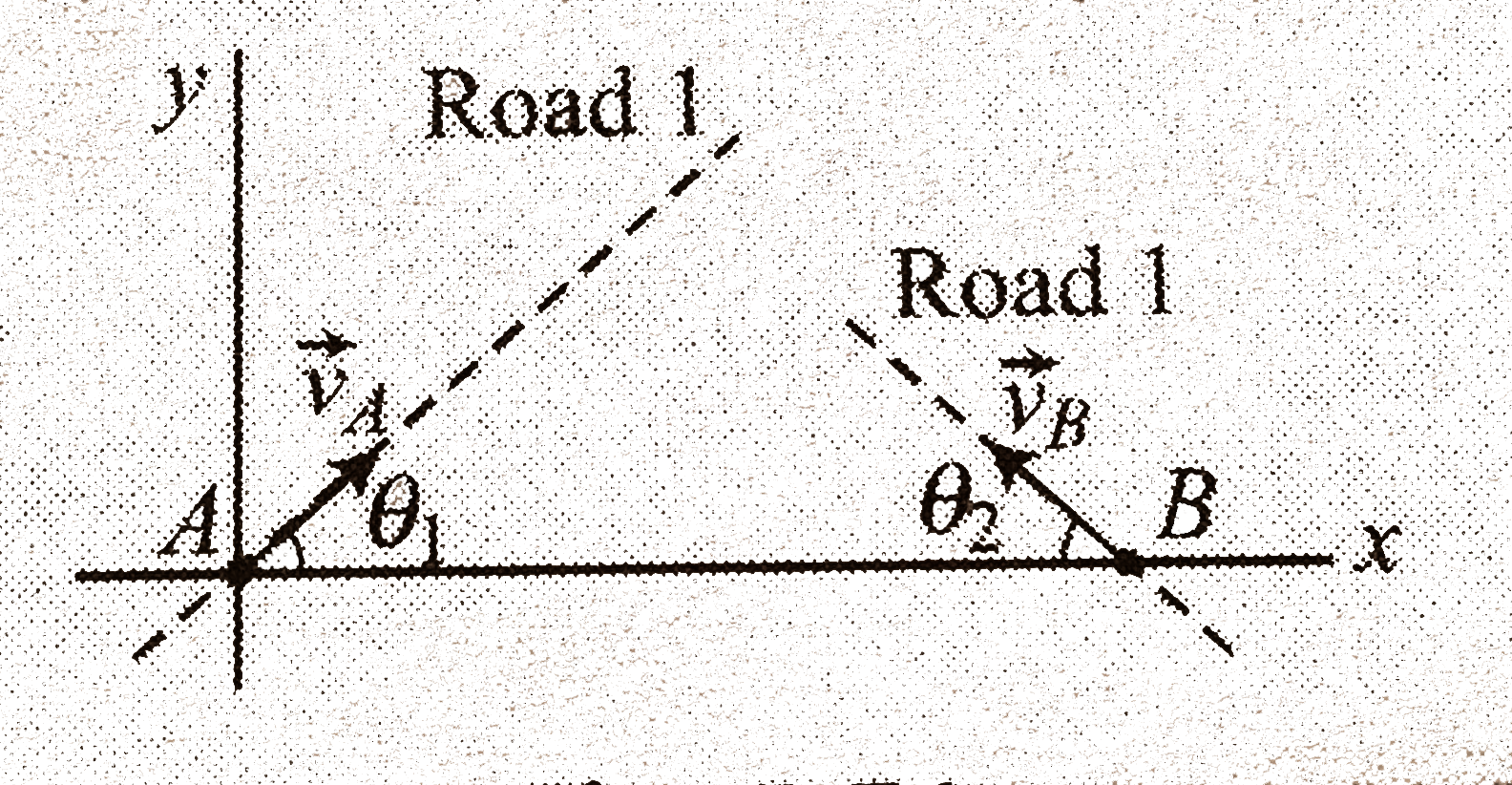 .
. ,
,  .
. .
. .
.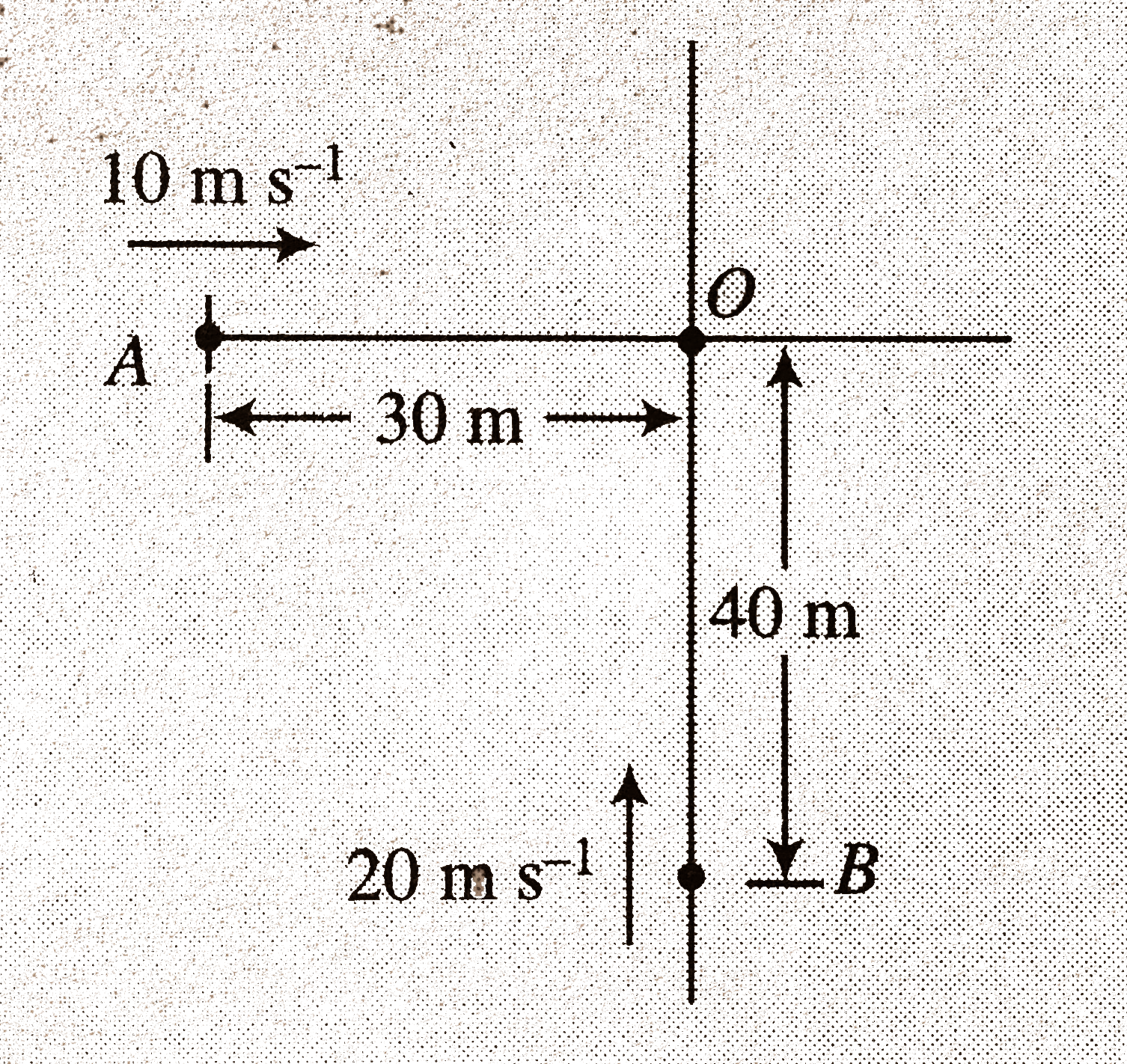 .
. .
.
 .
.