Exercise 5.1 from CENGAGE PHYSICS (HINGLISH) KINEMATICS-2 for Class 11
| Class 11 | PHYSICS |
| Chapter | KINEMATICS-2 |
| CENGAGE PHYSICS (HINGLISH) | Exercise 5.1 |
| Medium | English |
| Academic Year | 2023-2024 |
Question 17
A particle P is projected with velocity u1 at an angle of 30∘ with the horizontal. Another particle Q is thrown vertically upwards with velocity u2 from a point vertically below the highest point of path of P. Determine the necessary condition for the two particles to collide at the highest point.
 .View Solution
.View SolutionQuestion 25
A shell is fired from a gun from the bottom of a hill along its slope. The slope of the hill is ∝=30∘ and the angle of the barrel to the horizontal β=60∘. The initial velocity v of the shell is 21ms−1. Then find the distance of point from the gun at which the shell will fall.View SolutionQuestion 30
A bullet is fired from the bottom of the inclined plane at angle θ=37∘ with the inclined plane. The angle of incline is 30∘ with the horizontal. Find the
(a) position of the maximum height of the bullet from the inclined plane ,
(b) time of light ,
( c) range along the incline ,
(d) the value of θ at which the range will be maximum ,
( e) maximum range.View SolutionQuestion 32
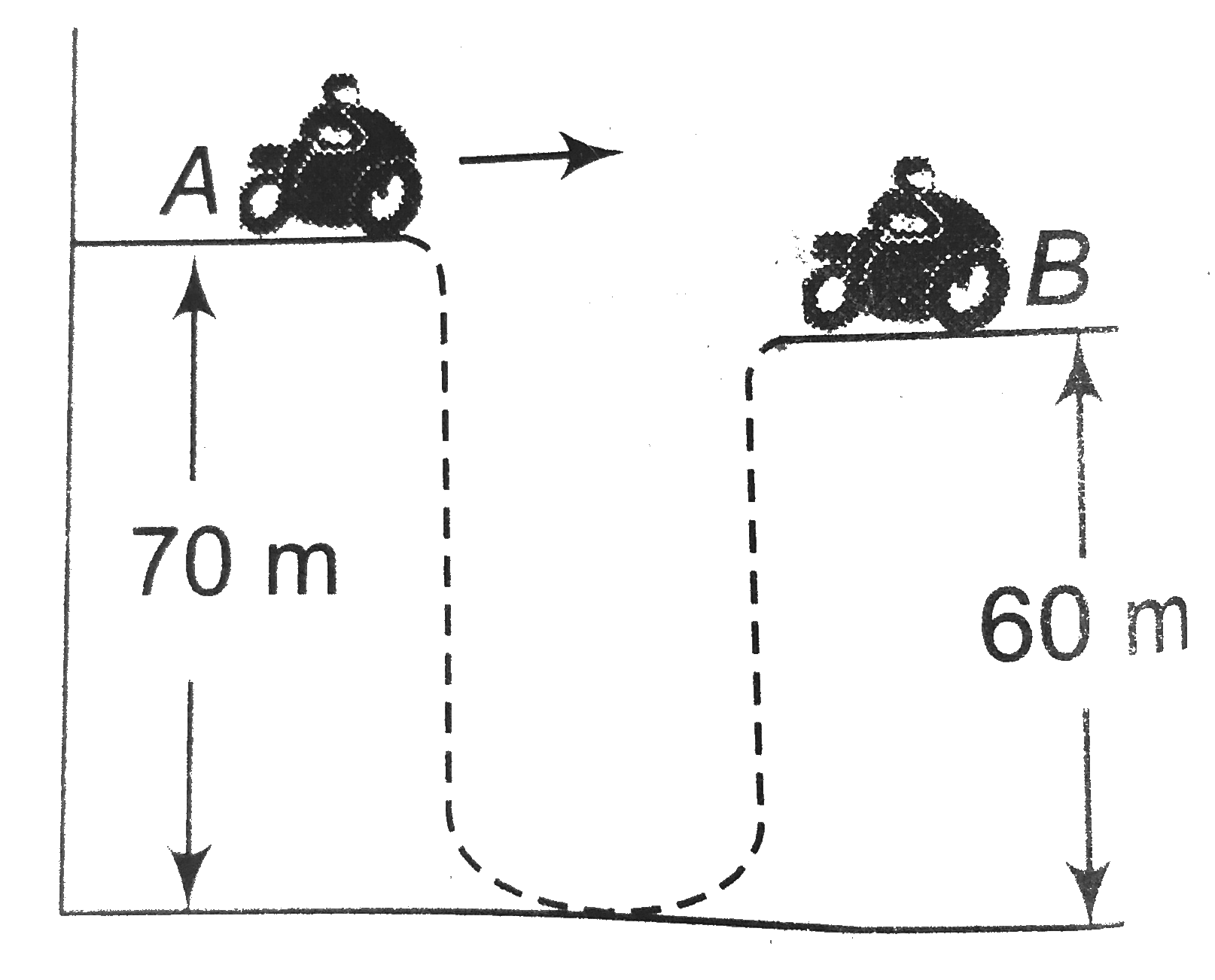
Two stones AandB are projected simultaneously from the top of a 100−m high tower. Stone B is projected horizontally with speed 10ms−1, and stone A is droppd from the tower. Find out the following :
(a) Time of flight of the two stone
(b) Distance between two stones after 3s
(c ) Angle of strike with ground
(d) Horizontal range of particle B.View SolutionQuestion 33
On an inclined plane two particles AandB are projected with same speed at the same angle with the horizontal, particle A down and particle B up the plane. If the ratio of time of flight of AandB is cotθ, where θ is the angle at which B is projected measured from inclined plane, find the angle at which particles are projected.View SolutionQuestion 37
Two guns are situated at the top of a hill firing the shots at the same speed. One gun fires the shot horizontally and other gun fires the shot at an angle of 60∘ with horizontal. Two two shots collide in air. If the time taken by horizontal shot to reach the point of collision in 3seconds, find the time interval between two shots.View SolutionQuestion 41
A 400−m wide river is flowing at a rate of 2.0ms−1. A boat is sailing with a velocity of 10ms−1 with respect to the water, in a direction perpendicular to the river.
(a) Find the time taken by the boat to reach the opposite bank.
(b) How far from the point directly opposite to the starting point does the boat reach the opposite bank ?
( c) In what direction does the boat actually move ?View SolutionQuestion 42
A ,man wishing to cross a river flowing with velocity u jumps at an angle θ with the river flow.
(a) Find the net velocity of the man with respect to ground if he can swim with speed v in still water.
(b) In what direction does the boat actually move ?
( c) Find how far from the point directly opposite to the starting point does the boat reach the opposite bank, if the width of the river is d.View SolutionQuestion 44
To a man running upwards on the hill, the rain appears to fall vertically downwards with 4ms−1. The velocity vector of the man w.r.t. earth is (2ˆi+3ˆj)ms−1. If the man starts running down the hill with the same speed, then determine the relative speed of the rain w.r.t. man.
 .View Solution
.View SolutionQuestion 45
An aeroplane flies along a straight path AandB and returns back again. The distance between AandB is l and the aeroplane maintains the constant speed v w.r.t. wind.
There is a steady wind with a speed u at an angle θ with line AB. Determine the expression for the total time of the trip.
 .View Solution
.View SolutionQuestion 46
A pilot is supposed to fly a certain distance AB, due east from A→B and then due west from B→A. The velocity of plane is v and that of air is u. The time for the round trip is t0 in still air. Show that
(a) if the air velocity be due east or west, the time for round trip will be t1=t0(1−u2v2).
(b) if the air velocity is due north or south, the time for a round trip will be t2=t0√(1−u2v2).
 .View Solution
.View SolutionQuestion 47
Wind blows with a velocity x in the direction shown in (Fig. 5.137). Two aeropalnes starts out from point A and fly with a constant speed y. The first flies from A→B and the other A→C. Both of them return back to A. If AB=AC, then which plane will return to point A first, and what be the ratio of the times of flight of the two planes ?
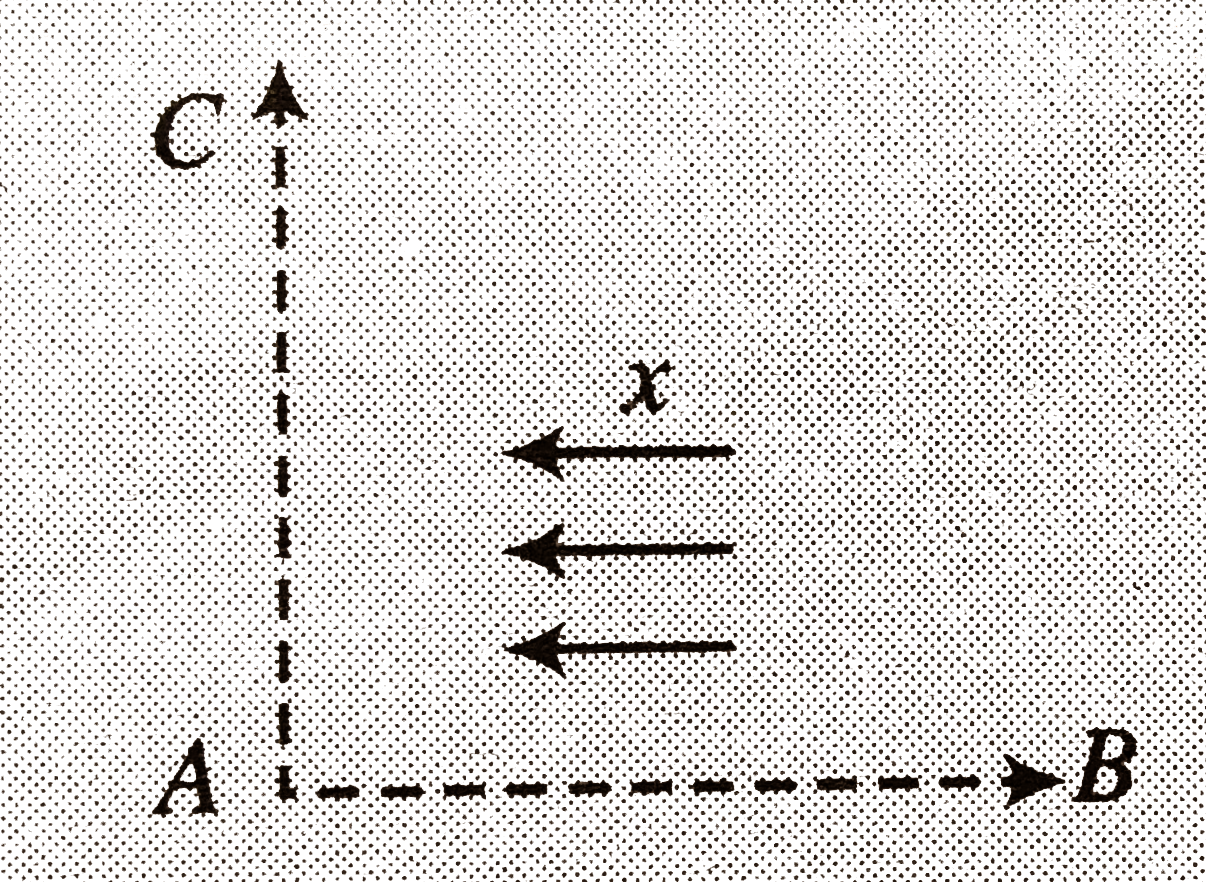 .View Solution
.View SolutionQuestion 63
Two satellities 1and2 orbiting with the time periods T1andT2, respectively, lie on the same line as shown in (Fig. 5.167). After what minimum time, again the satellities will remain on the same line ? Assume that the two satellities should lie in same side of the center of their concentric circular paths.
 .View Solution
.View SolutionQuestion 64
Two particles were projected one by one with the same initial velocity from the same point on level ground. They follow the same parabolic trajectory and are found to be in the same horizontal level, separated by a distance of 1m,2s after the second partice was projected. Assume that the horizontal component of their velocities is 0.5ms−1. Find
(a) the horizontal range of the parabolic path.
(b) the maximum height for the parabolic path.View SolutionQuestion 66
Cannon A is located on a plain a distance L from a wall of height H. On top of this wall is an idential cannon (cannon B). Ignore air resistance throughout this problem.
Also ignore the size of the cannons relative to LandH. The two groups of gunners aim the cannons directly at each other. They fire at each other simultaneously, with equal muzzle speed v0
What is the velue of v0 for which the two cannon balls collide just as they hit the ground ?
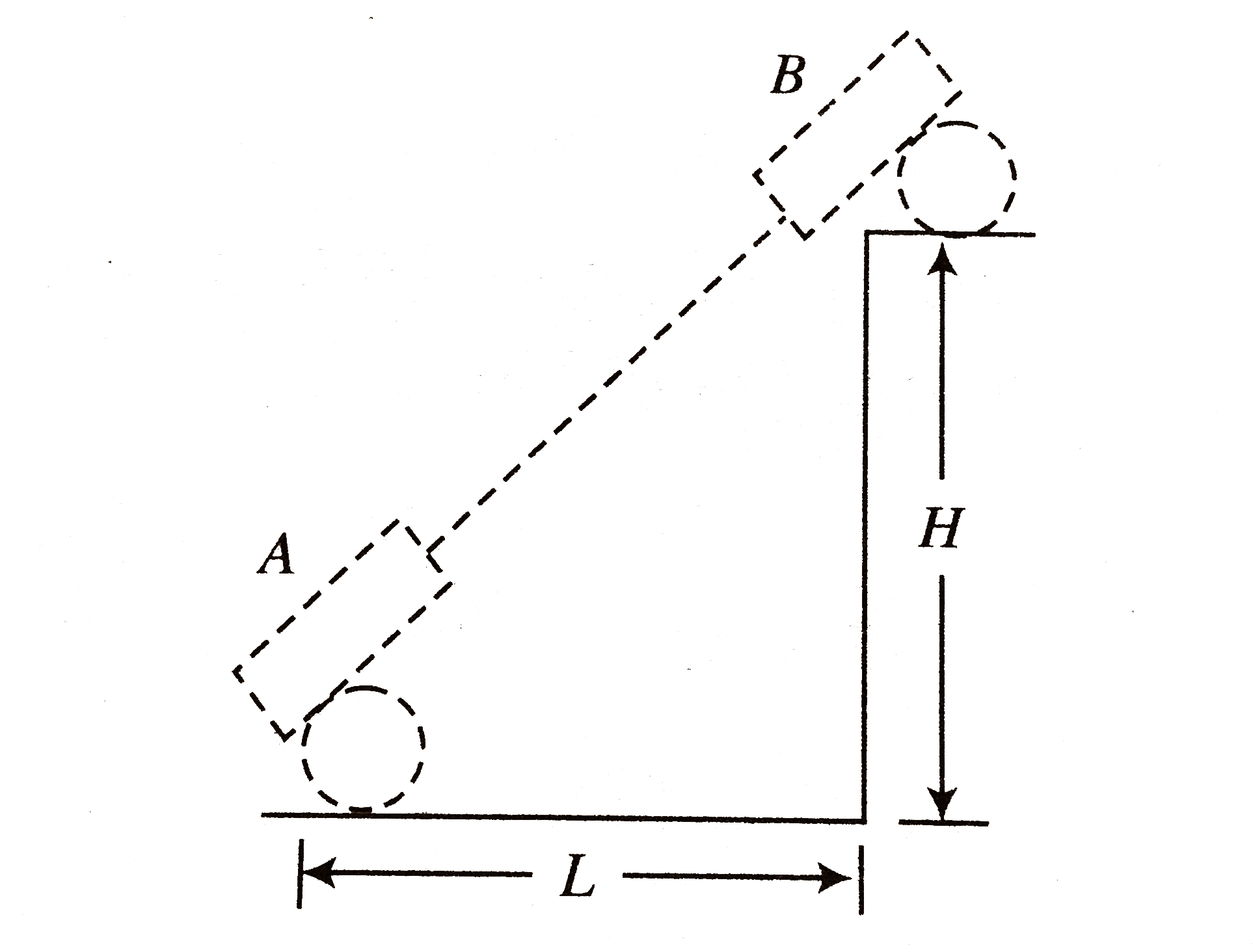 .View Solution
.View SolutionQuestion 67
A platform is moving upwards with a constant acceleration of 2ms−2. At time t=0, a boy standing on the platform throws a ball upwards with a relative speed of 8ms−1. At this instant, platform was at the height of 4m from the ground and was moving with a speed of 2ms−1. Take g=0ms−2. Find
(a) when and where the ball strikes the platform.
(b) the maximum height attained by the ball from the ground.
( c) the maximum distance of the ball from the platform.View SolutionQuestion 68
A stone is projected from the ground in such a direction so as to hit a bird on the top of a telegraph post of height h and attains the maximum height of 2h above the ground. If at the insatant of projection, the bird were to fly away horizontally with a uniform speed, find the ratio between the horizontal velocity of bird and the horizontal component of velocity of stone, if the stone hits the bird while descending. View SolutionQuestion 71
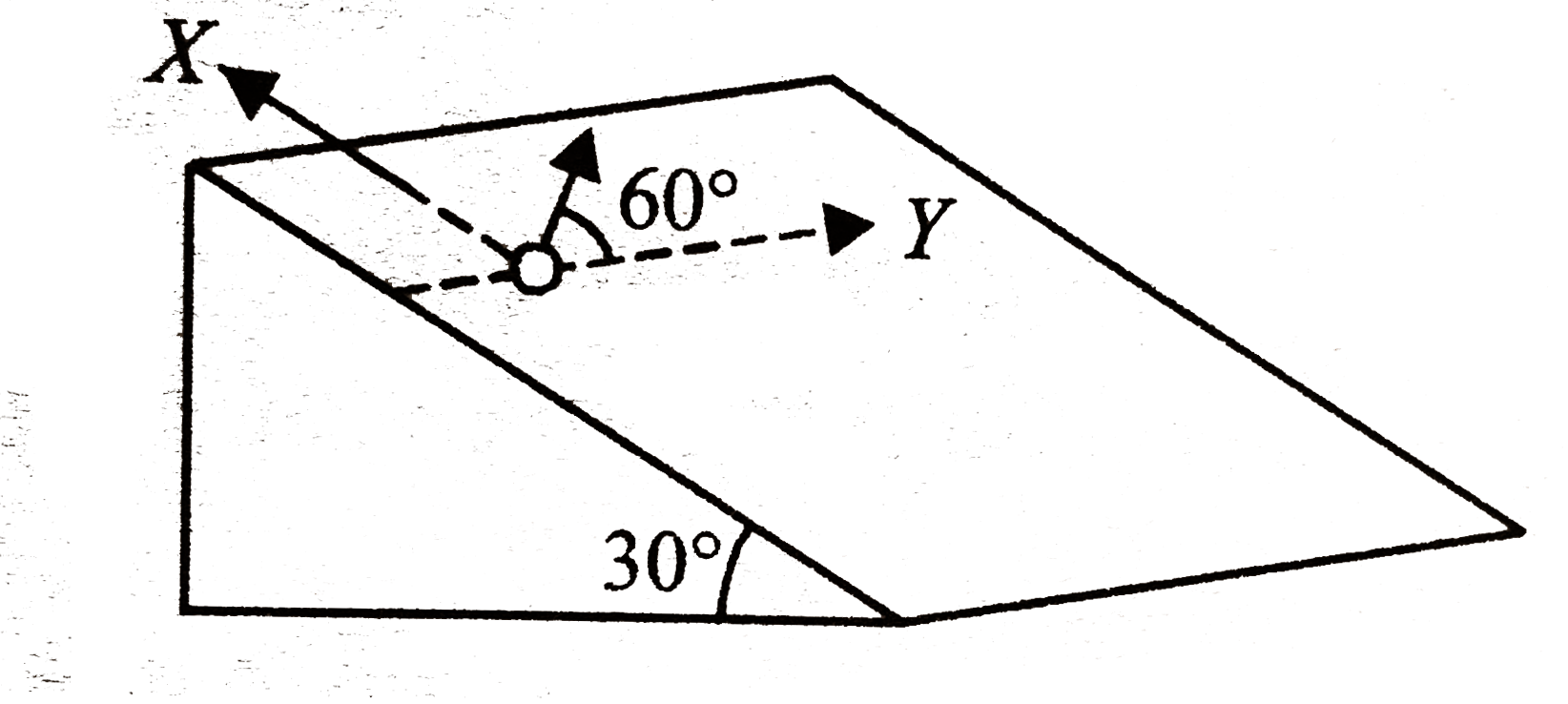
A launch travels across a river from a point A to a point B of the opposite bank along the line AB forming angle ∝ with the bank. The flag on the mast of the launch makes an angle β with its direction of motion. Determine the speed of the launch w.r.t. the bank. The velocity of wind is u perpendicular to the stream.
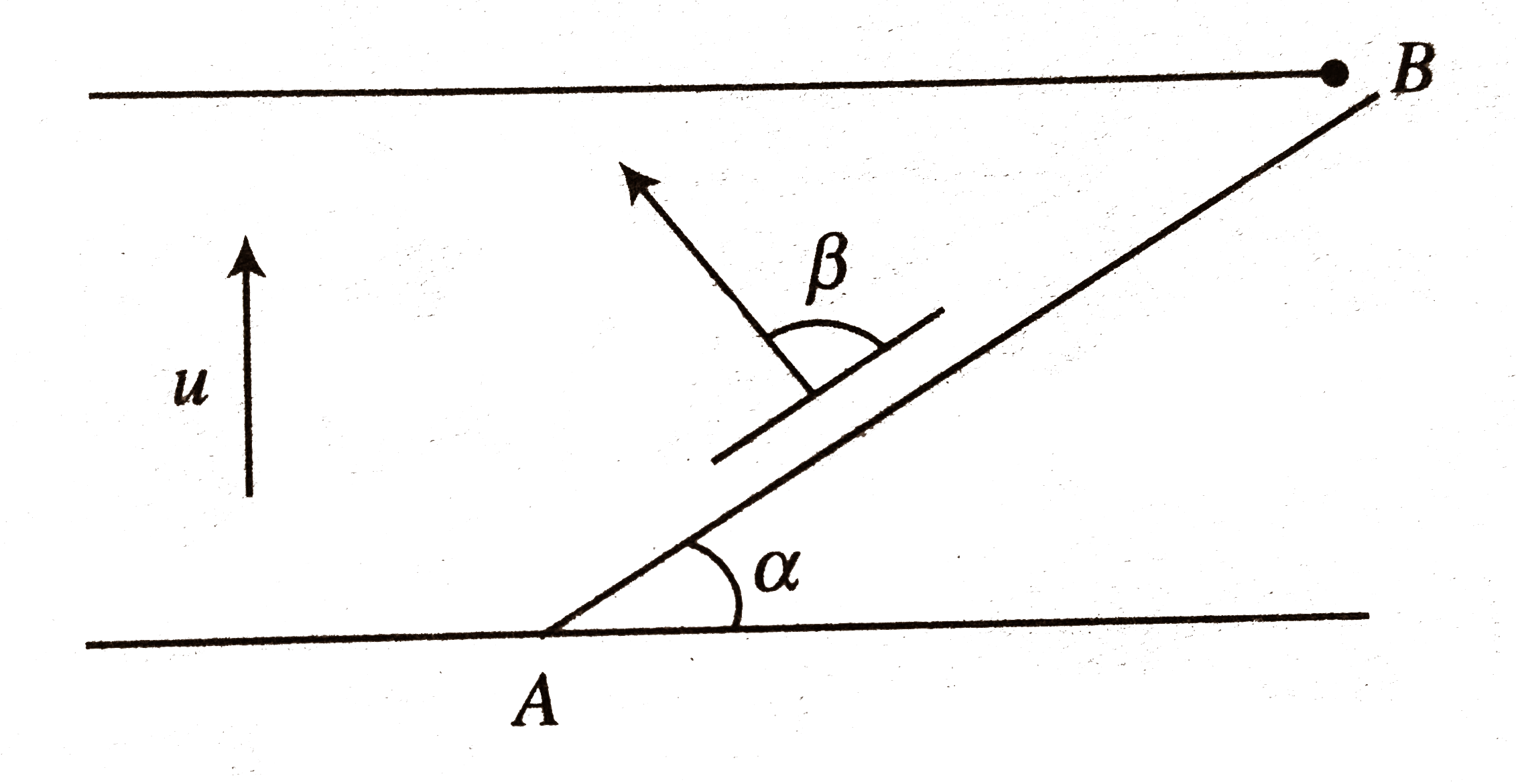 .View Solution
.View SolutionQuestion 72
An airplane is observed by two observers traveling at 60kmh−1 in two vehicles moving in opposite directions on a straight road. To an observer in one vehicle, the plane appears to cross the road track at right angles while to the other appears to be 45∘. At what angle does the plane actually cross the road track and what is its speed relative to ground ?View SolutionQuestion 73
Ball I is thrown towards a tower at an angle of 60∘ with the horizontal with unknown speed (u). At the same moment, ball II is released from the top of tower as shown in (Fig. 5.189). Balls collide after 2s and at the moment of collision, the velocity of ball I is horizontal. Find the
(a) speed u
(b) distance of point of projection of ball I from base of tower (x)
( c) height of tower
 .View Solution
.View SolutionQuestion 74
A ball is fired from point P, with an initial speed of 50ms−1 at an angle of 53∘, with the horizontal. At the same time, a long wall ABat200m from point P starts moving toward P with a constant speed of 10ms−1. Find
(a) the time when the ball collides with wall AB.
(b) the coordinate of point C, where the ball xollides, taking point P as origin.
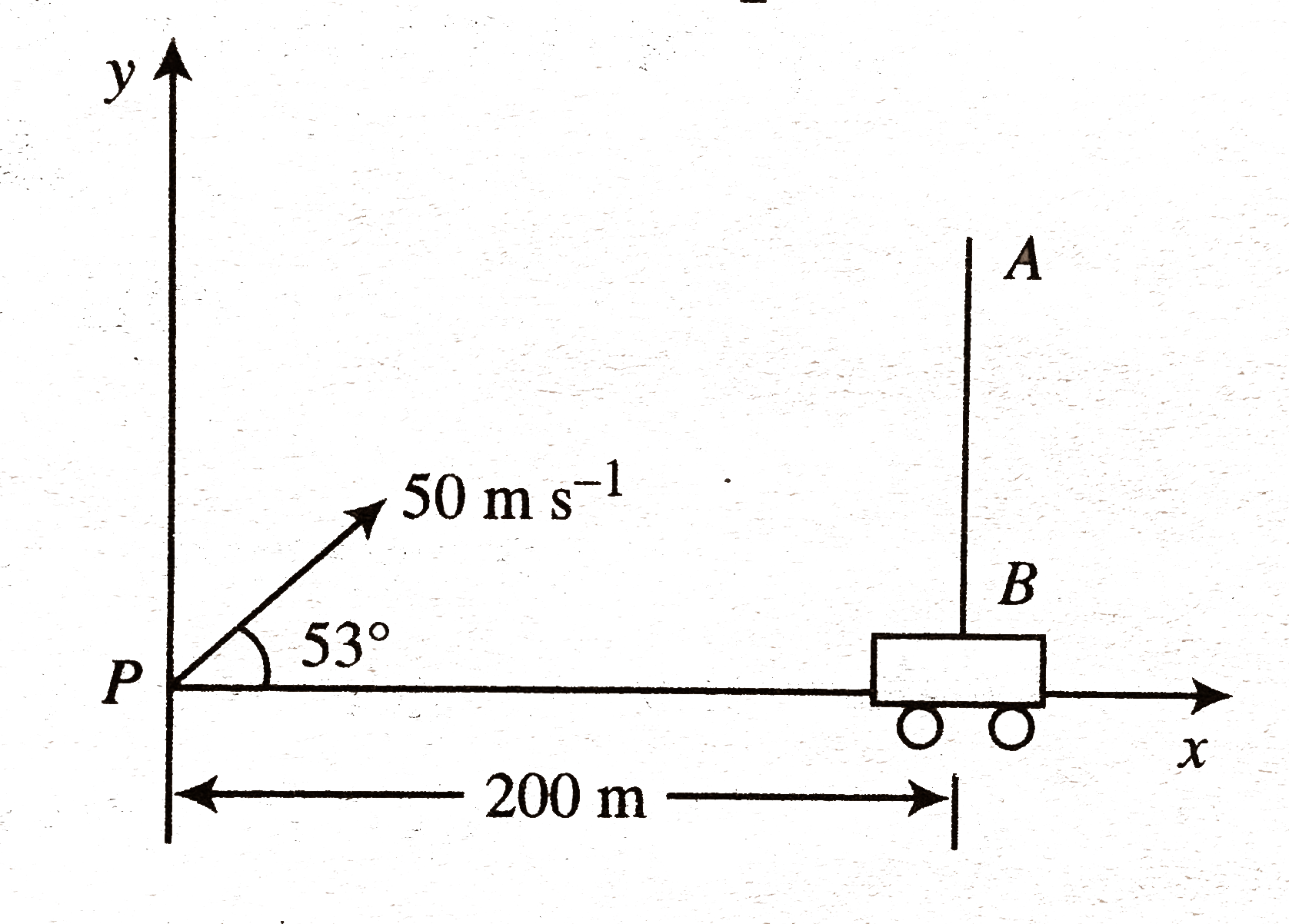 .View Solution
.View SolutionQuestion 76
A boy throws a ball with speed u in a well of depth 14m as shown in (Fig. 5.191). On bounce with the bottom of the well, the speed of the ball gets halved. What should be the minimum value of u(inms−1) such that the ball may be able to reach his hands again ? It is given that his hands are at 1m height from top of the well while throwing and catching.
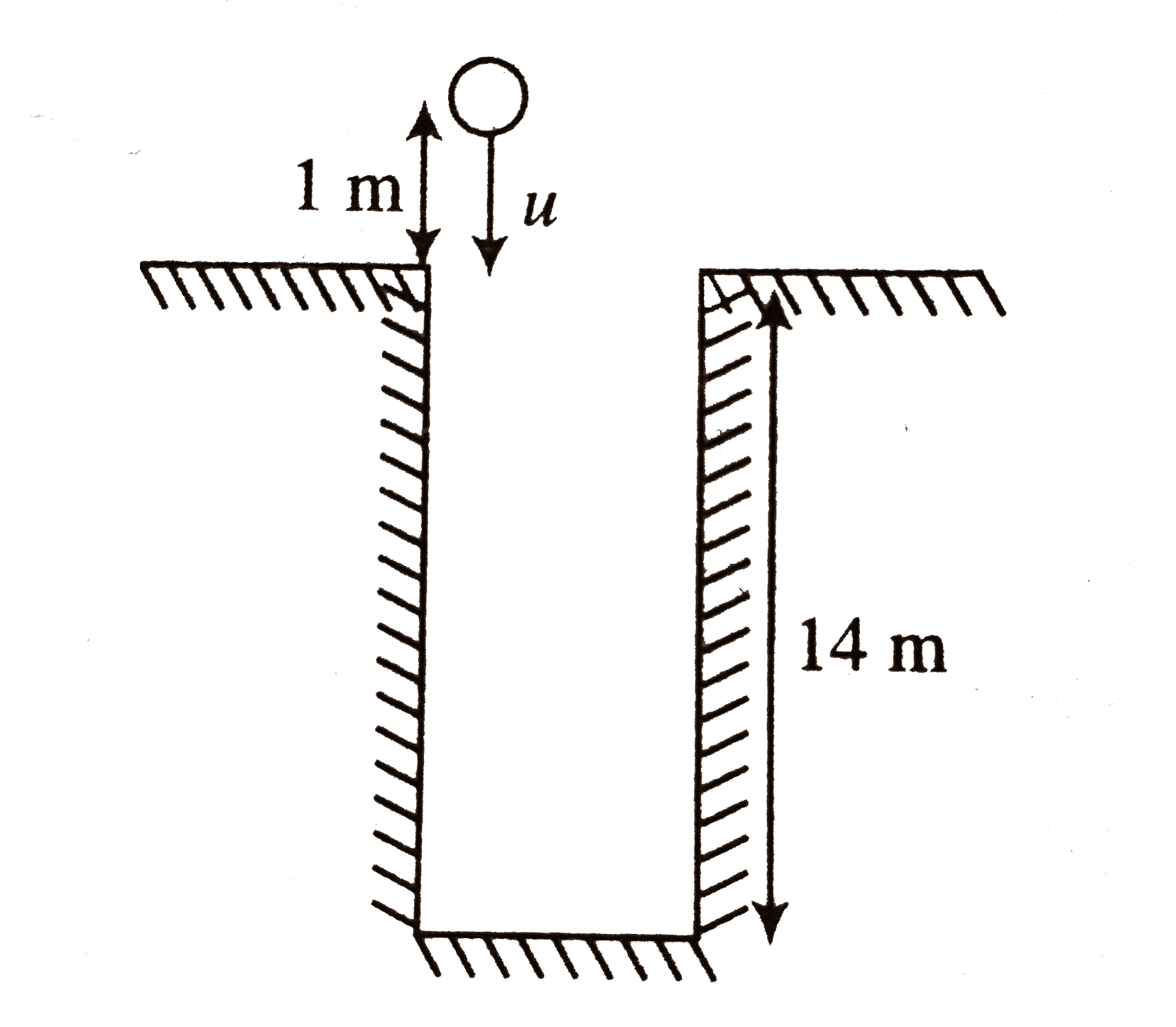 .View Solution
.View SolutionQuestion 77
A helicopter is moving verticallly upwards with a velocity 5ms−1. When the helicopter is at a height 10m from ground, a stone is thrown with a velocity (3ˆi+4ˆj)ms−1 from the helicopter w.r.t. the man in it. Considering the point on ground vertically below the helicopter as the origin of coordinates, and the ground below as xy plane, find the coordinates of the point where the stone will fall, its distance from origin at the instant the stone strikes the ground, assuming helicopter moves upwards with constant velocity.
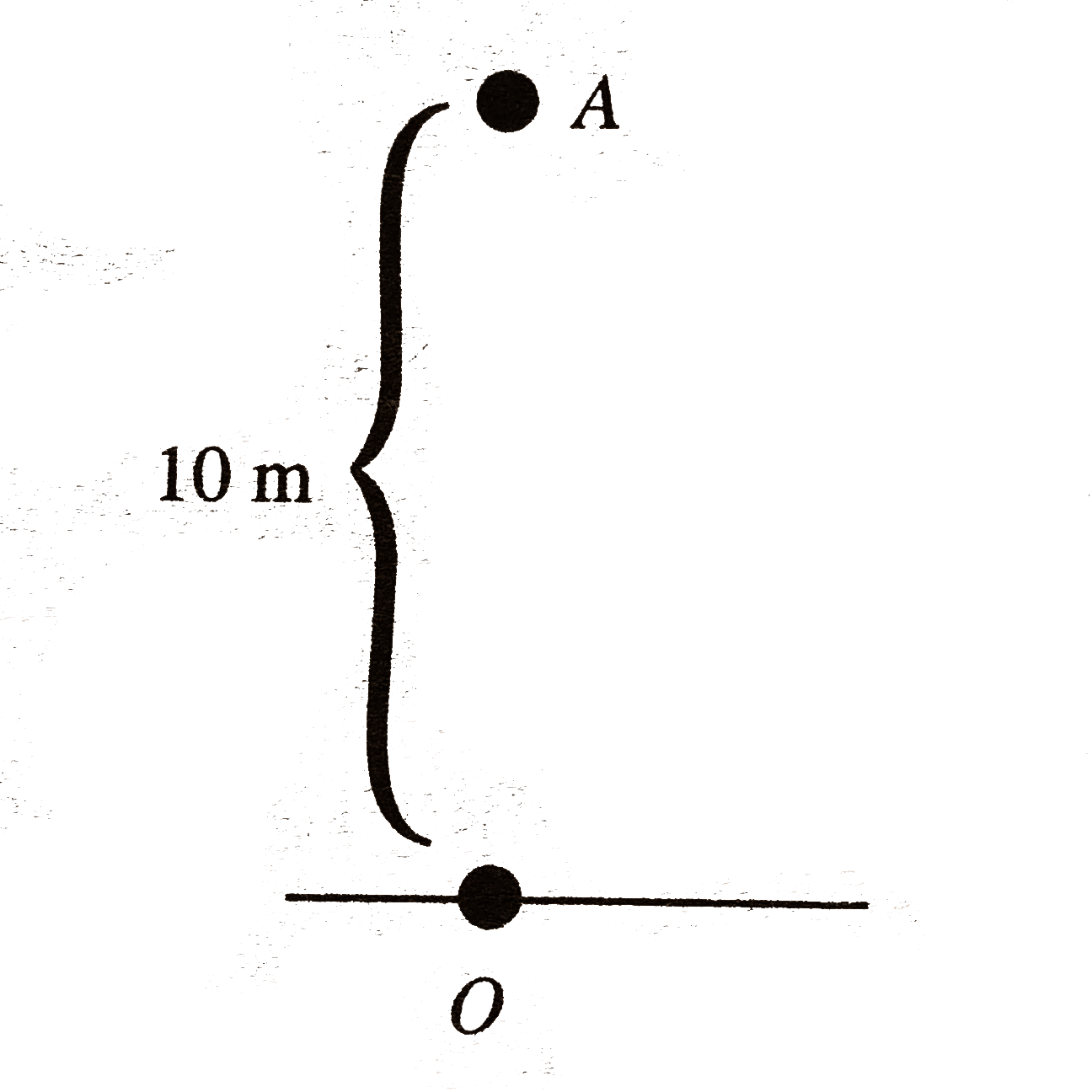 .View Solution
.View SolutionQuestion 79
A boy on a train of height h1 projects a coin his friend of height h2 standing on the same train, with a velocity v relative to the train, at an angle θ with horizontal. If the train moves with a constant velocity v' in the direction of x - motion of the coin, find the
(a) distance between the boys so that the second boy can catch the coin,
(b) maximum height attained by the coin, and
( c) speed with which the second boy catches the coin relative to himself (train) and ground.View SolutionQuestion 82
A bomber plane moves due east at 100kmh−1 over a town T at a certain instant of time. Six minutes later, an interceptor plane sets off flying due north - east from the station S which is 40km south of T. If both maintain their courses, find the velocity with which the interceptor plane must fly in order to just overtake the bomber.View SolutionQuestion 83
The velocity if a swimmer (v) in stil water is less than the velocity of water (u) in a river. Show that the swimmer must aim himself at an angles cos−1 (v/u) with upstream in order to cross the river along the shortest possible path. Find thr drifting (distance moved along the direction of stream in crossing the river) of the swimmer along this shortest possible path.View SolutionQuestion 85
A steamer plies between two stations AandB on opposite banks of a river, always following the path AB. The distance between stations AandB is 1200m. The velocity of the current is √17ms−1 and is constant over the entire width of the river. The line AB makes an angle 60∘ with the direction of the flow. The steamer takes 5min to cover the distance AB and back.
(a) Find the velocity of steamer with respect to water.
(b) In what direction should the steamer move with respect to line AB ?View SolutionQuestion 88
The front wind screen of a car is inclined at an 60∘ with the vertical. Hailstones fall vertically downwards with a speed of 5√3ms−1. Find the speed of the car so that hailstones are bounced back by the screen in vertically upward direction with respect to car. Assume elastic collision of hailstones with wind screen.View SolutionQuestion 89
A particle is projected from point A to hit an apple as shown in (Fig.). The particle is directly aimed at the apple. Show that particle will not hit the apple. Now show that if the string with which the apple is hung is cut at the time of firing the particle, then the particle will hit the apple.
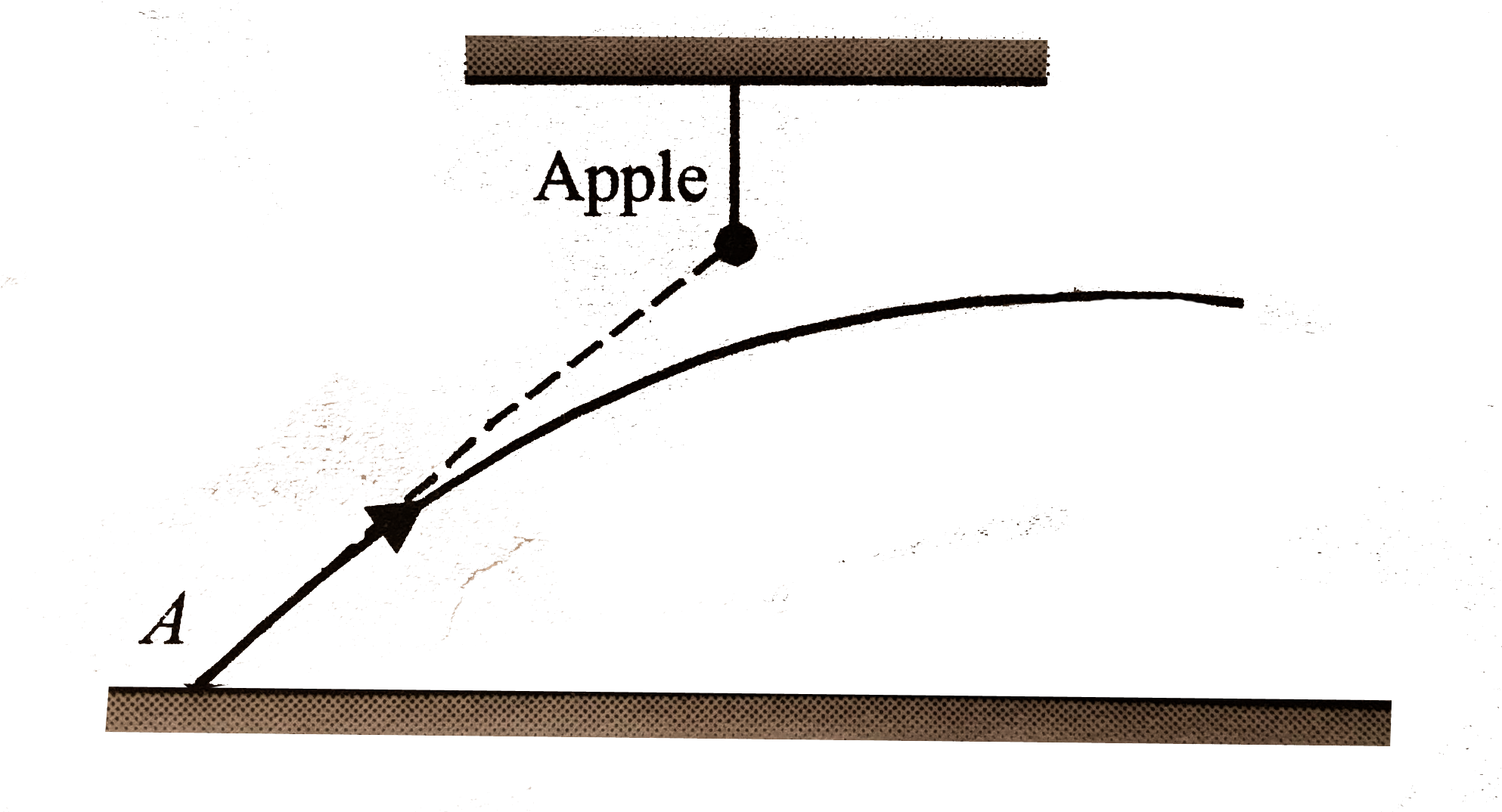 .View Solution
.View SolutionQuestion 92
A stone is projected from the ground in such a direction so as to hit a bird on the top of a telegraph post of height h and attains the maximum height of 2h above the ground. If at the insatant of projection, the bird were to fly away horizontally with a uniform speed, find the ratio between the horizontal velocity of bird and the horizontal component of velocity of stone, if the stone hits the bird while descending. View SolutionQuestion 95
shows an elevator cabin, which is moving downwards with constant acceleration a . A particle is projected from corner A, directly towards diagonally opposite corner C. Then prove that
(a) particle will hit C only when a=g.
(b) Particle will hit the wall CDifa<g.
( c) Particle will hit the roof BCifa>g.
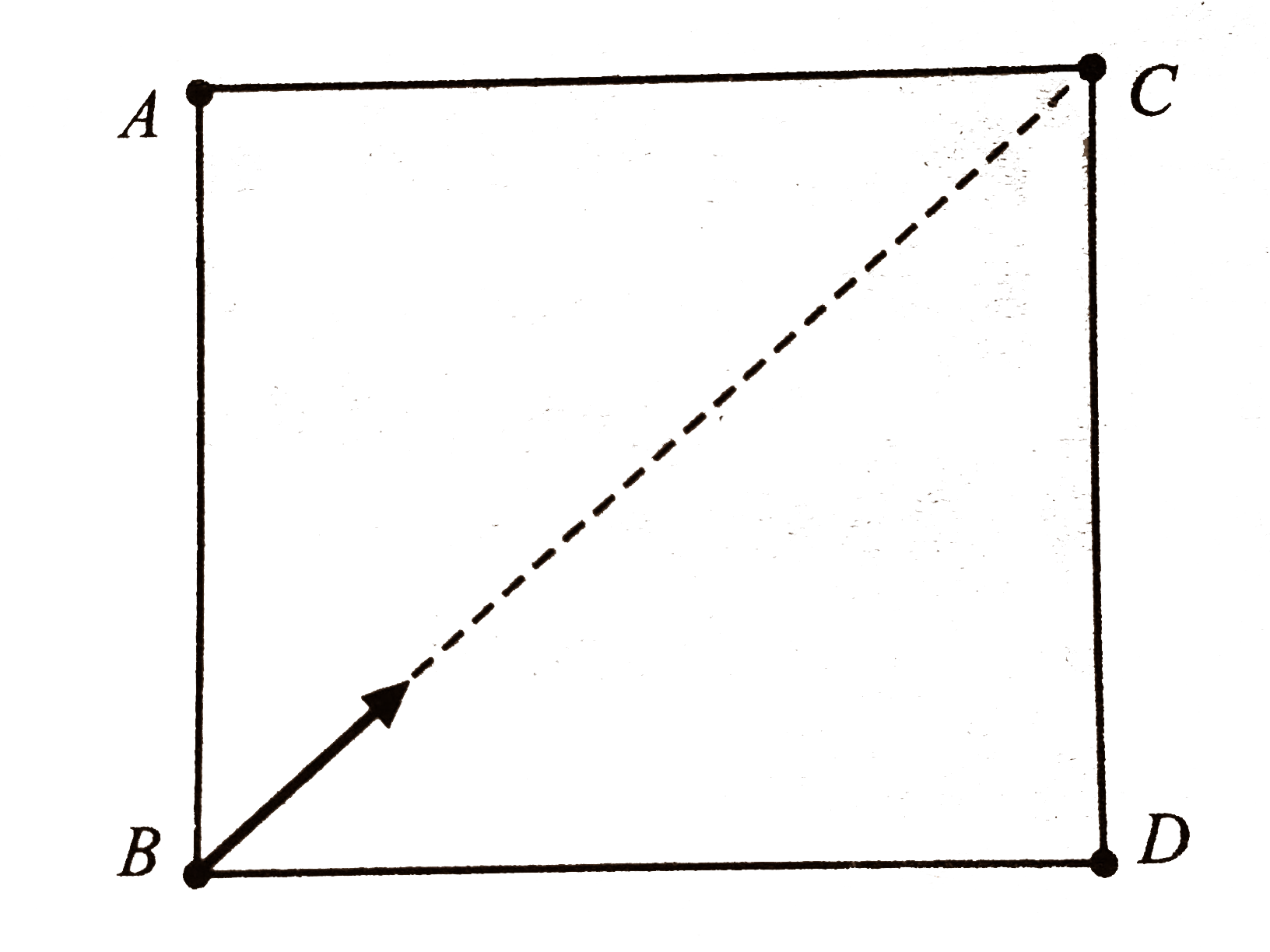 .View Solution
.View SolutionQuestion 98
Two parallel straight lines are inclined to the horizon at an angle ∝. A particle is projected from a point mid way between them so as to graze one of the lines and strikes the other at right angle. Show that if θ is the angle between the direction of projection and either of lines, then tanθ=(√2−1)cot∝.View SolutionQuestion 101
A cylclist is riding with a speed of 27kmh−1. As he approaches a circular turn on the road of radius 80m, he applies brakes and reduces his speed at the constant rate of 0.5ms−2. What is the magnitude and direction of the net acceleration of the cyclist on the circular turn ?View SolutionQuestion 103
A particle starts from rest and moves in a circular motion with constant angular acceleration of 2rads−2. Find
(a) Angular velocity
(b) Angular displacement of the particle after 4s.
( c) The number of revolutions completed by the particle during these 4s.
(d) If the radius of the circle is 10cm, find the magnitude and direction of net acceleration of the particle at the end of 4s.View SolutionQuestion 116
A truck is moving with a constant velocity of 54kmh−1. In which direction (angle with the direction of motion of truck) should a stone be projected up with a velocity of 20ms−1, from the floor of the truck of the truck, so as to appear at right angles to the truck, for a person standing on earth ?View SolutionQuestion 117
A river flows with a speed more than the maximum speed with which a person can swim in still water. He intends to cross the river by the shortest possible path (i.e., he wants to reach the point on the opposite bank which directly opposite to the starting point). Which of the following is correct ?View SolutionQuestion 131
A ball is thrown from a point with a speed 'v^(0)' at an elevation angle of θ . From the same point and at the same instant , a person starts running with a constant speed 'v0'2 to catch the ball . Will the person be able to catch the ball ? If yes, what should be the angle of projection θ ? View SolutionQuestion 148
A person sitting in the rear end of the compartment throws a ball towards the front end. The ball follows a parabolic path. The train is moving with uniform velocity of 20ms−1. A person standing outside on the ground also observers the ball. How will the maximum heights (hm) attained and the ranges (R) seen by thrower and the outside observer compare each other?View SolutionQuestion 156
A body is projected up a smooth inclined plane with velocity V from the point A as shown in the figure. The angle of inclination is 45∘ and the top is connected to a well of diameter 40m. If the body just manages to across the well, what is the value of V? Length of inclined plane is 20√2m.
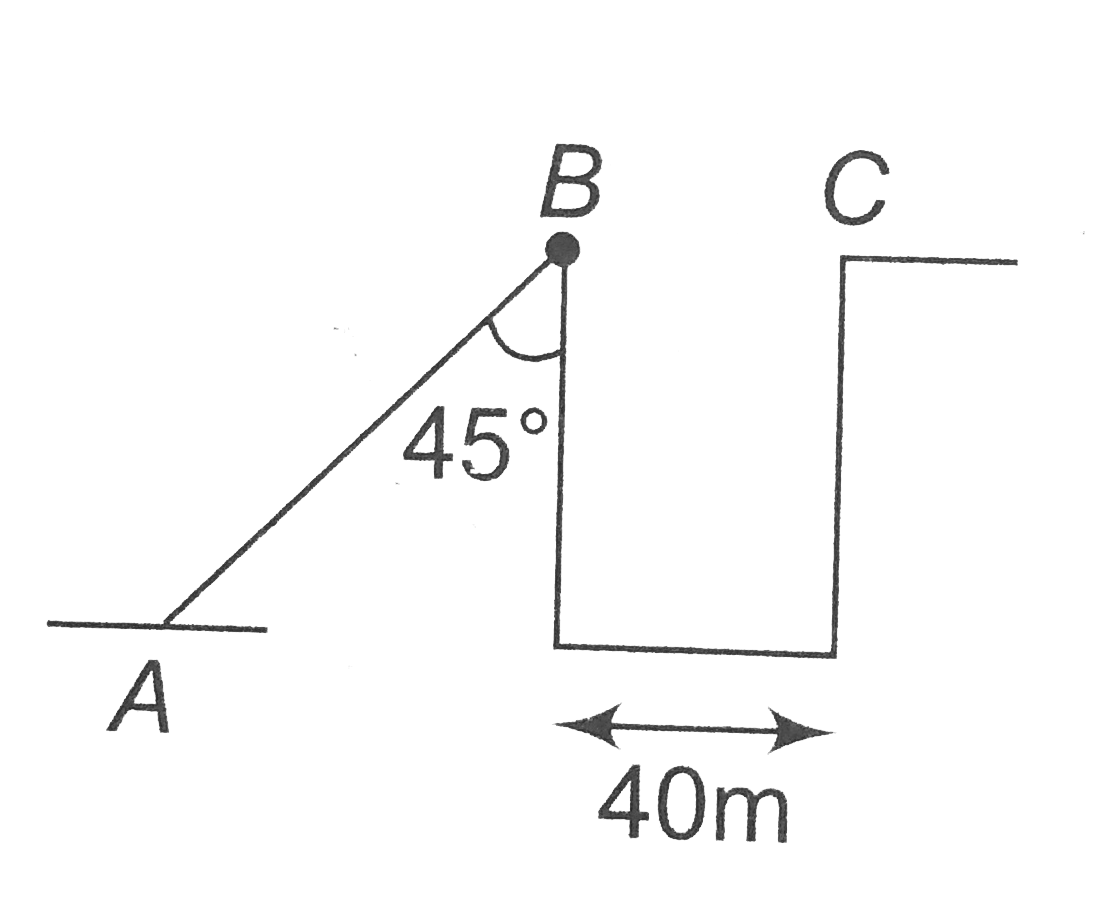 View Solution
View SolutionQuestion 162
The trajectory of a projectile in a vertical plane is y=ax−bx2, where aandb are constant and xandy are, respectively, horizontal and vertical distances of the projectile from the point of projection. The maximum height attained by the particle and the angle of projectile from the horizontal are.View SolutionQuestion 166
A body of mass m is projected horizontally with a velocity v from the top of a tower of height h and it reaches the ground at a distance x from the foot of the tower. If a second body of mass 2m is projected horizontally from the top of a tower of height 2h, it reaches the ground at a distance 2x from the foot of the tower. The horizontal velocity of the second body is :View SolutionQuestion 173
A particle P is projected with velocity u1 at an angle of 30∘ with the horizontal. Another particle Q is thrown vertically upwards with velocity u2 from a point vertically below the highest point of path of P. Determine the necessary condition for the two particles to collide at the highest point.
 .View Solution
.View SolutionQuestion 182
Two cities AandB are connected by a regular bus service with buses plying in either direction every T seconds. The speed of each bus is uniform and equal to Vb. A cyclist cycles from A→B with a uniform speed of Vc. A bus goes past the cyclist in T1 second in the direction A→B and every T2 second in the direction B→A. ThenView SolutionQuestion 186
A particle is dropped from a tower in a uniform gravitational field at t=0. The particle is blown over by a horizontal wind with constant velocity. The slope (m) of the trajectory of the particle with horizontal and its kinetic energy vary according to curves. Here, x is the horizontal displacement and h is the height of particle from ground at time t.View SolutionQuestion 194
In a plane projectile motion, the angle between instantaneous velocity vector and acceleration vertor can be anything between 0orπ (excluding the limiting case).
In plane-to-plane projectile motion, accleration vector is always pointing vertical downwards. (neglect air friction).View SolutionQuestion 196
A car is moving towards south with a speed of 20ms−1. A motorcyclist is moving towards east with a speed of 15s−1. At a certain instant, the motorcyclist is due south of the car and is at a distance of 50mfrom the car.
The shortest distance between the motorcyclist and the car is.View SolutionQuestion 199
A man can swim at a speed of 3kmh−1 in still water. He wants to cross a 500−m wide river flowing at 2kmh−1. He keeps himself always at an angle to 120∘ with the river flow while swimming.
The drift of the man along the direction of flow, when he arrives at the opposite bank is.View SolutionQuestion 214
A particle is projected with a speed u at angle θ with the horizontal. Consider a small part of its path near the highest position and take it approximately to be a circular arc. What is the radius of this circle? This radius is called the adius of curvature of the curve at the point.View Solution
 .
. .
. .
.
 .
. .
. .
. .
. .
. .
. .
. .
. .
.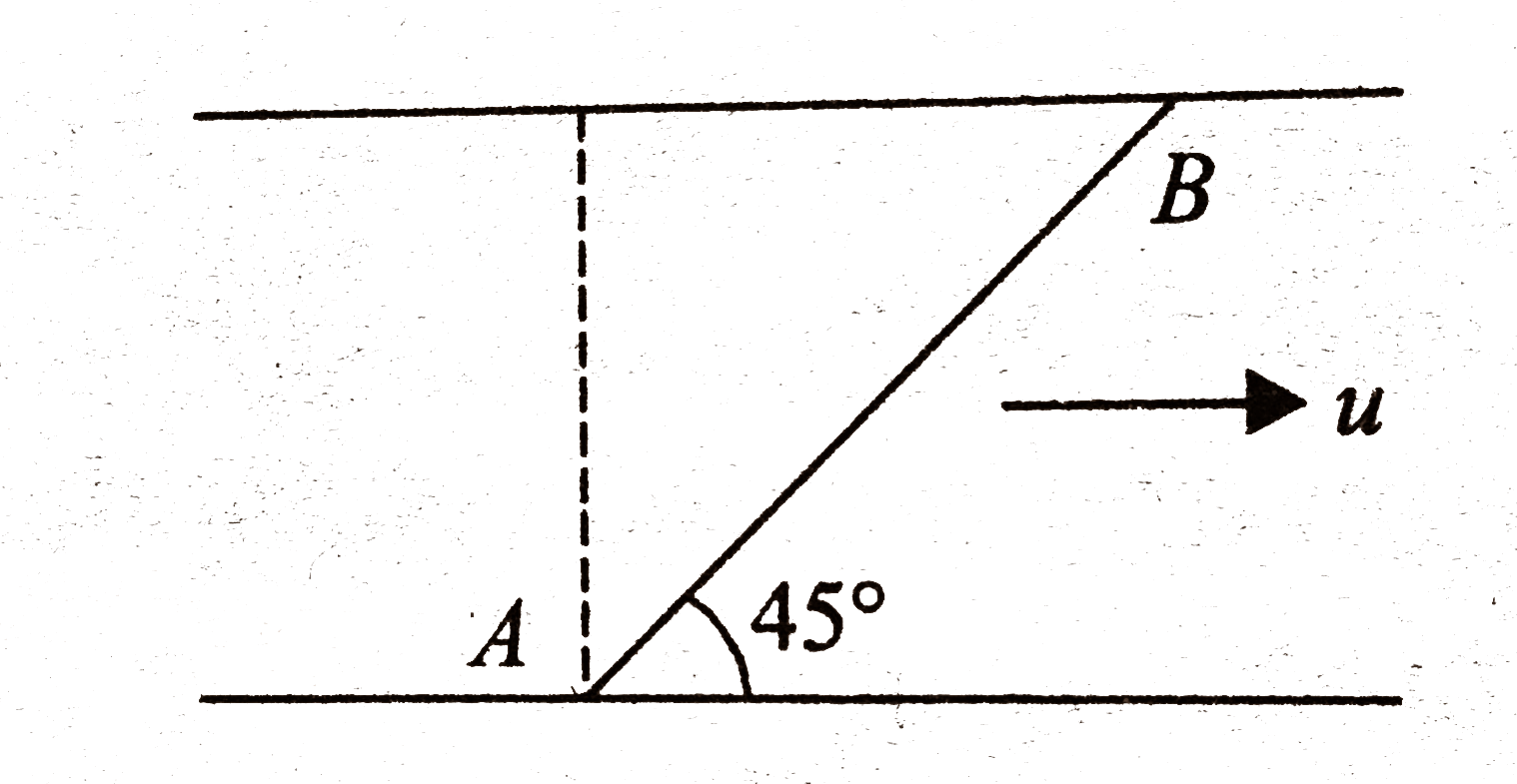 .
.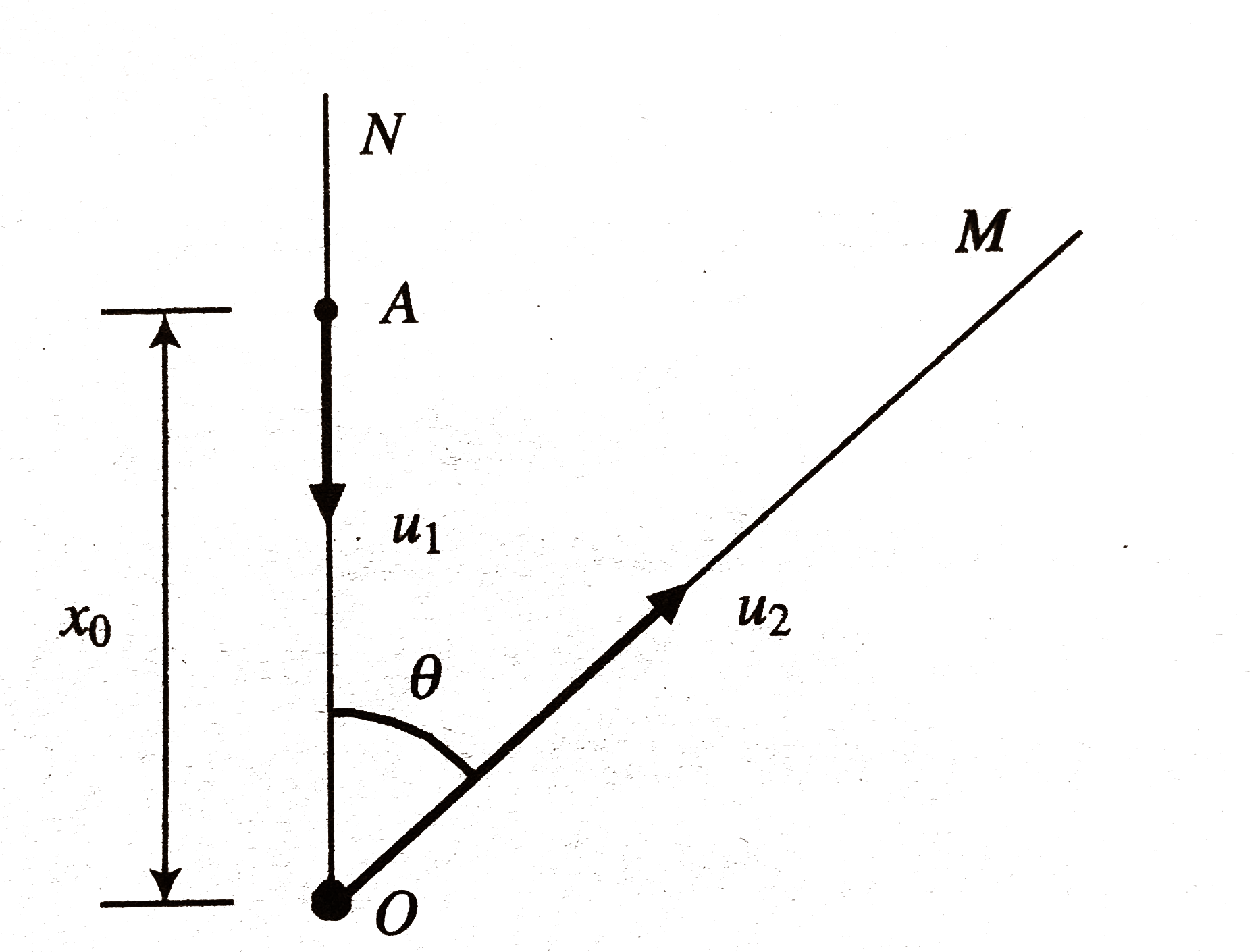 .
. .
. .
. .
.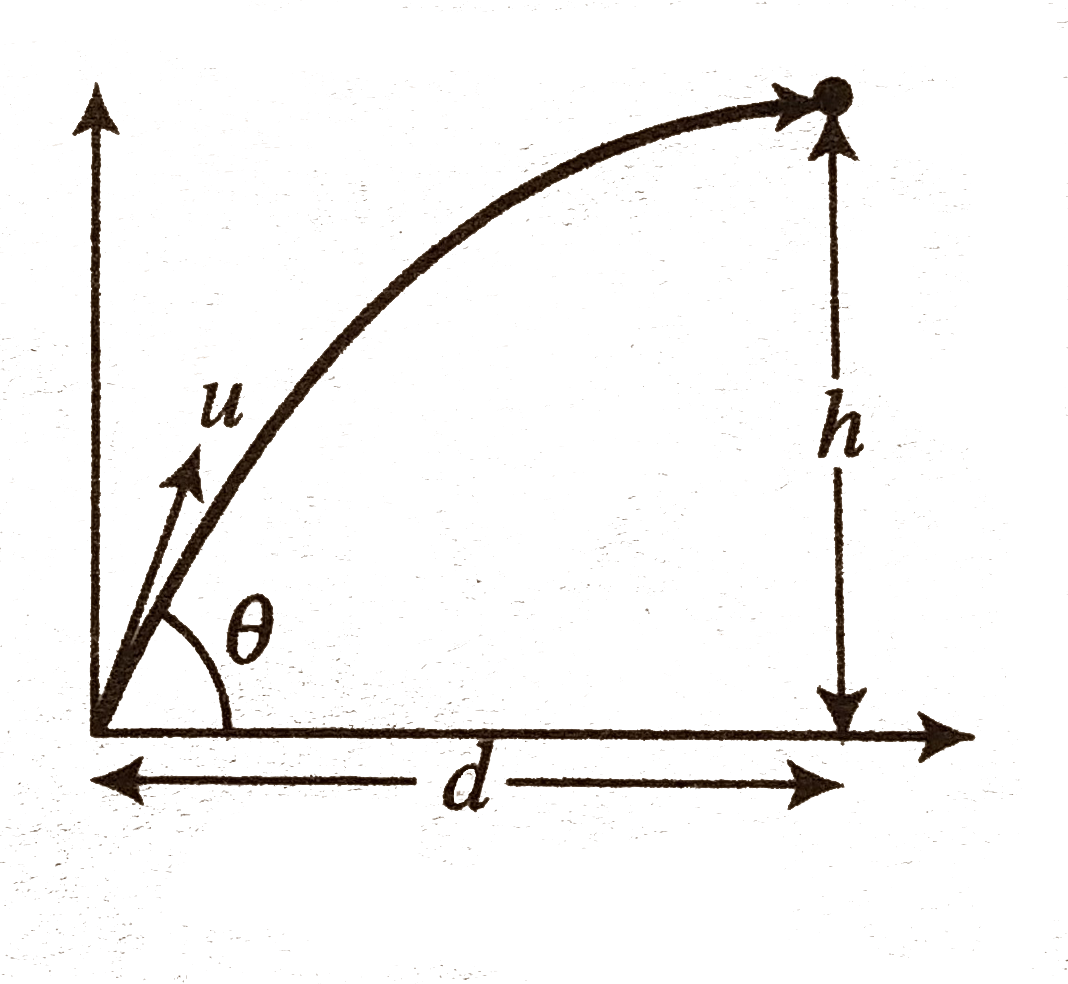 .
. .
.
 .
. .
. .
.

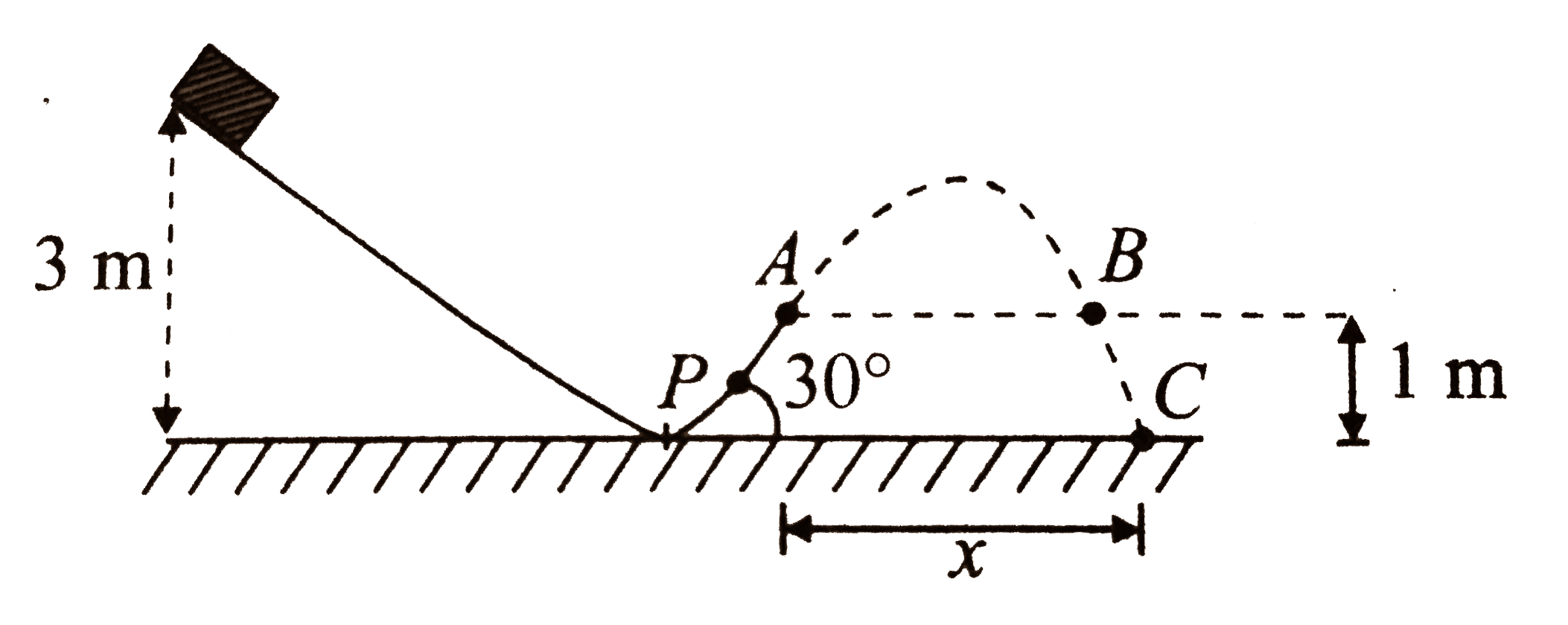 .
. 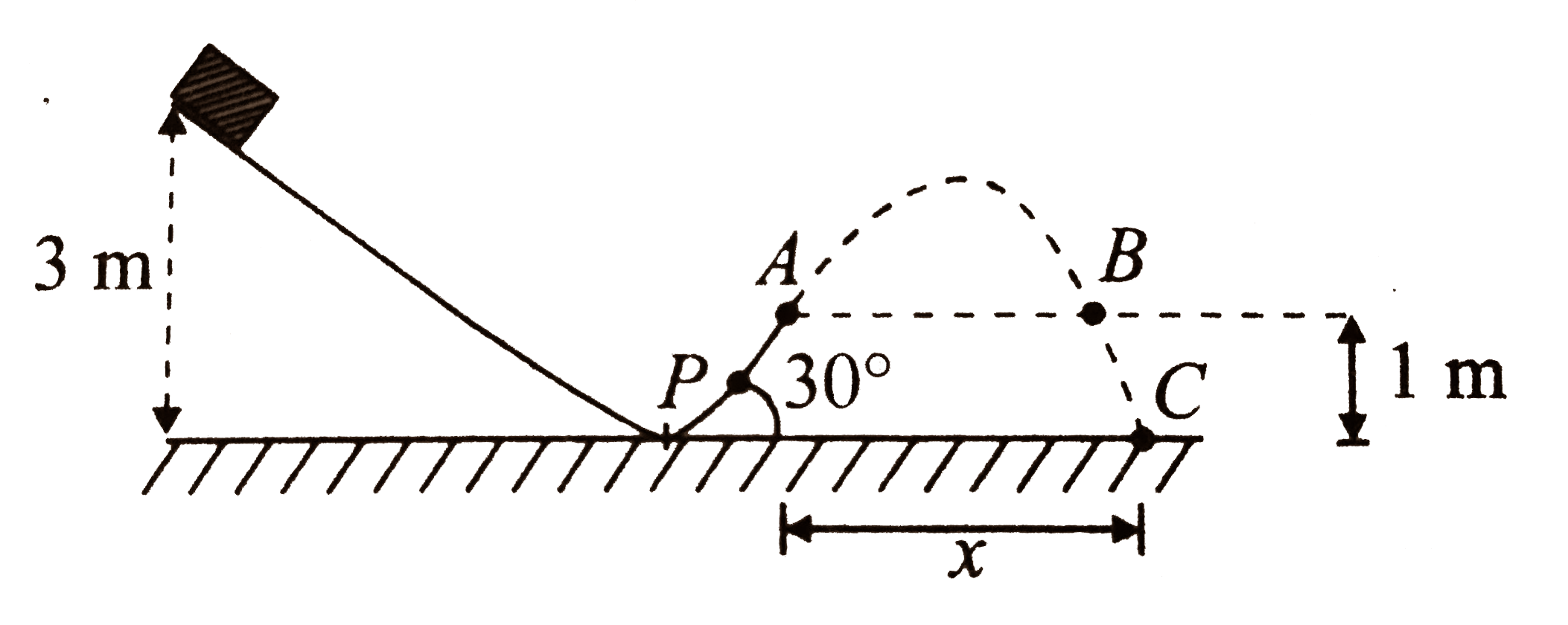 .
. 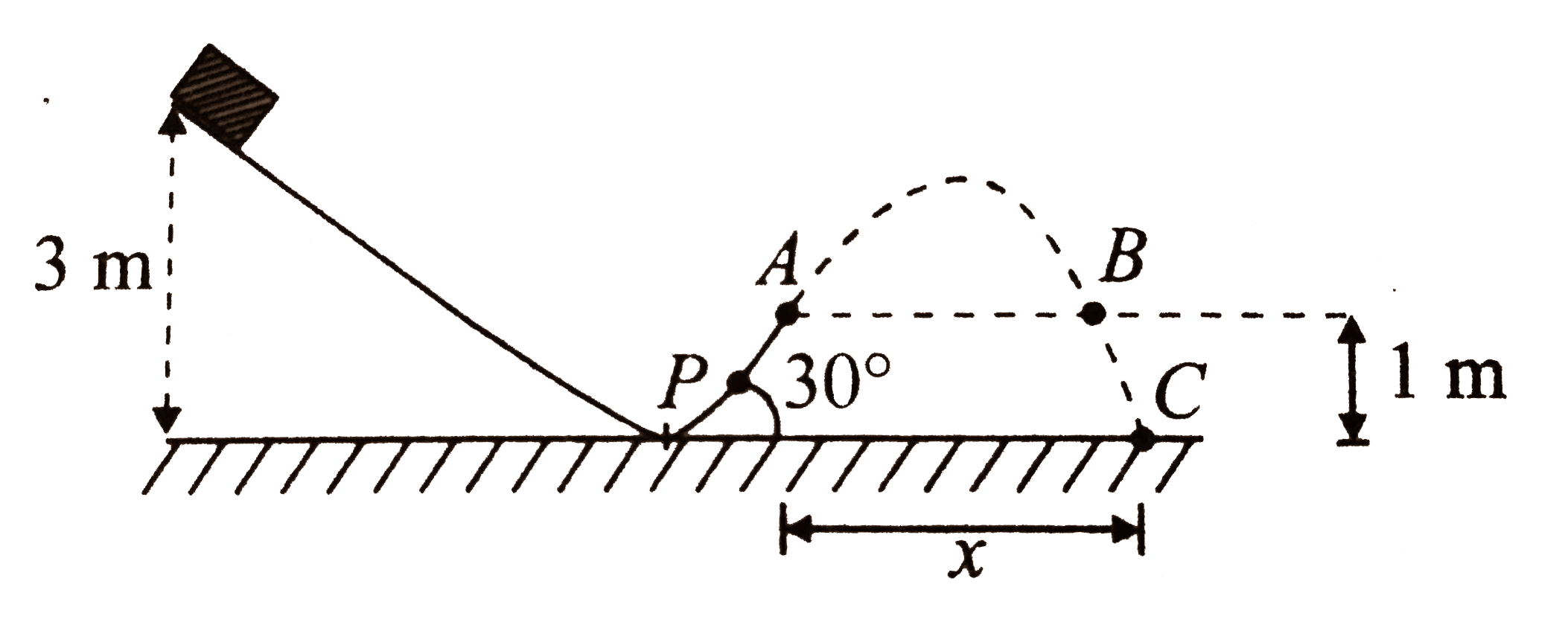 .
. 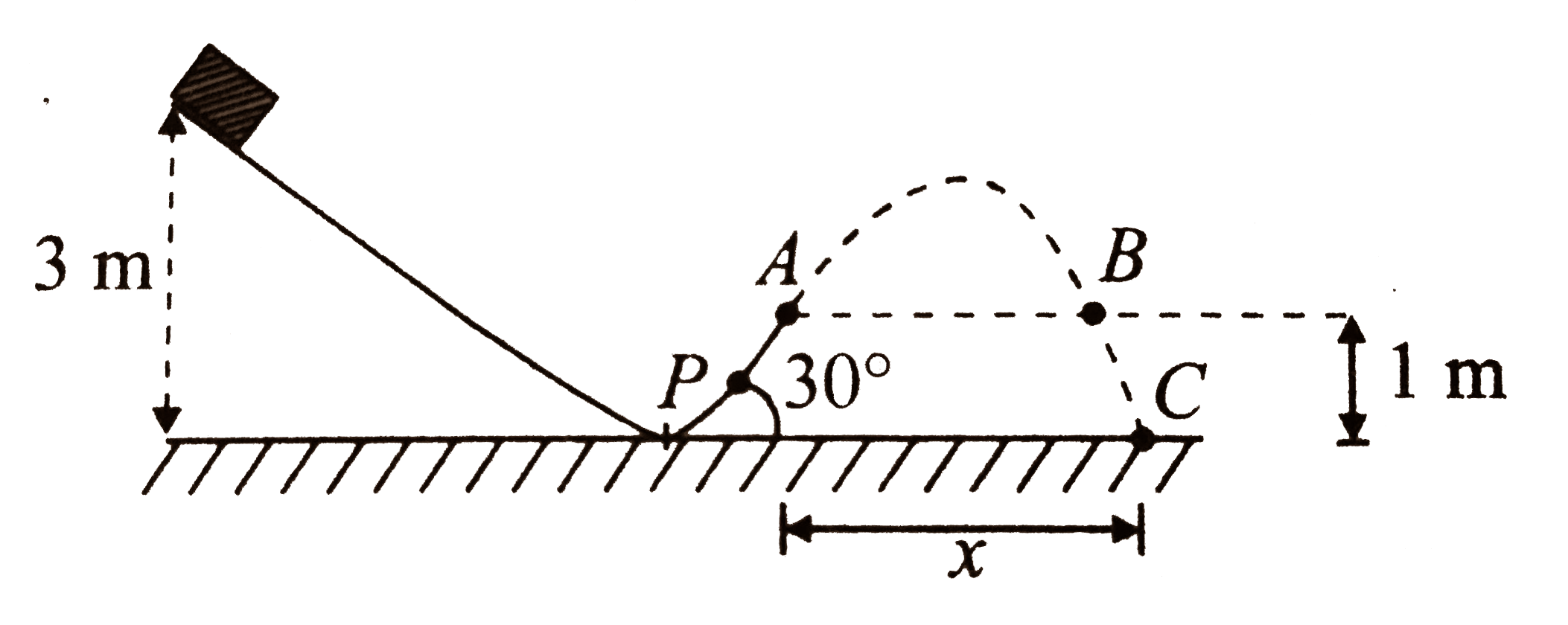 .
. 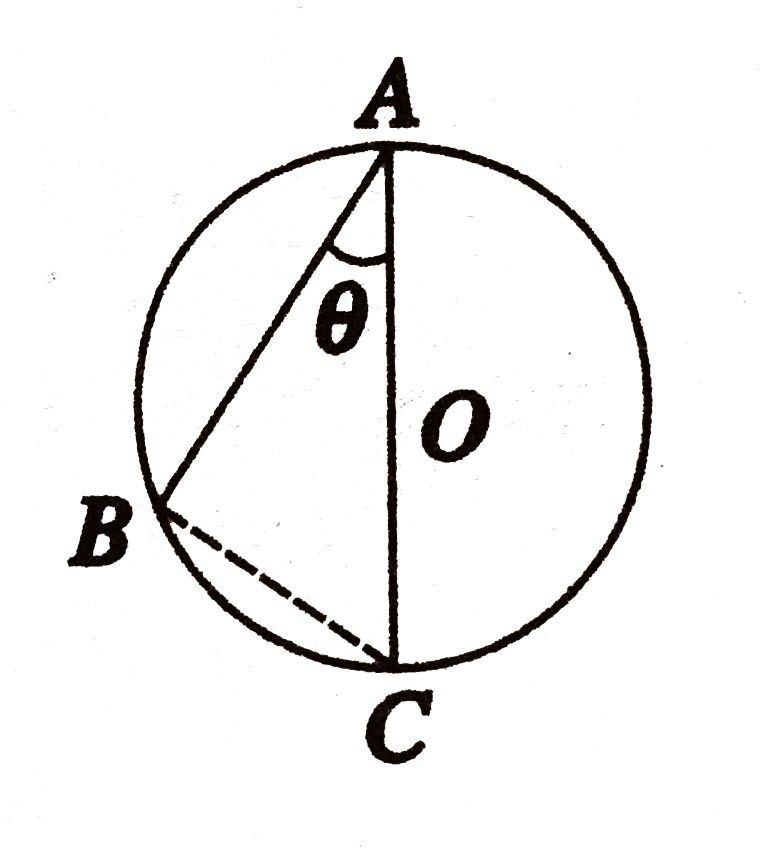 .
.