The First Law Of Thermodynamics - Heat Capacity from IE IRODOV PHYSICS (HINGLISH) THERMODYNAMICS AND MOLECULAR PHYSICS for Class 12
| Class 12 | PHYSICS |
| Chapter | THERMODYNAMICS AND MOLECULAR PHYSICS |
| IE IRODOV PHYSICS (HINGLISH) | The First Law Of Thermodynamics - Heat Capacity |
| Medium | English |
| Academic Year | 2023-2024 |
Question 1
A vessel of volume V=301 contains ideal gas at the temperature 0∘C. After a portion of the gas has been let out, the pressure in the vessel decreased by Δp=0.78atm (the temperature remaining constant). Find the mass of the released gas. The gas density under the normal conditions ρ=1.3g/1.View SolutionQuestion 2
Two identical vessels are connected by a tube with a valve letting the gas from one vessel into the other if the pressure difference Δp≥1.10atm. Initially there was a vacuum in one vessel while the other contained ideal gas at a temperature t1=27∘C and pressure p1=1.00atm. Then both vessels were heated to a temperature t2=10.7∘C. Up to what value will the pressure in the first vessel (which had vacuum initially) increase ?View SolutionQuestion 5
A vessel of volume V=7.51 contains a mixture of ideal gases at a temperature T=300K:v1=0.10 mole of oxygen, v2=0.20 mole of nitrogen, and v3=0.30 mole of carbon dioxide. Assuming the gases to be ideal, find :
(a) the pressure of the mixture ,
(b) the mean molar mass M of the given mixture which enters its equation of state pV=(m/M)RT, where m is the mass of the mixture.View SolutionQuestion 6
A vertical cylinder closed from both ends is equipped with an easily moving piston dividing the volume into two parts, each containing one mole of air. In equilibrium at T0=300K the volume of the upper part is η=4.0 times greater than that of the lower part. At what temperature will the ratio of these volumes be equal to η'=3.0 ?View SolutionQuestion 8
Find the pressure of air in a vessel being evacuated as a function of evacuation time t. The vessel volume is V, the initial pressure is p0. The process is assumed to be isothermal, and the evacuation rate equal to C and independent of pressure.
The evatuation rate is the gas volume being evacuated per unit time, with that volume being measured under the gas pressure attained by that moment.View SolutionQuestion 10
A smooth vertical tube having two different cross sections is open from both the ends but closed by two sliding pistions as shown in Fig. and tied with an inextensible string. One mole of an ideal gas is enclosed between the piston The difference in cross-sectional areas of the two pistons is given ΔS. The masses of piston are m1 and m2 for larger and smaller one, respectively. Find the temperature by which tube is raised so that the pistons will be displaced by a distance l. Take atmospheric pressure equal to P0
View SolutionQuestion 13
A tall cylindrical vessel with gaseous nitrogen is located in a uniform gravitational field in which the free-fall acceleration is equal to g. The temperature of the nitrogen varies along the height h so that its density is the same throught the volume. find the temperature gradient dT/dh.View SolutionQuestion 15
Let us assume that air is under standard conditions close to the Earth's surface. Presuming that the temperature and the molar mass of air are independent of height, find the air pressure at the height 5.0km over the surface and in a mine at the depth 5.0km below the surface.View SolutionQuestion 17
An ideal gas of molar mass M is contained in a tall vertical cylindrical vessel whose base area is S and height h. The temperatuer of the gas is T, its pressure on the bottom bass is p0. Assuming the temperature and the free-fall acceleration g to be independent of the height, find the mass of gas in the vessel.View SolutionQuestion 19
An ideal gas of molar mass M is located in the uniform gravitational field in which the free-fall acceleration is equal to g. Find the gas pressure as a function of height h. If p=p0 at h=0, and the temperature varies with height as
(a) T=T0(1−ah) ,
(b) T=T0(1+ah),
where a is a positive constant.View SolutionQuestion 20
A horizontal cylinder closed from one end is rotated with a constant angular velocity ω about a vertical axis passing through the open end of the cylinder. The outside air pressure is equal to p0, the temperature to T, and the molar mass of air to M. find the air pressure as a function of the distance r from the rotate axis. The molar mass is assumed to be independent of r.View SolutionQuestion 22
One mole of nitrogen is contained in a vessel of volume V=1.001. Find :
(a) the temperature of the nitrogen at which the pressure can be calculated from an ideal gas law with an error η=10% (as compared with the pressure calculated from the Van der Walls equation of state) ,
(b) the gas pressure at this temperature.View SolutionQuestion 28
Two vessels of volume (V1)and(V2) contain the same ideal gas. The pressures in the vessels are (P1)and(P2) and the temperatures are (T1)and(T2) respectively . The two vessels are now connected to each other through a narrow tube. Assuming that no heat is exchanged between the surrounding and the vessels, find the common pressure and temperature attained after the connection. View SolutionQuestion 32
Two moles of a certain gas at a temperature T0=300K were cooled isochorically so that the pressure of the gas got reduced 2 times. Then as a result of isobaric process, the gas is allowed to expand till its temperature got back to the initial value. Find the total amount of heat absorbed by gas in this process.View SolutionQuestion 35
One mole of a certain ideal gas is contained under a weight-less piston of a vertical cylinder at a temperature T. The space over the piston opens into the atmosphere. What work has to be performed on order to increase isothermally the gas volume under the piston n times by slowly raising the piston ? The friction of the piston against the cylinder walls is negligibly small.View SolutionQuestion 36
A piston can freely move inside a horizontal cylinder closed from both ends. Initially, the piston separates the inside space of the cylinder into two equal parts each of volmek V0 in which an ideal gas is contained under the same pressure p0 and at the same temperature. What work has to be performed in order to increase isothermally the volume of one part of gas η times compared to that of the other by slowly moving the piston ?View SolutionQuestion 37
Three moles of an ideal gas being initially at a temperature Ti=273K were isothermally expanded 5 times its initial volume and then isochorically heated so that the pressure in the final state becomes equal to that in the initial state. The total heat supplied in the process is 80kJ. Find γ(=CpCV) of the gas.View SolutionQuestion 41
A heat-conducting piston can freely move inside a closed thermally insulated cylinder with an ideal gas. In equilibrium the piston divides the cylinder into two equal parts, the gas temperature being equal to T0. The piston is slowly displaced. Find the gas temperature as a function of the ratio η of the volumes of the greater and smaller sections. The adiabatic exponent of the gas is equal to γ.View SolutionQuestion 47
On mole of argon expands polytropically, the polytropic constant being 1.5, that is, the process proceeds according to the law pV1.5 = constant. In the process, its temperature change by ΔT=−26K. Find
a. the amount of heat obatined by the gas.
b. the work performed by the gas.View SolutionQuestion 48
An ideal gas whose adiabatic exponent equals γ is expanded according to the law p=αV, where α is a constant. The initial volume of the gas is equal to V0. As a result of expansion the volume increases η times. Find :
(a) The incident of the internal energy of the gas ,
(b) the work performed by the gas ,
( c) the molar heat capacity of the gas in the process.View SolutionQuestion 49
An ideal gas whose adiabatic exponent equals γ is expanded so that the amount of heat transferred to the gas is equal to the decrease of its internal energy. Find :
(a) the molar heat capacity of the gas in the process ,
The equation of the process in the variables t,V ,
( c) the work performed by one mole of the gas when its volume increases η times if the initial temperature of the gas is T0.View SolutionQuestion 50
One mole of an ideal gas whose adiabatic axponent equal γ undergoes a process in which the gas pressure relates to the temperature as p=aTα, where a and α are consists. Find :
(a) the work performed by the gas if its temperature gets an increment ΔT ,
(b) the molar heat capacity of the gas in the process , at what value of α will the heat capacity be negative ?View SolutionQuestion 51
An ideal gas with the adiabatic exponent γ undergoes a process in which its internal energy relates to the volume as u=aVα. Where a and α are constants. Find :
(a) the work performed by the gas and the amount of heat to be transferred to this gas to increase its internal energy by ΔU ,
(b) the molar heat capacity of the gas in this process.View SolutionQuestion 53
One mole an ideal gas whose adiabatic exponent equals γ undergoes a process p=p0+α/V, where p0 and α are positive constants. Find :
(a) heat capacity of the gas as a function of its volume ,
(b) the internal energy of heat transferred to the gas, of its volume increased from V1 to V2.View SolutionQuestion 54
One mole of an ideal gas with heat capacity at constant pressure Cp undergoes the process T=T0+αV, where T0 and α are constants. Find :
(a) heat capacity of the gas as a function of its volume ,
(b) the amount of heat transferred to the gas, if its volume increased from V1 to V2.View SolutionQuestion 56
An ideal gas has an adiabatic exponent γ. In some process its molar heat capacity varies as C=α/T,where α is a constant Find :
(a) the work performed by one mole of the gas during its heating from the temperature T0 to the temperature η times higher ,
(b) the equation of the process in the variables p,V.View SolutionQuestion 60
Two thermally insulated vessels are interconnected by a tube equipped with a valve. One vessel volume V1=101 contains v=2.5 moles of carbon dioxide. The other vessel of volume V1=1001 is evacuated. The valve having been opened, the gas adiabatically expanded. Assuming the gas to obey the Van der Walls equation, find its temperature change accompanying the expansion.View SolutionQuestion 65
A parallel beam of nitrogen molecules moving with velocity v=400ms−1 imprings on a wall at an angle θ=30∘ to its normal. The concentration of molecules in the beam is n=9×1018cm−3. Find the pressure exerted by the beam on the wall, assuming that collisions are perfectly elastic.View SolutionQuestion 69
Suppose a gas is heated up to a temperature at which all degrees of freedom (translational, rotational, and vibrational) of its molecules are excited. Find the molar heat capacity of such a gas in the isochoric process, as well as the adiabatic exponent γ, if the gas consists of
(a) diatomic ,
(b) linear N−atomic ,
( c) network N−atomic molecules.View SolutionQuestion 70
An ideal gas consisting of N−atomic molecules is expanded isobarically. Assuming that all degrees of freedom (translational, rotational, and vibrational) of the molecules are excited, find what fraction of heat transferred to the gas in this process is spend to perform the work of expansion. Now high is this fraction in the case of monatomic gas ?View SolutionQuestion 86
In the case of gaseous nitrogen find :
(a) the temperature at which the velocities of the molecules v1=300m/s and v2=600m/s are associated with equal values of the Maxwell distribution friction F(v) ,
(b) the velocity of the molecules v at which the value of the Maxwell distribution function F(v) for the temperature T0 will be the same as that for the temperature η times higher.View SolutionQuestion 96
A gas consists of molecules of mass m and is at a temperature T. Making use of the Maxwell velocity distribution function, find the corresponding distribution of the molecules over the kinetic energies ε. Determine the most probable value of a gas the kinetic energy εp. Does εp correspond to the most probable velocity ?View SolutionQuestion 99
The velocity distribution of molecules in a beam coming out of a hole in a vessel is described by the function F(v)=Av3e−mv2/2kT, where T is the temperature of the gas in the vessel. Find the most probable values of
(a) the velocity of the molecules in the beam , compare the result obtained with the most probable velocity of the molecules in the vessel ,
(b) the kinetic energy of the molecules in the beam.View SolutionQuestion 104
Suppose that η0 is the ratio of the molecular concentration of hydrogen to that of nitrogen at the Earth's surface, while η is the corresponding ratio at the height h=3000m. Find the ratio η/η0 at the temperature T=280K, assuming that the temperature and the free fall acceleration are independent of the height.View SolutionQuestion 105
A tall vertical vessel contains a gas composed of two kinds of molecules of masses m1 and m2 . With m2>m1. The concentrations of these molecules at the bottom of the vessel are equal to n1 and n2 respectively, with n2>n1. Assuming the temperature T and the free-fall acceleration g to be independent of the height, find the height at which the concentrations of these kinds of molecules are equal.View SolutionQuestion 107
A very tall vertical cylinder contains a gas at a temperature true T. Assuming the gravitational field to be uniform, find the mean value of the potential energy of the gas molecules. Does this value depend on whether the gas consists of one kind of molecules or of serveral kinds ?View SolutionQuestion 109
Find the mass of a mole of colloid particles if during their centrifuging with an angular velocity ω about a vertical axis the concentration of the particles at the distance r2 from the rotation axis is η times greater than that at the distance r1 (in the same horizontal plane). The densities of the particles and the solvent are equal to ρ and to ρ0 respectively.View SolutionQuestion 110
A horizontal tube with closed ends is rotated with a constant angular velocity ω about a vertical axis passing through one of its ends. The tube contains carbon dioxide at a temperature T=300K. The length of the tube is l=100cm. Find the value ω at which the ratio of molecular concentrations at the opposite ends of the tube is equal to η=2.0.View SolutionQuestion 111
The potential energy of gas molecules in a certain certral field depends on the distance r from the field's centre as u(r)=ar, where a is a positive constant. The gas temperature is T, the concentration of molecules at the centre of the field is n0 Find :
(a) the number of molecules located at the distances between r and r+dr from the centre of the field ,
(b) the most probable distance separating the molecules from the centre of the field ,
( c) the fraction of molecules located in the spherical layer between r and r+dr ,
(d) how many times the concentration of molecules in the centre of the field will change if the temperature decreases η times.View SolutionQuestion 112
From the conditions of the foregoing problem find :
(a) the number of molecules whose potential energy lies within the internal from U to U+dU ,
(b) the most probable value of the potential energy of a molecule , compare this value with the potential energy of a molecule located at its most probable distance from the centre of the field.View SolutionQuestion 116
An ideal gas goes through a cycle consisting of alternate isothermal and adiabatic curves (Fig. 2.2). The isothermal processes proceed at the temperatures T1,T2 and T3. Find the efficiency of such a cycle, if in each isothermal expansion the gas volume increases in the same alphaortion.
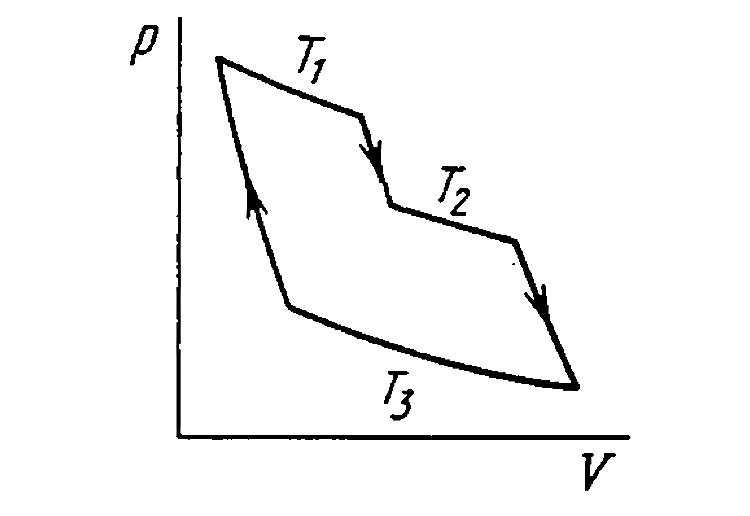.View SolutionQuestion 120
An ideal gas goes through a cycle consisting of
(a) isochoric, adiabatic, and isothermal lines ,
(b) isobaric, adiabatic, and isothermal lines,
with the isothermal process proceeding at the minimum temperature of the whole cycle. Find the efficiency of each cycle if the absolute temperature varies n−fold within the cycle.View SolutionQuestion 139
One mole of an ideal gas goes through a process in which the entropy of the gas changes with temperature T as S=aT+CV1nT, where a is a positive constant. CV is the molar heat capacity of this gas at constant volume. Find the volume dependence of the gas temperature in this process if T=T0 at V=V0.View SolutionQuestion 146
One mole of an ideal gas with heat capacity CV goes through a process in which its entropy S depends on T as S=α/T, where α is a constant. The gas temperature varies from T1 to T2 Find :
(a) the molar heat capacity of the gas as function of its temperature ,
(b) the amount of heat transferred to the gas ,
( c) the work performed by the gas.View SolutionQuestion 149
A weightless piston divides a thermally insulated cylinder into two equal parts. One part contains one mole of an ideal gas with adiabatic exponent γ, the other is evacuated. The initial gas temperature is T0. The piston is released and the gas fills the whole volume of the cylinder. Then the piston is slowly displaced back to the initial position. Find the increment of the internal energy and entropy of the gas was resulting from these two processes.View SolutionQuestion 151
A thermally insulated vessel is partitioned into two parts so that the volume of one part is n=2.0 times greater than that of the other. The smaller part contains v1=0.30 mole of nitrogen, and the greater one v2=0.70 mole of oxygen. The temperature of the gases is the same. A hole is punctured in the partition and the gases are mixed. Find the corresponding increment of the system's entropy, assuming the gases to be ideal.View SolutionQuestion 152
A piece of copper of mass m1=300g with initial temperature t1=97∘C is placed into a calorimeter in which the water of mass m2=100g is at a temperature t2=7∘C. Find the entropy increment of the system by the moment the temperature t2=7∘C. FInd the entropy increment of the system by the moment the temperatures equalize. The heat capacity of the calorimeter itself is negligibly small.View SolutionQuestion 153
Two identical thermally insulated vessels interconnected by a tube with a valve contain one mole of the same ideal gas each. The gas temperature in one vessel is equal to T1 and in the other, T2. The molar heat capacity of the gas of constant volume equals Cv. the valve having been opened, the gas comes to a new equilibrium state. Find the entropy increment ΔS of the gas. Demonstrate that ΔS>0.View SolutionQuestion 154
N atoms of gaseous helium are enclosed in a cubic vessel of volume 1.0cm3 at room temperature. Find :
(a) the probability of atoms gathering in one half of the vesse ,
(b) the approximate numerical value of N ensuring the occurrence of this event within the time interval ≈1010 years (the age of the Universe).View SolutionQuestion 164
The diameter of an air-bubble formed at the bottom of a pond is d=4μm, when the bubble rises to the surface, its diameter increases n=1.1 times. If expansion of air bubble is assumed to be isothermal and atmospheric pressure to be standard. How deep the pond at the spot is [surface tension of water 0.075Nm]View SolutionQuestion 167
A galss capillary length l=11cm and inside diameter d=20μm is submerged vertically into water. The upper end of the capillary is sealed. The outside pressure is considered to be 1×105Nm2 . To what length has the capillary to be submerged to make the water levels inside and outside the capillary coincide?View SolutionQuestion 168
When a vertical capillary of length l with a sealed upper end was brought in contact with the surface of a liquid, the level of this liquid rose to the height h. The liquid density is ρ, the inside diameter the capillary is d, the contact angle is θ, the atmospheric pressure is ρ0. Find the surface tension of the liquid. (Temperature in this process remains constant.)
View SolutionQuestion 169
A glass rod of diameter d1=1.5mm in inserted symmetrically into a glass capillary with inside diameter d2=2.0 mm. Then the whole arrangement is vertically oriented and brought in contact with the surface of water. To what height will the liquid rise in the capillary?
Surface tension of water =73×10−3N/mView SolutionQuestion 170
Two vertical plates submerged partially in a wetting liquid form a wedge with a very small angle δφ. The edge of this wedge is vertical. The density of the liquid is ρ, its surface tension is α, the contact angle is θ. Find the height h, to which the liquid rises, as a function of the distance x from the edge.View SolutionQuestion 171
A vertical water jet flows out of a round hole. One of the horizontal sections of the jet has the diameter d=2.0mm while the other section section located l=20mm lower has the diameter which is n=1.5 times less. Find the volume of the water flowing from the hole each second.View SolutionQuestion 173
A mercury drop shaped as a round tablet of radius R and and thickness h is located between two horizontal glass plates. Assuming that h<<R, find the mass m of a weight which has to be placed on the upper plate to diminish the distance between the plates n-times. The contact angle equals θ. Calculate m if R=2.0cm,h=0.38mm,n=2.0, and θ=135∘.View SolutionQuestion 176
Two vertical parallel glass plates are partically submerged in water. The distance between the plates is d=0.10mm, and their width is l=12cm assuming that the water between the plates does not reach the upper edges of the plates and the wetting is complete. Find the force of their mutual attractionView SolutionQuestion 182
A soap bubble of radius r is inflated with an ideal gas. The atmospheric pressure is p0, the surface tension of the soap water solution is α. Find the difference between the molar heat capacity of the gas during its heating inside the bubble and the molar heat capacity of the gas under constant pressure, C−Cp.View SolutionQuestion 184
The surface of a soap film was increasedd isothermallly by Δo at a temperature T. Knowing the surface tension of the soap water solution α and the temperature coefficient dα/dT, find the increment.
(a) of the entropy of the film's surface layer ,
(b) of the internal energy of the surface layer.View SolutionQuestion 185
A saturated water vapour is contained in a cylindrical vessel under a weightless piston at a temperature t=100∘C. As a result of a slow introduction of the piston a small fraction of the vapour Δm=0.70g gets condensed. What amount of work was perfomed over the gas ? The vapour is assumed to be ideal, the volume of the liquid is to be neglected.View SolutionQuestion 186
A vessel of volume V=6.01 contains water together with its saturated vapour under a pressure of 40atm and at a temperature of 250∘C. The specific volume of the vapour is equal to V'v=501/kg under these conditions. The total mass of the system water-vapour equals m=5.0kg. Find the mass and the volume of the vapour.View SolutionQuestion 187
The saturated water vapour is inclosed in a cylinder under a piston and occupies a volume V0=5.01 at the temperature t=100∘C. Find the mass of the liquid phase formed after the volume under the piston decreased isothermally to V=1.61. The saturated vapour is assumed to be ideal.View SolutionQuestion 188
A volume occupied by a saturated vapour is reduced isothermally n−fold. Find what fraction η of the final volume is occupied by the liquid phase if the specific volumes of the saturated vapour and the liquid phase differ by N times (N>n). Solve the same problem under the condition that the final volume of the substance corresponds to the midpoint of a horizontal portion of the isothermal line in the diagram p,V.View SolutionQuestion 190
Water of mass m=20g is enclosed in a thermally insulated cylinder at the temperature of 0∘C under a weightless piston whose area is S=410cm2. The outside pressure is equal to standard atmospheric pressure. To what height will the piston rise when the water absorbs Q=20.0kJ of heat ?View SolutionQuestion 191
One gram of saturated water vapour is enclosed in a thermally insulated cylinder ubder a weightless piston. The outside pressure being standard, m=1.0g of water is introduced into the cylinder at a temperature t0=22∘C. Neglecting the heat capacity of the cylinder and the friction of the piston against the cylinder's walls, find the work performed by the force of the atmospheric pressure during the lowering of the piston.View SolutionQuestion 192
If an additional pressure Δp of a saturated vapour over a convex spherical surface of a liquid is considerably less than the vapour pressure over a plane surface, then Δp=(ρv/ρl)2α/r, where ρv and ρl) are the densities of the vapour and the liquid, α is the surface tension, and r is the radius of curvature of the surface. Using this formula, find the diameter of water droplets at which the saturated vapour pressure exceeds the vapour pressure over the plane surface by η=1.0% at a temperature t=27∘C. The vapour is assumed to be an ideal gas.View SolutionQuestion 196
Find the internal pressure pi of a liquid if its density ρ and specific latent heat of vaporization q are known. The heat q is assumed to be equal to the work performed against the forces of the internal pressure, and the liquid obeys the Van der Waals equation. Calculate pi in water.View SolutionQuestion 200
Write the Van der Waals equation via the reduced parameters π,v and τ, having taken the corresponding critical values for the units of pressure, volume, and temperature. Using the equation obtained, find how many times the gas temperature exceeds its critical temperature if the gas pressure is 12 times as high as critical pressure, and the volume of gas is equal to half the critical volume.View SolutionQuestion 209
A small amount of water and its saturated vapour are enclosed in a vessel at a temperature t=100∘C. How much (in per cent) will the mass of the saturated vapour increase if the temperature of the system goes up by ΔT=1.5K ? Assume that the vapour is an ideal gas and the specific volume of water is negligible as compared to that vapour.View SolutionQuestion 210
Find the pressure of saturated vapour as a function of temperature p(τ) if a temperature T0 its pressure equals p0. Assume that : the specific latent heat of vaporization q is independent of T, the specific volume of liquid is negligible as compared to that of vapour, saturated vapour obeys the equation of state for an ideal gas. Investigate under what conditions these assumptions are permissible.View SolutionQuestion 211
An ice which was initially under standard conditions was compressedup to the pressure p=640atm. Assuming the lowering of the ice melting temperature to be a linear function of pressure under the given conditions, find what fraction of the ice melted. The specific volume of water is less than of ice by ΔV'=0.09cm3/g.View SolutionQuestion 212
In the vicinity of the triple point the saturated vapour pressure p of carbon dioxide depends on temperature T as log p=1−b/T, where a and b are constants. If p is expressed in atomspheres, then for the sublimation processa=9.05 and b=1.80kK, and for the vaporization process a=6.78 and b=1.31kK. Find :
(a) temperature and pressure at the triple point ,
(b) the values of the specific latent heats of sublimation, vaporization, and melting in the vicinity of the triple point.View SolutionQuestion 216
A chunk of ice of mass m1=100g at a temperature t1=100g was at a temperature t2. Assuming the heat capacity of the calorimeter to be negligible, find the entropy increment of the system by the moment the thermal equilibrium is reached. Consider two cases :
(a) t2=60∘C ,
(b) t2=94∘C.View SolutionQuestion 217
Molten lead of mass m=5.0g at a temperature t2=327∘C (the melting temperature of lead) was poured into a calorimeter packed with a large amount of ice at a temperature t1=0∘C. Find the entropy increment of the system lead-ice by the moment the thermal equilibrium is reached. The specific latent heat of melting of lead is equal to q=22.5J/g and its specific heat capacity is equal to c=0.125J/(g.K).View SolutionQuestion 218
A water vapour filling the space under the piston of a cylinder is compressed (or expanded) so that it remaind saturated all the time, being just on the verge of condensation. Find the molar heat capacity C of the vapour in this process as a function of temperature T, assuming the vapour to be an ideal gas and neglecting the specific volume of water in comparion with that of vapour. Calculate C at a temperature t=100∘C.View SolutionQuestion 219
One mole of water being in equilibrium with a negligible amount of its saturated vapour at a temperature T1 was completely converted into saturated vapour at a temperature T2. Find the entropy increment of the system. The vapour is assumed to be an ideal gas, the specific volume of the liquid is negligible on comparsion with that of the vapour.View SolutionQuestion 227
Oxygen is enclosed at the temperature 0∘C in a vessel with the characteristic dimension l=10mm (this is the linear dimension determining the character of a physical process in question). Find :
(a) the gas pressure below which the mean free path of the molecules λ>l ,
(b) the corresponding molecular concentration and the mean distanace between the molecules.View SolutionQuestion 234
An ideal gas of molar mass M is enclosed in a vessel of volume of V whose thin walls are kept at a constant temperature T. At a moment t=0 a small hole of area S is opened, and the gas starts escaping into vacuum. Find the gas concentration n as a function of time t if at the initial moment n(0)=n0.View SolutionQuestion 235
A vessel filled with gas is divided into two equal parts 1 and 2 by a thin heat-insulating partition with two holes. One hole has a small diameter, and the other has a very large diameter (in comparsion with the mean free path of molecules). In part 2 the gas is kept at a temperature η times higher than that of part 1 How will the concentration of molecules in part 2 change and how many times after the large hole is closed ?View SolutionQuestion 242
Under standard conditions helium fills up the space between two long coaxial cylinders. The mean radius of the cylinders is equal to R, the gap between them is equal to ΔR, with ΔR<<R. The outer cylinder rotates with a fairly low angular velocity ω about the stationary inner cylinder. Down to what magnitude should the helium pressure be lowered (keeping the temperature constant) to decrease the sought moment of friction forces n=10 times if ΔR=6mm ?View SolutionQuestion 243
A gas fills up the space between two long coaxial cylinders of radii R1 and R2, with R1<R2. The outer cylinder rotates with a fairly low angular velocity ω about the stationary inner cylinder. The moment of friction forces acting on a unit length of the inner cylinder is equal to N1. Find the viscosity coefficient η of the gas taking into account that the friction force acting on a unit area of the cylindrical surface of radius r is determined by the formule σ=ηr(∂ω/∂r).View SolutionQuestion 244
Two identical parallel discs have a common axis and are located at a distance h from each other. The radius of each disc is equal to q, with a>>h. One disc is rotated with a low angular velocity ω relative to the other, stationary, disc. Find the moment of friction forces acting on the stationary disc if the viscosity coefficient of the gas between the disc is equal to η.View SolutionQuestion 248
Two rods whose lengths are l1 and l2 and heat conductivity coefficient x1 and x2 are placed end to end. Find the heat conductivity coefficient of a uniform rod of length l1+l2 whose conductivity is the same as that of the system of these two rods. The lateral surfaces of the rods are assumed to be thermally insulated.View SolutionQuestion 249
A rof of length l with thermally insulated lateral surface consists of material whose heat conductivity coefficient varies with temperature as x=α/T, where α is a constant. The ends of the rod are kept at temperatures T1 and T2. Find the function T(x), where x is the distance from the end whose temperature is T1, and the heat flow density.View SolutionQuestion 250
Two chunks of metal with heat capacities C1 and C2, are interconnected by a rod length l and cross-sectional area S and fairly low heat conductivity K. The whole system is thermally insulated from the environment. At a moment t=0 the temperature difference betwene the two chunks of metal equals (ΔT)0. Assuming the heat capacity of the rod to be negligible, find the temperature difference between the chucks as a function of time. View SolutionQuestion 256
A constant electric current flows along a uniform wire with cross-sectional radius R and heat conductivity coefficient x. A unit volume of the wire generates a thermal power ω. Find the temperature distribution across the wire provided the steady-state temperature at the wire surface is equal to T0.View Solution
.
.
.