Complete Solutions to All Questions of chapter CIRCLES of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | CIRCLES |
| Mathematics | All Questions |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
If radii of the two concentric circles are 15cm and 17cm, then the length of each chord of one circle which is tangent to other is: 8cm (b) 16cm (c) 30cm (d) 17cm
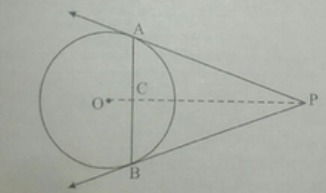
View SolutionIn Figure, if `P R` is tangent to the circle at `P` and `Q` is the centre of the circle, then `/_P O Q=`
View SolutionIf from a point `P ,` tangents `P Qa n dP R` are drawn to the ellipse `(x^2)/2+y^2=1` so that the equation of `Q R` is `x+3y=1,` then find the coordinates of `Pdot`
View SolutionIn Figure, if tangents `PA and P B` are drawn to a circle such that `/_A P B=30^0` and chord `A C` is drawn parallel to the tangent `P B ,` then `/_A B C=` `(a) 60^0` `(b) 90^0` `(c) 30^0` (d) None of these
View SolutionIn two concentric circles, a chord of length 24cm of larger circle becomes a tangent to the smaller circle whose radius is 5cm. Find the radius of the larger circle.
View SolutionIn two concentric circle, prove that a chord of larger circle which is tangent to smaller circle is bisected at the point of contact.
View SolutionFrom an external point `P ,` two tangents `PA` and `PB` are drawn to the circle with centre `O`. Prove that `O P` is the perpendicular bisector of `A B`.
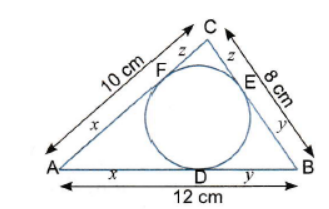
View SolutionA circle is inscribed in a ` A B C` having side `8c m ,10 c ma n d12 c m` as shown in Figure. Find `A D ,B Ea n dC Fdot`
View Solution`A B C D` is a quadrilateral such that `/_D=90^circ` A circle `C(O , r)` touches the sides `A B ,B C ,C D` and `D A` at `P ,Q, R` and `S` respectively. If `B C=38 c m ,C D=25 c m` and `B P=27 c m ,` find `rdot`
View Solution`PA and PB` are tangents from `P` to the circle with centre `Odot` At point `M ,` a tangent is drawn cutting `P A` at `K` and `P B` at `Ndot` Prove that `K N=A K+B Ndot`
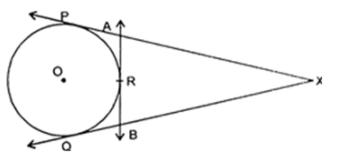
View SolutionIn Figure, `X Pa n dX Q` are tangents from `X` to the circle with centre `OdotR` is a point on the circle. Prove that, `X A+A R=X B+B R`
View SolutionIn figure, sides `Q P` and `R Q` of `P Q R` are produced to point `S` and `T` respectively. If `/_S P R=135^0` and `/_P Q T=110^0,` find `/_P R Qdot` Figure
View SolutionTwo concentric circles are of diameters 30cm and 18cm. Find the length of the chord of the larger circle which touches the smaller circle.
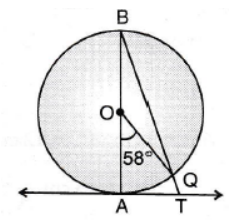
View SolutionIn the given figure, AB is diameter of a circle with centre O and AT is a tangent at `angleAOQ=58^@`, find `angleATQ`.
View SolutionIn Figure, triangle ` A B C` is drawn to circumscribe a circle of radius 4cm such that the segments `B Da n dD C` are of lengths 8cm and 6cm respectively. Find the lengths of sides `A Ba n dA C ,` when area of ` A B C` is `84 c m^2dot`
View SolutionIn Figure, `B C` is a tangent to the circle with centre `OdotO E` bisects `A Pdot` Prove that ` A E O ~ A B Cdot`
View SolutionIn Figure, two tangents `A Ba n dA C` are drawn to a circle with centre `O` such that `/_B A C=120^0dot` Prove that `O A=2A B`
View SolutionIn the given figure, O is the centre of the circle and OLM is perpendicular to AOB. Prove that (i) A, O, P and M are concyclic (ii) `/_OAP =/_OMB` (iii) P, L, O and B are concyclic
View SolutionIn Figure, common tangents P Q and RS to two circle intersect at A. Prove that PQ=RS
View SolutionCircles C(O, r) and C(O', r'), `(r gt r') ` touch internally at P. PQ is a chord of circle C(O, r) which intersects C(O', r') at R. Show that OO'RQ is a trapezium
View SolutionTwo concentric circles of radii ` 3 cm and 5 cm` are given. Then length of chord `B C` which touches the inner circle at `P` is equal to (a) 4 cm (b) 6cm (c) 8 cm (d) 10 cm
View SolutionIn Figure, a circle with centre `O` is inscribed in a quadrilateral ABCD such that, it touches sides BC, AB, AD and C D at points P, Q, R and S respectively. If `A B=29c m ,A D=23 c m ,/_B=90^0` and `D S=5c m ,` then the radius of the circle (in cm) is (a) 11 (b) 18 (c) 6 (d) 15
View SolutionIn Figure, `O` is the centre of the circle and `B C D` is tangent to it at `Cdot` Prove that `/_B A C+/_A C D=90^0` .
View SolutionIn Figure, there are two concentric circles with centre `O` of radii `5 cm and 3 cm` . From an external point `P ,` tangents `PA and PB` are drawn to these circles. If `A P=12 cm ,` find the length of `BPdot`
View Solution. In the given figure, two equal circles, with centres O and O', touch each other at X. OO' produced me the circle with centre O' at A. AC is tangent to the circle with centreO, at the point C. O'D is perpendicular to AC. Find the value of `(DO')/(CO)`.
View SolutionProve that the line segment joining the points of contact of two parallel tangents passes through the centre.
View Solutionabout to only mathematics
View SolutionIn two concentric circles prove that all chords of the outer circle which touch the inner circle are of equal length.
View SolutionIn Figure, `O\ a n d\ O '` are centres of two circles intersecting at `B\ a n d\ C. A C D` is a straight line, find `x`.
View SolutionTwo circles with centres `Aa n dB` of radii `3c ma n d4c m` respectively intersect at two points `Ca n dD` such that `A Ca n dB C` are tangents to the two circles. Find the length of the common chord `C Ddot`
View SolutionIf an isosceles `DeltaABC` in which AB=AC=6cm, is inscribed in a circle of radius 9cm, find the area of the triangle.
View SolutionO is the centre of a circle of radius 5cm. T is a point such that OT=13cm and OT intersects the circle at E. If AB is the tangent to the circle at E, find length of AB.
View SolutionAB is a diameter of a circle with centre O, AH and BK are perpendiculars from A and B to the tangent at a point P on the circle, Prove that AH+BK=AB.

View SolutionA tangent `P Q` at a point `P` of a circle of radius 5 cm meets a line through the centre `O` at a point `Q` so that `O Q=13 c m` . Find the length of `P Q` .
View SolutionA line through the centre `O` of a circle of radius 7 cm cuts the tangent, at a point `P` on the circle, at `Q` such that `P Q=24 c m` . Find `O Q` .
View SolutionFill in the blanks: The common point of a tangent and the circle is called...... A circle may have ..... parallel tangents. A tangent to a circle intersects it in ..... point(s). A line intersecting a circle in two points is called a ........ (v) The angle between tangent at a point on a circle and the radius through the point is .........
View SolutionHow many tangents can a circle have?
View Solution`O` is the centre of a circle of radius 8 cm. The tangent at a point `A` on the circle cuts a line through `O` at `B` such that `A B=15 c m` . Find `O B` .
View SolutionIf the tangent at a point `P` to a circle with centre `O` cuts a line through `O` at `Q` such that `P Q=24 c m` and `O Q=25 c m` . Find the radius of the circle.
View SolutionA point `P` is 13cm from the centre of the circle. The length of the tangent drawn from `P` to the circle is 12 cm. Find the radius of the circle.
View SolutionFind the length of the tangent drawn from a point whose distance from the centre of a circle is 25 cm. Given that the radius of the circle is 7 cm.
View SolutionA circle is touching the side `B C` of ` A B C` at `P` and touching `A B` and `A C` produced at `Q` and `R` respectively. Prove that `A Q=1/2(P e r i m e t e r\ of\ A B C)` .
View SolutionIn Figure, the incircle of ` A B C` touches the sides `B C ,\ C A` and `A B\ a t\ D ,\ E` and `F` respectively. Show that `A F+B D+C E=A E+B F+C D=1/2(P e r i m e t e r\ of\ A B C)`.
View SolutionIn Fig. 10.20, the sides `A B ,\ B C` and `C A` of triangle `A B C` touch a circle with centre `O` and radius `r` at `P ,\ Q` and `R` respectively. (FIGURE) Prove that: 1) AB + CQ = AC + BQ
View SolutionIn Figure, two circles touch each other at the point `C` . Prove that the common tangent to the circles at `C` , bisects the common tangent at `P` and `Q` .
View SolutionA circle touches all the four sides of a quadrilateral `A B C D` . Prove that: `A B+C D=B C+D A` .
View SolutionIf all the side of a parallelogram touch a circle, show that the parallelogram is a rhombus. OR Prove that a parallelogram circumscribing a circle is a rhombus.
View SolutionThe radius of the incircle of a triangle is 4 cm and the segments into which one side is divided by the point of contact are 6 cm and 8 cm. Determine the other two sides of the triangle.
View SolutionProve that the tangents at the extremities of any chord make equal angles with the chord.
View SolutionTwo tangents `T P` and `T Q` are drawn to a circle with centre `O` from an external point `T` . Prove that `/_P T Q=2/_O P Q` .
View Solution`P Q` is a chord of length 8 cm of a circle of radius 5 cm. The tangents at `P` and `Q` intersect at a point `T` . Find the length `T P` .
View SolutionIn Figure, `n` and `m` are two parallel tangents at `A` and `B` . The tangent at `C` makes an intercept `D E` between `n` and `m` . Prove that `/_D F E=90^@` .
View SolutionProve that the angle between two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segments joining the points of contact at the centre.
View SolutionShow that tangent lines at the end points of a diameter of a circle are parallel.
View SolutionTwo concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
View SolutionA circle touches the sides of a quadrilateral `A B C D` at `P ,\ Q ,\ R ,\ S` respectively. Show that the angles subtended at the centre by a pair of opposite sides are supplementary.
View SolutionFind the locus of centres of circles which touch two intersecting lines.
View SolutionFind the locus of centres of circles which touch two intersecting lines.
View SolutionIf `P T` is a tangent at `T` to a circle whose centre is `O` and `O P=17 c m` , `O T=8c m` , Find the length of the tangent segment `P T` .
View SolutionFind the length of a tangent drawn to a circle with radius 5 cm, from a point 13 cm from the centre of the circle.
View SolutionA point is 26 cm away from the centre `O` of a circle and the length `P T` of the tangent drawn from `P` to the circle is 10 cm. Find the radius of the circle.
View SolutionIf from any point on the common chord of two intersecting circles, tangents be drawn to the circles, prove that they are equal.
View SolutionIf the sides of a quadrilateral touch a circle, prove that the sum of a pair of opposite sides is equal to the sum of the other pair.
View SolutionIf `A B ,\ A C ,\ P Q` are tangents in Fig. 10.51 and `A B=5c m` , find the perimeter of ` A P Q` . (FIGURE)
View SolutionProve that the intercept of a tangent between two parallel tangents to a circle subtends a right angle at the centre.
View SolutionIn Fig. `P Q` is tangent at a point `R` of the circle with centre `O` . If `/_T R Q=30^o` , find `/_P R S` . (FIGURE)
View SolutionIf `P A` and `P B` are tangents from an outside point `P` such that `P A=10 c m` and `/_A P B=60^o` . Find the length of chord `A B` .
View SolutionFrom an external point `P` , tangents `P A` and `P B` drawn to a circle with centre `O` . If `C D` is the tangent to the circle at a point `E` and `P A=14 c m` , find the perimeter of ` P C D` .
View SolutionIn Fig. 10.53, `A B C` is a right triangle right-angled at `B` such that `B C=6c m` and `A B=8c m` . Find the radius of its incircle. (FIGURE)
View SolutionFrom a point `P` , two tangents `P A` and `P B` are drawn to a circle with centre `O` . If `O P=` diameter of the circle, show that `/_\ A P B` is equilateral.
View SolutionTwo tangent segments `P A` and `P B` are drawn to a circle with centre `O` such that `/_A P B=120^circ` . Prove that `O P=2\ A P` .
View SolutionIf ` A B C` is isosceles with `A B=A C` and `C(O ,\ r)` is the incircle of the ` A B C` touching `B C` at `L` , prove that `L` bisects `B C` .
View SolutionIn Fig. 10.54, a circle touches all the four sides of a quadrilateral `A B C D` with `A B=6c m` , `B C=7c m` and `C D=4c m` . Find `A D` . (FIGURE)
View SolutionProve that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
View SolutionTwo circles touch externally at a point `P`. From a external point `T` on the tangent at `P`, tangents `T Q` and `T R` are drawn to the circles with points of contact `Q` and `R` respectively. Prove that `T Q = T R`.
View SolutionIn Fig. 10.57, a circle is inscribed in a quadrilateral `A B C D` in which `/_B=90o` . If `A D=23 c m` , `A B=29 c m` and `D S=5c m` , find the radius `r` of the circle. (FIGURE)
View Solution`A B` is a chord of length 16cm of a circle of radius 10cm. The tangents at `A` and `B` intersect at a point `P` . Find the length of `P A` .
View SolutionIn Figure, `P A` and `P B` are tangents from an external point `P` to a circle with centre `O` . `L N` touches the circle at `M` . Prove that `P L+L M=P N+M N` .
View SolutionIn Figure, `B D C` is a tangent to the given circle at point `D` such that `B D=30 c m` and `C D=7c m` . The other tangents `B E` and `C F` are drawn respectively from `B` and `C` to the circle and meet when produced at `A` making `B A C` a right angle triangle. Calculate (i) `A F` (ii) radius of the circle.
View SolutionIn Fig. 10.62, `P O_|_Q O` . The tangents to the circle at `P` and `Q` intersect at a point `T` . Prove that `P Q` and `O T` are right bisectors of each other. (FIGURE)
View SolutionThe lengths of three consecutive sides of a quadrilateral circumscribing a circle are 4 cm, 5cm, and 7cm respectively. Determine the length of the fourth side.
View SolutionIn Fig. 10.67, `O Q : P Q=3:4` and perimeter of ` P O Q=60 c m` . Determine `P Q ,\ Q R` and `O P` . (FIGURE)
View SolutionIn Fig. 10.72, `P A` and `P B` are tangents to the circle drawn from an external point `P` . `C D` is a third tangent touching the circle at `Q` . If `P B=10 c m` and `C Q=2c m` , what is the length `P C` ? (FIGURE)
View SolutionWhat is the distance between two parallel tangents of a circle of radius 4 cm?
View SolutionThe length of a tangent from a point A at distance 5 cm from the centre of the circle is 4cm. Find the radius of the circle.
View SolutionTwo tangents `T P` and `T Q` are drawn from an external point `T` to a circle with centre `O` as shown in Fig. 10.73. If they are inclined to each other at an angle of `100o` , then what is the value of `/_P O Q` ?
View SolutionWhat is the distance between two parallel tangents to a circle of radius 5 cm?
View SolutionIn Q. No. 1, if `P B=10 c m` , what is the perimeter of ` P C D` ?
View SolutionIn Fig. 10.74, `C P` and `C Q` are tangents to a circle with centre `O` . `A R B` is another tangent touching the circle at `R` . If `C P=11 c m` and `B C=7c m` , then find the length of `B R` . (FIGURE)
View SolutionIn figure ΔABC is circumscribing a circle. Find the length of BC
View SolutionIn Fig. 10.76, `C P` and `C Q` are tangents from an external point `C` to a circle with centre `O` . `A B` is another tangent which touches the circle at `R` . If `C P=11 c m` and `B R=4c m` , find the length of `B C` . (FIGURE)
View SolutionTwo concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
View SolutionIn Figure, `P A` and `P B` are tangents to the circle with centre `O` such that `/_A P B=50^@` . Write the measure of `/_O A B` .
View SolutionA tangent `P Q` at a point `P` of a circle of radius 5 cm meets a line through the centre `O` at a point `Q` such that `O Q=12 c m` . Length `P Q` is
View SolutionFrom a point `Q` , the length of the tangent to a circle is 24cm and the distance of `Q` from the centre is 25cm. The radius of the circle is
View SolutionThe length of the tangent from a point `A` to a circle, of radius 3cm, is 4cm. The distance of `A` from the centre of the circle is
View SolutionIf tangents `P A` and `P B` from a point `P` to a circle with centre `O` are inclined to each other at an angle of `80^o` then `/_P O A` is equal to :
View SolutionIn figure, sides `Q P` and `R Q` of `P Q R` are produced to point `S` and `T` respectively. If `/_S P R=135^0` and `/_P Q T=110^0,` find `/_P R Qdot` Figure
View Solution`P Q` is a tangent to a circle with centre `O` at the point `P` . If `/_\ O P Q` is an isosceles triangle, then `/_O Q P` is equal to :
View SolutionTwo equal circles touch each other externally at `C` and `A B` is a common tangent to the circles. Then, `/_A C B=` `60o` (b) `45o` (c) `30o` (d) `90o`
View Solution
All Questions questions and complete solutions for chapter CIRCLES of RD SHARMA MATHS (ENGLISH) of Class 10