PHYSICS from ARIHANT PHYSICS Chapter 12 ROTATIONAL MOTION for Class 11
| Class 11 | PHYSICS |
| Chapter | ROTATIONAL MOTION |
| ARIHANT PHYSICS | PHYSICS |
| Medium | English |
| Academic Year | 2023-2024 |
Question 1
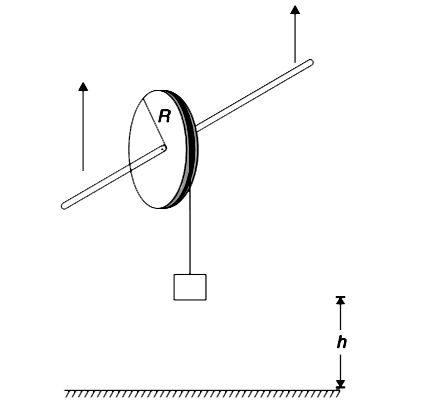
The pulley of radius R can rotate freely about its axle as shown in the figure. A thread is tightly wrapped around the pulley and its free end carries a block of mass m. When the block is at a height h above the ground the system is released (i.e., the pulley is made free to rotate & the block is allowed to fall) and at the same instant the axle is moved up keeping it horizontal all the time. When the block hits the floor the axle has gone up by a distance 2h. Find the angle by which the pulley must have rotated by this time.
 View Solution
View SolutionQuestion 7
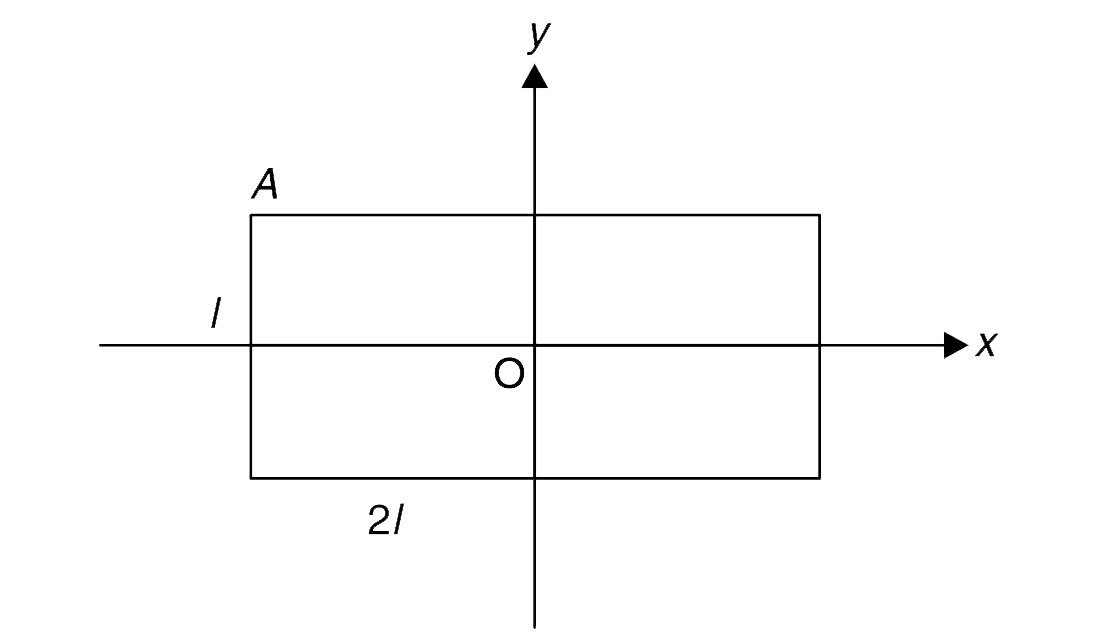
A uniform rectangular plate has side length l and 2l. The plate is in x−y plane with its centre at origin and sides parallel to x and y axes. The moment of inertia of the plate about an axis passing through a vertex (say A) perpendicular to the plane of the figure is I0. Now the axis is shifted parallel to itself so that moment of inertia about it still remains I0. Write the locus of point of intersection of the axis with xy plane
 View Solution
View SolutionQuestion 9
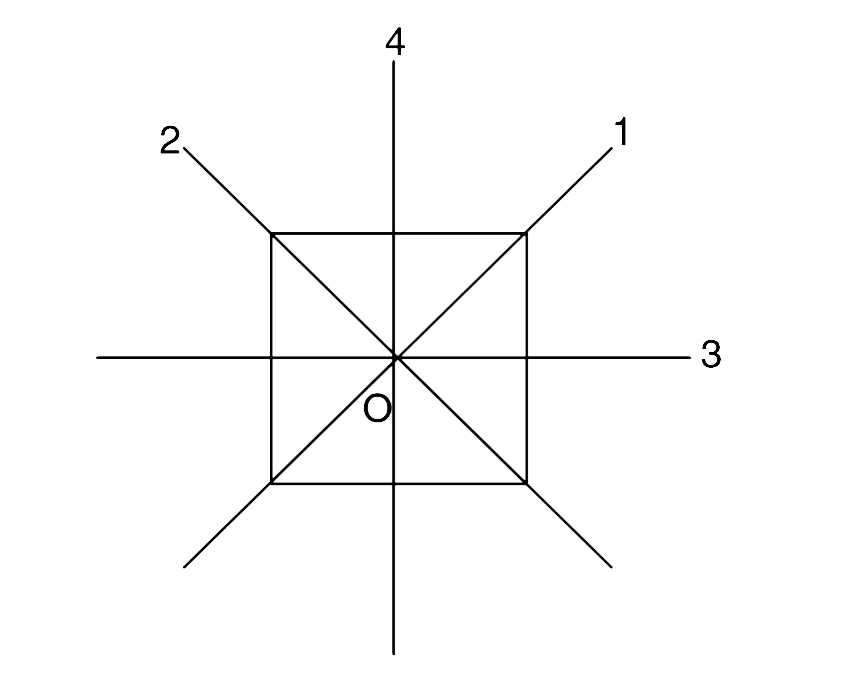
Consider a uniform square plate shown in the figure. I1,I2,I3 and I4 are moment of inertia of the plate about the axes 1, 2, 3 and 4 respectively. Axes 1 and 2 are diagonals and 3 and 4 are lines passing through centre parallel to sides of the square. The moment of inertia of the plate about an axis passing through centre and perpendicular to the plane of the figure is equal to which of the followings.
(a) I3+I4
(b) I1+I3
(c) I2+I3
(d) 12(I1+I2+I3+I4)
 View Solution
View SolutionQuestion 11
(i) Consider an infinitesimally thin triangular strip having mass M and length L. Find the moment of inertia of the strip about on axis passing through its tip and perpendicular to the plane. Compare the result with moment of inertia of a uniform disc of mass M and radius L about an axis passing through its centre and perpendicular to the plane the disc. Why the two expressions are same?

(ii) A circular fan made of paper is in shape of a disc of radius R. The fan can be folded (various stages shown in figure (a) through (f)) to the shape of a thin stick. The moment of inertia of the circular fan about an axis passing through centre O and perpendicular to the plane of the figure is I0=12MR2 where M= mass of the fan.

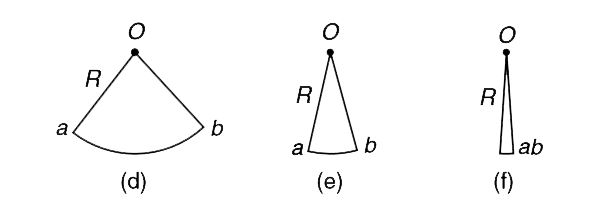
(a) How does the moment of inertia (I), about an axis perpendicular to the plane of the figure passing through O, change as the fan is folded through stage a to b to c to d to e?
(b) When the fan is completely folded in the shape of a stick (fig. (f)), write its moment of inertia about the above mentioned axis.
Note : Moment of inertia of a uniform rod about an axis through its end and perpendicular to it is ML23View SolutionQuestion 12
A uniform rectangular plate has moment of inertia about its longer side, equal to I. The moment of inertia of the plate about an axis in its plane, passing through the centre and parallel to the shorter sides is also equal to I. Find its moment of inertia about an axis passing through its centre and perpendicular to its plane. View SolutionQuestion 13
A uniform rectangular plate has been bent as shown in the figure. The two angled parts of the plate are of identical size. The moment of inertia of the bent plate about axis xx is I. Find its moment of inertia about an axis parallel to xx and passing through the centre of mass of the plate.
 View Solution
View SolutionQuestion 14
Three identical rings each of mass M and radius R are welded together with their planes mutually perpendicular to each other. Ring A is vertical and B is also vertical in a plane perpendicular to A. Ring C is in horizontal plane. Find moment of Inertia of this system about a horizontal axis perpendicular to the plane of the figure passing through point P (top point of ring A)
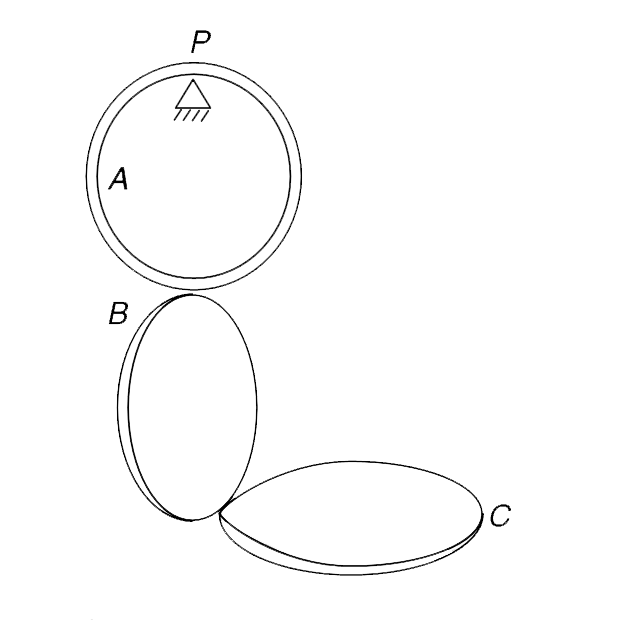 View Solution
View SolutionQuestion 19
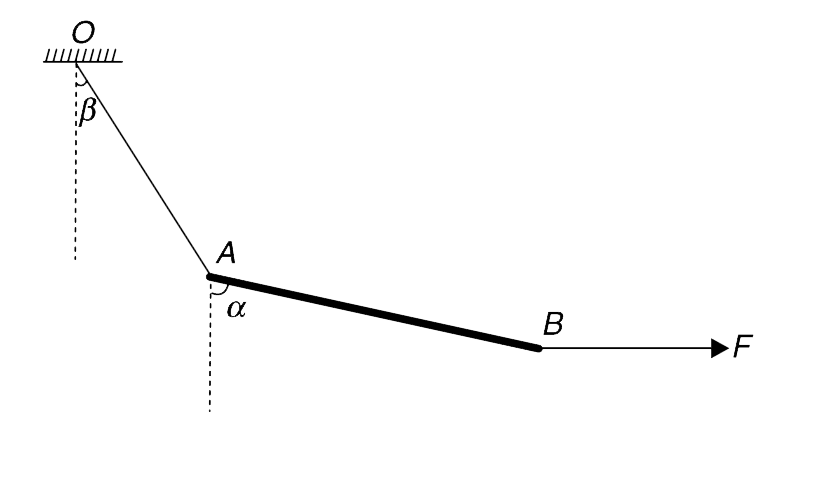
A uniform wire has been bent in shape of a semi circle. The semicircle is suspended about a horizontal axis passing through one of its ends, so that the semicircular wire can swing in vertical plane. Find the angle α that the diameter of the semicircle makes with vertical in equilibrium.
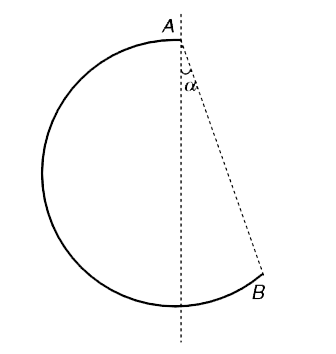 View Solution
View SolutionQuestion 20
A uniform cylindrical body of radius r has a conical nose. The length of the cylindrical and conical parts are 4r and 3r respectively. Mass of the conical part is M. The body rests on a horizontal surface as shown. A ring of radius r2 is to be tightly fitted on the nose of the body. What is maximum permissible mass of the ring so that the body does not topple?
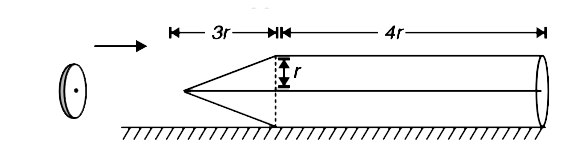 View Solution
View SolutionQuestion 21
There is a step of height h on an incline plane. The step prevents a ball of radius R from rolling down.
(a) If the inclination (θ) of the incline is increased gradually, at what value of θ the ball will just manage to climb the step?

(b) Does the gravitational potential energy of the ball increases or decreases as it climbs the step ?View SolutionQuestion 22
The centre of mass of an inhomogeneous sphere is at a distance of 0.3 R from its geometrical centre. R is the radius of the sphere. Find the maximum inclination (θ) of an incline plane on which this sphere can be placed in equilibrium. Assume that friction is large enough to prevent slipping. View SolutionQuestion 23
Rectangular block B, having height h and width d has been placed on another block A as shown in the figure. Both blocks have equal mass and there is no friction between A and the horizontal surface. A horizontal time dependent force F=kt is applied on the block A. At what time will block B topple? Assume that friction between the two blocks is large enough to prevent B from slipping.
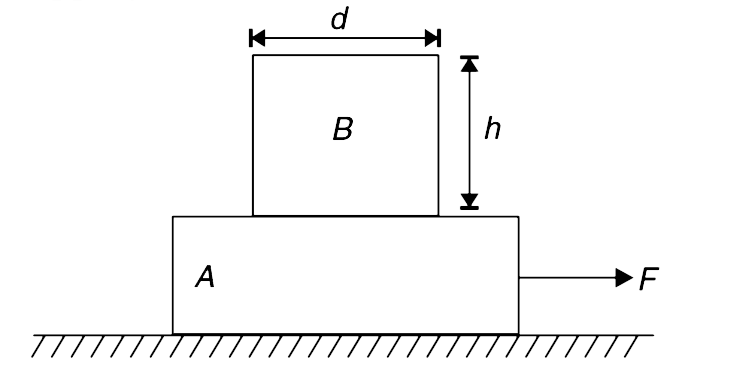 View Solution
View SolutionQuestion 25
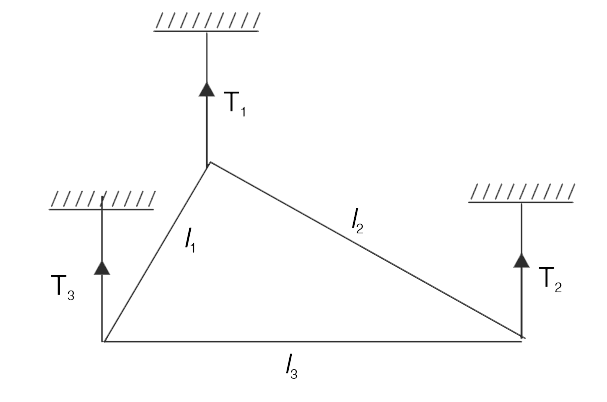
A hollow cylindrical pipe of mass M and radius R has a thin rod of mass m welded inside it, along its length. A light thread is tightly wound on the surface of the pipe. A mass m0 is attached to the end of the thread as shown in figure. The system stays in equilibrium when the cylinder is placed such that α=30∘ The pulley shown in figure is a disc of mass M2
(a) Find the direction and magnitude of friction force acting on the cylinder.
(b) Express mass of the rod ‘m’ in terms of m0
 View Solution
View SolutionQuestion 26
A sphere of radius R is supported by a rope attached to the wall. The rope makes an angle θ=45∘ with respect to the wall. The point where the rope is attached to the wall is at a distance of 3R2 from the point where the sphere touches the wall. Find the minimum coefficient of friction (μ) between the wall and the sphere for this equilibrium to be possible.
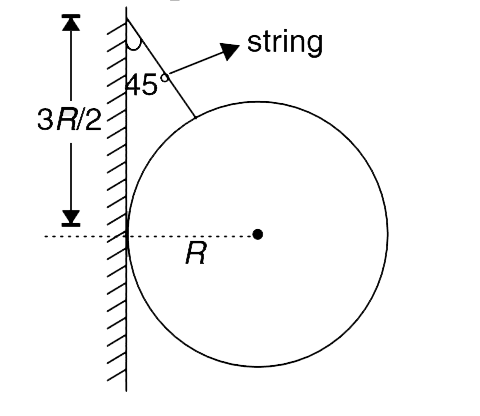 View Solution
View SolutionQuestion 27
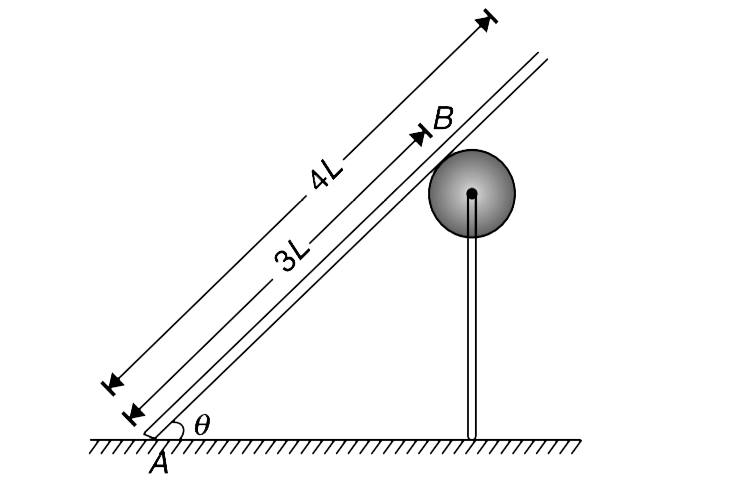
A uniform rod has mass M and length 4L. It rests in equilibrium with one end on a rough horizontal surface at A. At point B, at a distance 3L from A, it is supported by a fixed smooth roller. The rod just remains in equilibrium when θ=30∘
(a) Find the normal force applied by the horizontal surface on the rod at point A.
(b) Find the coefficient of friction between the rod and the surface.
 View Solution
View SolutionQuestion 28
A wheel is mounted on frictionless central pivot and it can rotate freely in the vertical plane. There is a horizontal light rod fixed to the wheel below the pivot. There is a small sleeve of mass m which can slide along the rod without friction. The sleeve is connected to a light spring. The other end of the spring is fixed to the rim as shown. The sleeve is at the centre of the rod and the spring is relaxed. Now the wheel is held at rest and the sleeve is moved towards left so as to compress the sprig by some distance. The sleeve and the wheel are released simultaneously from this position.
(a) Is it possible that the wheel does not rotate as the sleeve perform SHM on the rod ?
(b) Find the value of spring constant k for situation described in (a) to be possible. The distance of rod from centre of the wheel is d.
 View Solution
View SolutionQuestion 29
A string is wrapped around a cylinder of mass M and radius R. The string is pulled vertically upward to prevent the centre of mass from falling as the string unwinds. Assume that the cylinder remains horizontal throughout and the thread does not slip. Find the length of the string unwound when the cylinder has reached an angular speed ω.
 View Solution
View SolutionQuestion 30
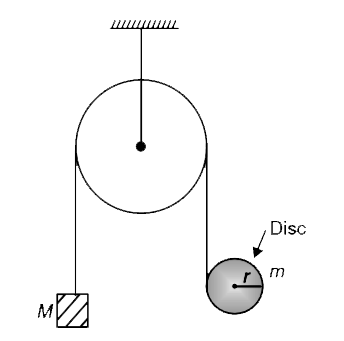
A mass less string is wrapped around a uniform disc of mass m and radius r. The string passes over a mass less pulley and is tied to a block of mass M at its other end (see figure). The system is released from rest. Assume that the string does not slip with respect to the disc.
(a) Find the acceleration of the block for the case M=m
(b) Find Mm for which the block can accelerate upwards.
 View Solution
View SolutionQuestion 31
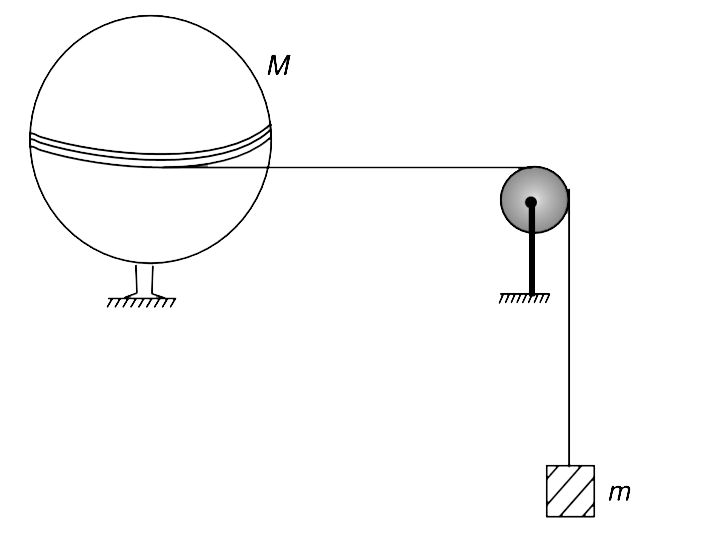
A solid uniform sphere of mass M and radius R can rotate about a fixed vertical axis. There is no frictional torque acting at the axis of rotation. A light string is wrapped around the equator of the sphere. The string has exactly 6 turns on the sphere. The string passes over a light pulley and carries a small mass m at its end (see figure). The string between the sphere and the pulley is always horizontal. The system is released from rest and the small mass falls down vertically. The string does not slip on the sphere till 5 turns get unwound. As soon as 5th turn gets unwound completely, the friction between the sphere and the string vanishes all of a sudden.
(a) Find the angular speed of the sphere as the string leaves it.
(b) Find the change in acceleration of the small mass m after 5 turns get unwound from the sphere.
 View Solution
View SolutionQuestion 32
A disc of mass m and radius R lies flat on a smooth horizontal table. A mass less string runs halfway around it as shown in figure. One end of the string is attached to a small body of mass m and the other end is being pulled with a force F. The circumference of the disc is sufficiently rough so that the string does not slip over it. Find acceleration of the small body.
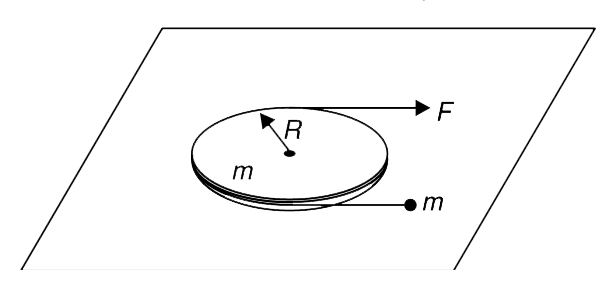 View Solution
View SolutionQuestion 33
A uniform quarter circular thin rod of mass M and radius R is pivoted at a point B on the floor. It can rotate freely in the vertical plane about B. It is supported by a smooth vertical wall at its other free end A so that it remains at rest. Find the reaction force of wall on the rod.
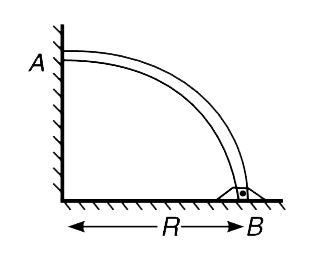 View Solution
View SolutionQuestion 35
A solid sphere of mass M and radius R is covered with a thin shell of mass M. There is no friction between the inner wall of the shell and the sphere. The ball is released from rest, and then it rolls without slipping down an incline that is inclined at an angle θ to the horizontal. Find the acceleration of the ball. View SolutionQuestion 36
A homogeneous solid sphere of radius R is resting on a horizontal surface. It is set in motion by a horizontal impulse imparted to it at a height h above the centre. If h is greater than h0, the velocity of the sphere increases in the direction of its motion after the start. If h<h0 the velocity decreases after the start. Find h0
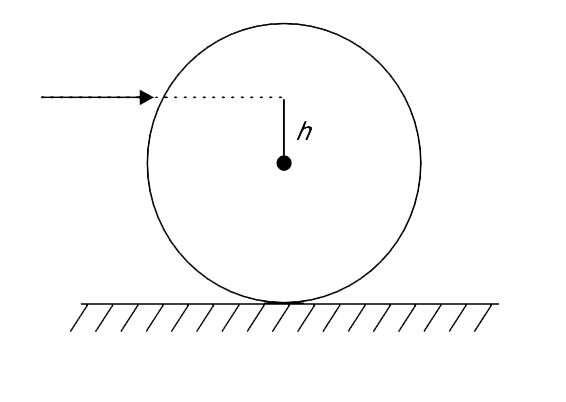 View Solution
View SolutionQuestion 37
A boy pushes a cylinder of mass M with the help of a plank of mass m as shown in figure. There is no slipping at any contact. The horizontal component of the force applied by the boy on the plank is F. Find
(a) The acceleration of the centre of the cylinder
(b) The friction force between the plank and the cylinder
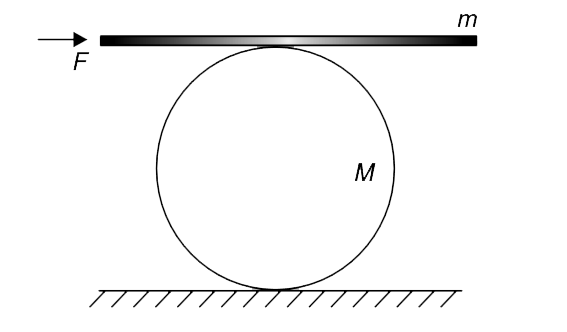 View Solution
View SolutionQuestion 38
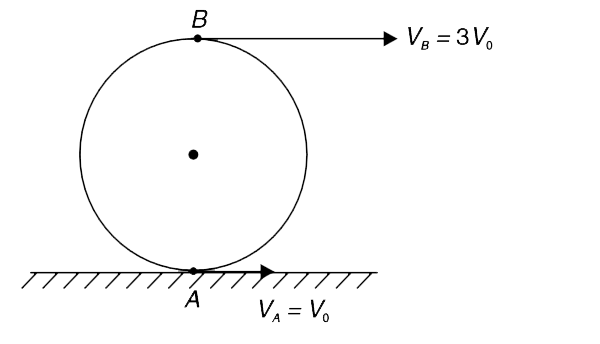
(i) A solid sphere of radius R is released on a rough horizontal surface with its top point having thrice the velocity of its bottom point A (VA=V0) as shown in figure. Calculate the linear velocity of the centre of the sphere when it starts pure rolling.
(ii) Solid sphere of radius R is placed on a rough horizontal surface with its centre having velocity V0 towards right and its angular velocity being ω0 (in anticlockwise sense). Find the required relationship between V0 and ω0 so that -
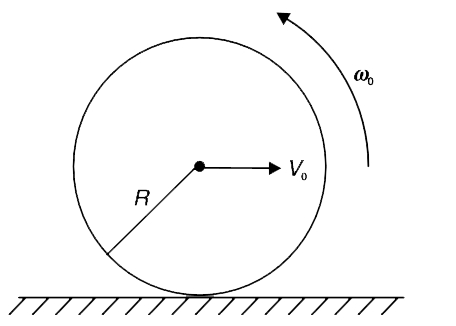
(a) the slipping ceases before the sphere loses all its linear momentum.
(b) the sphere comes to a permanent rest after some time.
(c) the velocity of centre becomes zero before the spinning ceases.View SolutionQuestion 39
A thin pencil of mass M and length L is being moved in a plane so that its centre (i.e. centre of mass) goes in a circular path of radius R at a constant angular speed ω. However, the orientation of the pencil does not change in space. Its tip (A) always remains above the other end (B) in the figure shown
(a) Write the kinetic energy of the pencil.
(b) Find the magnitude of net force acting on the pencil.
 View Solution
View SolutionQuestion 40
In figure (a) there is a uniform cylinder of mass M and radius R. Length of the cylinder is L=√3R. The cylinder is rolling without sliding on a horizontal surface with its centre moving at speed V. In figure (b) the same cylinder is moving on a horizontal surface with its centre moving at speed V and the cylinder rotating about a vertical axis passing through its centre. [Place your pencil on the table and give a sharp blow at its end. Look at the motion of the pencil. This is how the cylinder is moving]. The angular speed is ω=VR. Write the kinetic energy of the cylinder in two cases. In which case, the kinetic energy would have been higher if length of the cylinder were doubled (=2√3R).
(a) View Solution
View SolutionQuestion 41
There is a fixed hollow cylinder having smooth inner surface. Radius of the cylinder is R=4m. A uniform rod of M=4kg and length L=4m is released from vertical position inside the cylinder as shown in the figure. Convince yourself that the rod will perform pure rotation about the axis of the cylinder passing through O. Fid the angular speed of the rod when its becomes horizontal.
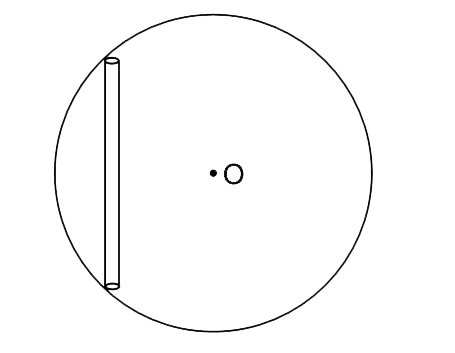 View Solution
View SolutionQuestion 42
A disc shaped body has two tight windings of light threads - one on the inner rim of radius R=1m and the other on outer rim of radius 2R (see figure). It is kept on a horizontal surface and the ends of the two threads are pulled horizontally in opposite directions with force of equal magnitude F=20N. Mass of the body and its moment of inertia about an axis through centre O and perpendicular to the plane of the figure are M=4kg and I=8kg−m2 respectively. Find the kinetic energy of the body 2 seconds after the forces begin to act, if
(i) the surface is smooth,
(ii) the surface is rough enough to ensure rolling without sliding.
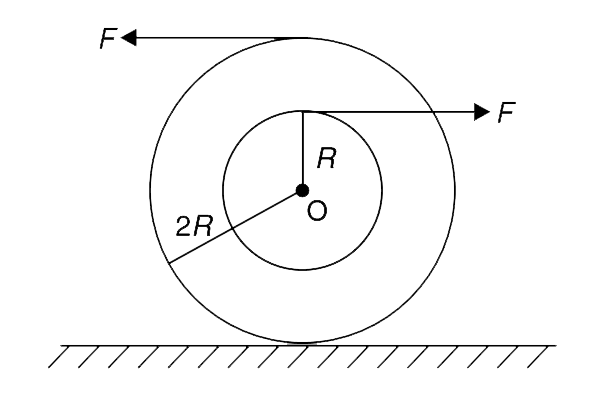 View Solution
View SolutionQuestion 43
A uniform square plate has mass M and side length a. It is made to oscillate in vertical plane in two different ways shown in figure (A) and (B). In figure (A), the plate is hinged at its upper corners with the help of two mass less rigid rods each of length a. The rods can rotate freely about both ends.
(a)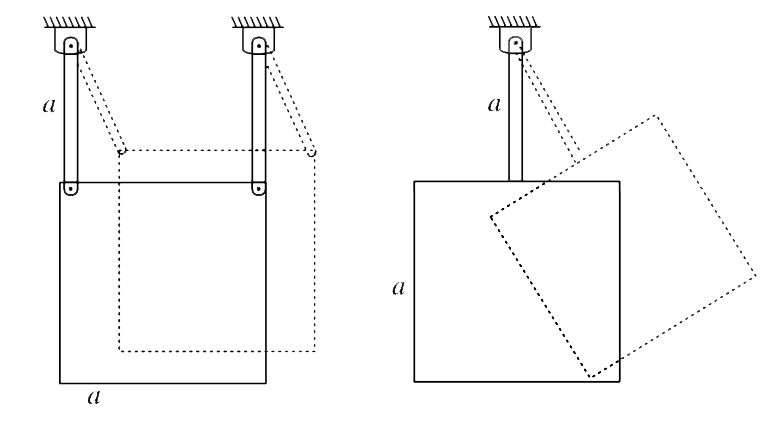
(b)
In figure (B) the plate is rigidly connected at the centre of its top edge to a mass less rod of length a. The rod can rotate about its upper end only. In both cases the plate is pushed from its equilibrium position so that centre of mass of the plate acquires a speed V. In which case will the centre of mass of the plate rise to a greater height. There is no friction. View SolutionQuestion 44
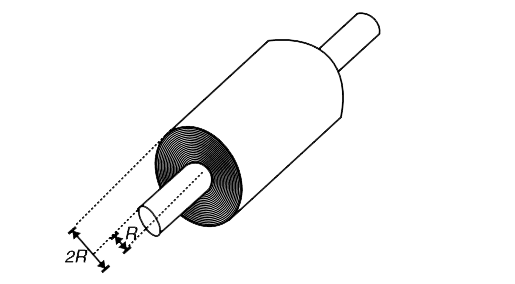
A thin carpet of mass 2m is rolled over a hollow cylinder of mass m. The cylinder wall is thin and radius of the cylinder is R. The carpet rolled over it has outer radius 2R (see figure). This roll is placed on a rough horizontal surface and given gentle push so that the carpet begins to roll and unwind. Friction is large enough to prevent any slipping of the carpet on the floor. Also assume that the carpet does not slip on the surface of the cylinder. The entire carpet is laid out on the floor and the hollow cylinder rolls out with speed V. Find V.
 View Solution
View SolutionQuestion 46
The propeller of a small airplane is mounted in the front. The propeller rotates clockwise if seen from behind by the pilot. The plane is flying horizontally and the pilot suddenly turns it to the right. Will the body of the plane have a tendency to get inclined to the horizontal? If yes, does the nose of the plane veer upward or downward? Why? View SolutionQuestion 47
A massive star is spinning about its diameter with an angular speed ω0=π1000 rad/day. After its fuel is exhausted, the star collapses under its own gravity to form a neutron star. Assume that the volume of the star decreases to 10−12 times the original volume and its shape remains spherical. Assuming that density of the star is uniform, find the angular speed of the neutron star.View SolutionQuestion 48
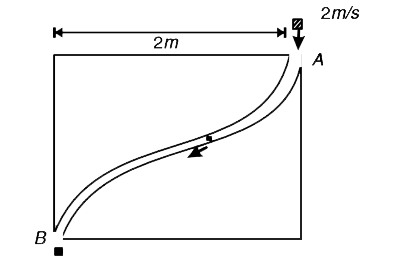
A square plate of side length 2m has a groove made in the shape of two quarter circles joining at the centre of the plate. The plate is free to rotate about vertical axis passing through its centre. The moment of inertia of the plate about this axis is 4kg−m2. A small block of mass 1 kg enters the groove at end A travelling with a velocity of 2/s parallel to the side of the square plate. The block move along the frictionless groove of the horizontal plate and comes out at the other end B with speed V. Find V assuming that width of the groove is negligible.
 View Solution
View SolutionQuestion 49
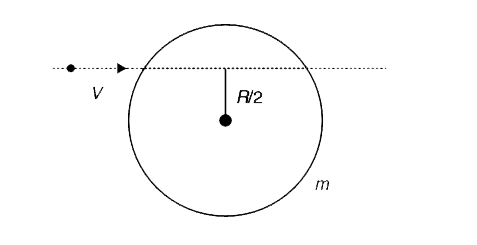
A disc of mass m and radius R lies flat on a smooth horizontal table. A particle of mass m, moving horizontally along the table, strikes the disc with velocity V while moving along a line at a distance R2 from the centre. Find the angular velocity acquired by the disc if the particle comes to rest after the impact.
 View Solution
View SolutionQuestion 50
A disc of mass M and radius R is rotating with angular velocity ω0 about a vertical axis passing through its centre (O). A man of mass M2 and height R2 is standing on the periphery. The man gradually lies down on the disc such that his head is at a distance R2 from the centre and his feet touching the edge of the disc. For simplicity assume that the man can be modelled as a thin rod of length R2. Calculate the angular speed (ω) of the platform after the man lies down.
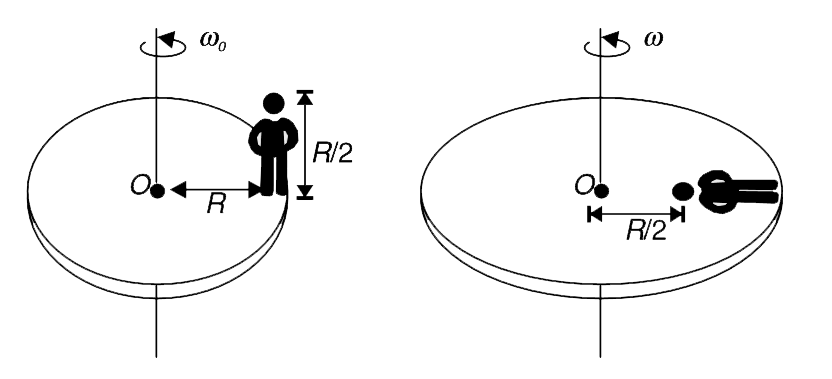 View Solution
View SolutionQuestion 51
A uniform block of mass M and dimensions as shown in the figure is placed on a rough horizontal surface and given a velocity V0 to the right. A is a point on the surface to the left of the block.
(a) Write the angular momentum of the block about point A just after it begins to move
(b) Due to friction the block stops. What happened to its angular momentum about point A? Which torque is responsible for change in angular momentum of the block?
 View Solution
View SolutionQuestion 52
ABCFED is a uniform plate (shown in figure). ABC and DEF are circular arcs with common centre at O and having radii a and 2a respectively. This plate is lying on a smooth horizontal table. A particle of mass half the mass of the plate strikes the plate at point A while travelling horizontally along the x direction with velocity u. The particle hits the plate and rebounds along negative x with velocity u2 . Find the velocity of point D of the plate immediately after the impact. [Take 289π≅1 ]
 View Solution
View SolutionQuestion 53
A uniform rod of mass m and length L is fixed to an axis, making an angle θ with it as shown in the figure. The rod is rotated about this axis so that the free end of the rod moves with a uniform speed ‘v’. Find the angular momentum of the rod about the axis. Is the angular momentum of the rod about point A constant?
 View Solution
View SolutionQuestion 54
A mass m in attached to a mass less string and swings in a horizontal circle, forming a conical pendulum, as shown in the figure. The other end of the string passes through a hole in the table and is dragged slowly so as to reduce the length l. The string is slowly drawn up so that the depth h shown in the figure becomes half. By what factor does the radius (r) of the circular path of the mass m change?
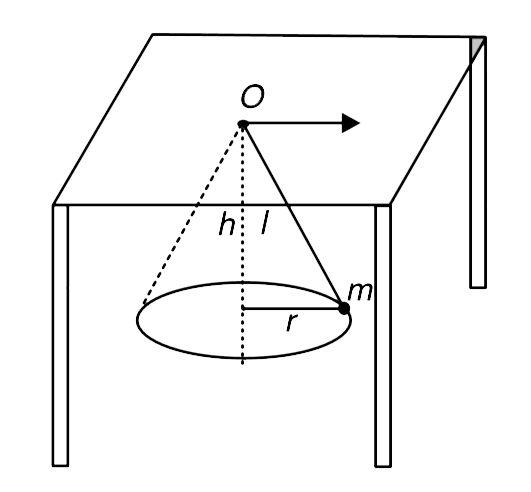 View Solution
View SolutionQuestion 55
A flat rigid body is moving in x–y plane on a table. The plane of the body lies in the x–y plane. At an instant it was found that some of the velocity components of its three particles A, B and C were VAx=4m/s,VBx=3m/s and Vcy=−2m/s, respectively. At the instant the three particles A, B and C were located at (0,0) (3,4) , (4,3) (all in meter ) respectively in a co-ordinate system attached to the table.
(a) Find the velocity of A, B and C
(b) Find the angular velocity of the body.
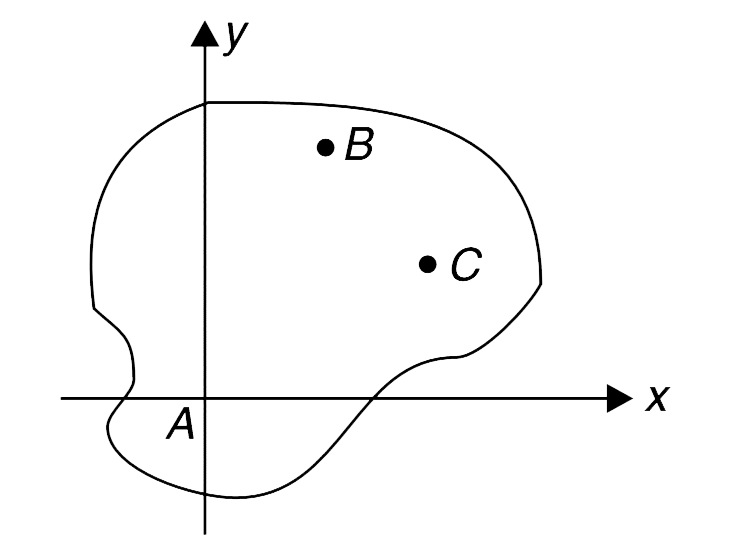 View Solution
View SolutionQuestion 57
There is a fixed half cylinder of radius R on a horizontal table. A uniform rod of length 2R leans against it as shown. At the instant shown, θ=30∘ and the right end of the rod is sliding with velocity v.
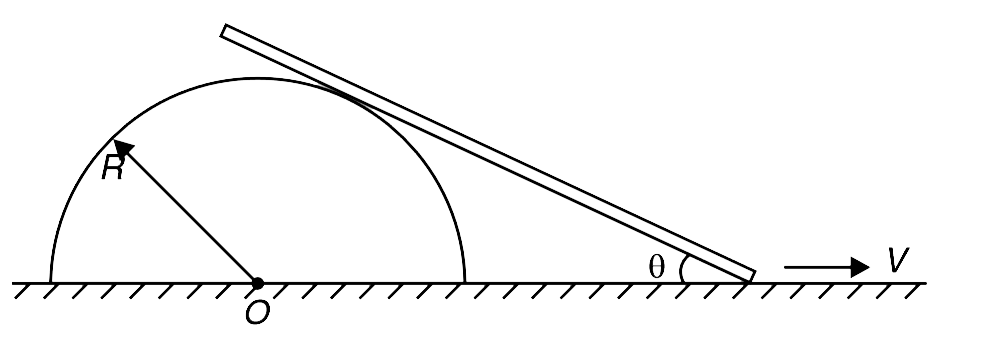
(a) Calculate the angular speed of the rod at this instant.
(b) Find the vertical component of the velocity of the centre of the rod at this instant.View SolutionQuestion 58
A disc of radius R is rolling without sliding on a horizontal surface at a constant speed of v

(a) What is speed of points A and B on the vertical diameter of the disc ? Given AB=R2
(b) After what time, for the first time, speed of point A becomes equal to present speed (i.e., the speed at the instant shown in the figure) of point B? View SolutionQuestion 59
A uniform disc of radius R=2√3m is moving on a horizontal surface without slipping. At some instant its angular velocity is ω=1 rad/s and angular acceleration is a α=√3rad/s2.

(a) Find acceleration of the top point A.
(b) Find acceleration of contact point B.
(c) Find co - oridnates (r,θ) for a point P which has zero accelerationView SolutionQuestion 61
AB is a non uniform plank of length L=4R with its centre of mass at C such that AC=R. It is placed on a step with its one end A supported by a cylinder of radius R as shown in figure. The centre of mass of the plank is just outside the edge of the step. The cylinder is slowly rolled on the lower step such that there is no slipping at any of its contacts. Calculate the distance through which the centre of the cylinder moves before the plank loses contact with the horizontal surface of the upper step.
 View Solution
View SolutionQuestion 63
A wall is inclined to a horizontal surface at an angle of 120∘ as shown. A rod AB of length L=0.75m is sliding with its two ends A and B on the horizontal surface and on the wall respectively. At the moment angle θ=20∘ (see figure), the velocity of end A is vA=1.5 m/s towards right. Calculate the angular speed of the rod at this instant. [Take cos40∘=0.766 ]
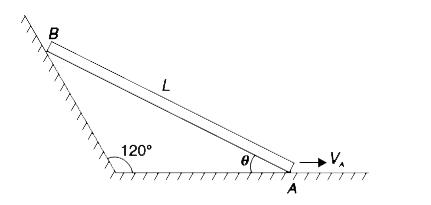 View Solution
View SolutionQuestion 64
In the figure the plank resting on two cylinders is horizontal. The plank is pulled to the right such that the centre of smaller cylinder moves with a constant velocity v. Friction is large enough to prevent slipping at all surfaces. Find-
(a) The velocity of the centre of larger cylinder.
(b) The ratio of accelerations of the points of contact of the two cylinders with the plank.
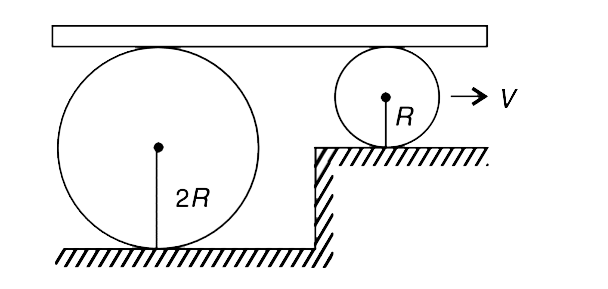 View Solution
View SolutionQuestion 66
A metallic plate has been fabricated by welding two semicircular discs - D1 and D2 of radii R and R2 respectively (fig. a). O and O' are the centre of curvature of the two discs and each disc has a mass 6m. The plate is in xy plane. Now the plate is folded along the y axis so as to bring the part OAB in yz plane. (fig. b). The plate is now set free to be able to rotate freely about the z – axis. A particle of mass m, moving with a velocity v in the xy plane along the line x=d hits the plate and sticks to it (d<R) . Just before collision speed of the particle was v.
(a)
(a) Find the moment of inertia of inertia of the plate about z axis.
(b) Find the angular speed of the plate after collision. View SolutionQuestion 67
There is a square plate of side length a. It is divided into nine identical squares each of side a3 and the central square is removed (see fig. (i)). Now each of the remaining eight squares of side length a3 are divided into nine identical squares and central square is removed from each of them (see fig. (ii)).
(a)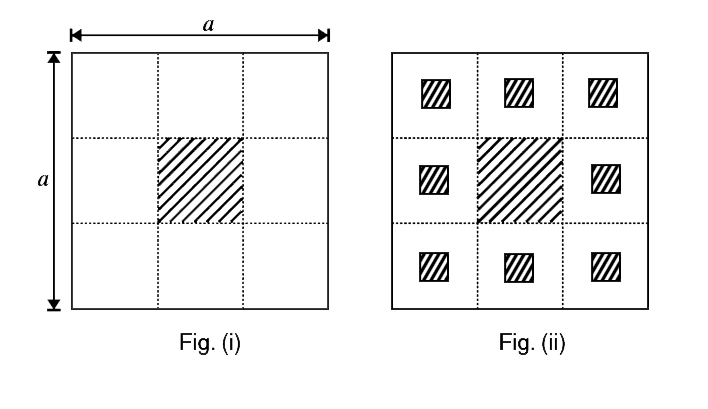
Mass of the plate with one big and eight small holes is M. Find its moment of inertia about an axis passing through its centre and perpendicular to its plane.View SolutionQuestion 68
ABC is an isosceles triangle right angled at A. Mass of the triangular plate is M and its equal sides are of length a. Find the moment of inertia of this plate about an axis through A perpendicular to the plane of the plate. Use the expression of moment of inertia for a square plate that you might have studied.
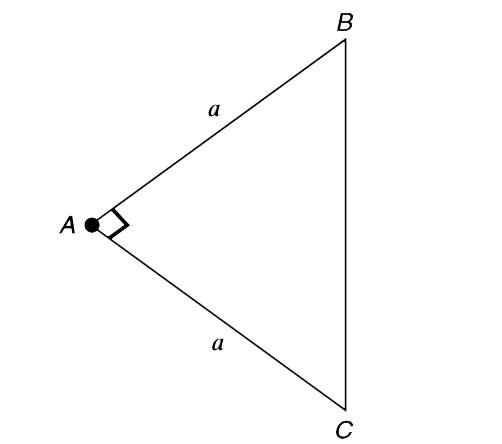 View Solution
View SolutionQuestion 70
A thin uniform spherical shell of radius R is bored such that the axis of the boring rod passes through the centre of the sphere. The boring rod is a cylinder of radius R2. Take the mass of the sphere before boring to be M.
(a) Find the mass of the leftover part
(b) Find the moment of inertia of the leftover part about the axis shown.
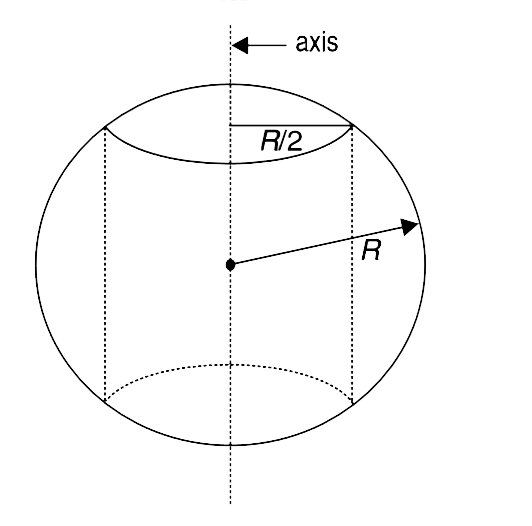 View Solution
View SolutionQuestion 72
In the arrangement shown in figure the cylinder of mass M is at rest on an incline. The string between the cylinder and the pulley (P) is horizontal. Find the minimum coefficient of friction between the incline and the cylinder which can keep the system in equilibrium. Also find the mass of the block. Assume no friction between the pulley (P) and the string.
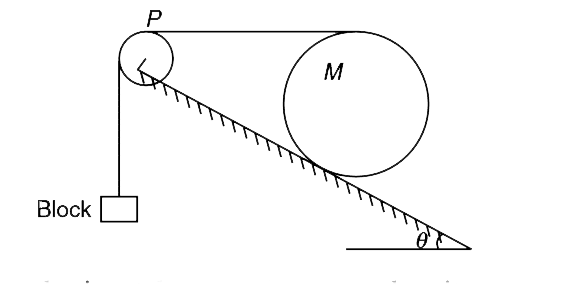 View Solution
View SolutionQuestion 73
A horizontal stick of mass m has its right end attached to a pivot on a wall, while its left end rests on the top of a cylinder of mass m which in turn rests on an incline plane inclined at an angle θ. The stick remains horizontal. The coefficient of friction between the cylinder and both the plane and the stick is μ. Find the minimum value of μ as function of θ for which the system stays in equilibrium.
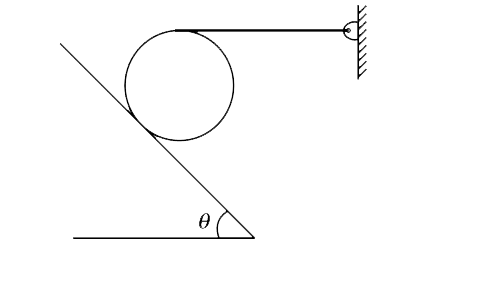 View Solution
View SolutionQuestion 74
Consider the object shown in the figure. It consist of a solid hemisphere of mass M and radius R. There is a solid rod welded at its centre. The object is placed on a flat surface so that the rod is vertical. Mass of the rod per unit length is M2R. What is the maximum length of the rod that can be welded so that the object can perform oscillations about the position shown in diagram?
Note : Centre of mass of a solid hemisphere is at a distance of 3R8 from its base.
 View Solution
View SolutionQuestion 76
The ladder shown in the figure is light and stands on a frictionless horizontal surface. Arms AB and BC are of equal length and M and N are their mid points. Length of MN is half that of AB. A man of mass M is standing at the midpoint of BM. Find the tension in the mass less rod MN. Consider the man to be a point object.
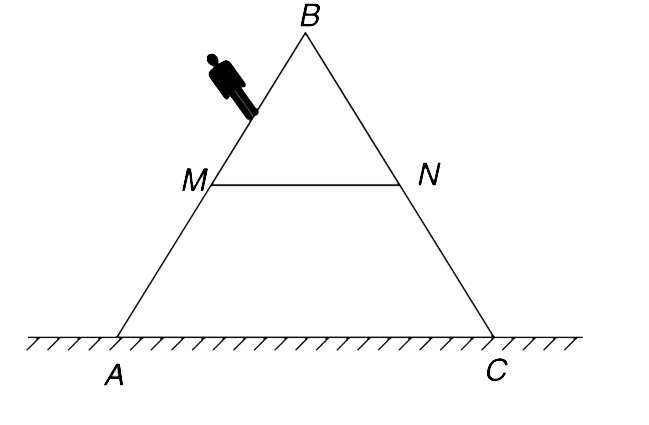 View Solution
View SolutionQuestion 77
A uniform metal sheet of mass M has been folded to give it L shape and it is placed on a rough floor as shown in figure. Wind is blowing horizontally and hits the vertical face of the sheet as shown. The speed of air varies linearly from zero at floor level to v0 at height L from the floor. Density of air is ρ. Find maximum value of v0 for which the sheet will not topple. Assume that air particles striking the sheet come to rest after collision, and that the friction is large enough to prevent the sheet from sliding
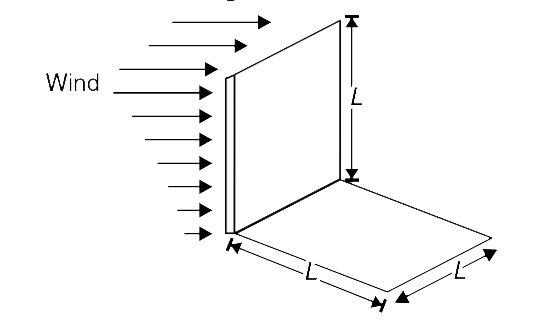 View Solution
View SolutionQuestion 79
A spool is kept in equilibrium on an incline plane as shown in figure. The inner and outer radii of the spool are in ratio rR=12. The force applied on the thread (wrapped on part of radius r) is horizontal. Find the angle that the force applied by the incline on the spool makes with the vertical.
[Take tan−1(√35)≅19∘ ]
 View Solution
View SolutionQuestion 81
A L shaped, uniform rod has its two arms of length l and 2l. It is placed on a horizontal table and a string is tied at the bend. The string is pulled horizontally so that the rod slides with constant speed. Find the angle θ that the longer side makes with the string. Assume that the rod exerts uniform pressure at all points on the table.
 View Solution
View SolutionQuestion 82
A uniform meter stick AB of mass M is lying in state of rest on a rough horizontal plane. A small block of mass m is placed on it at its centre C. A variable force F is applied at the end B of the stick so as to rotate the stick slowly about A in vertical plane. The force F always remains perpendicular to the length of the stick. The stick is raised to θ=60∘ and it was observed that neither the end A slipped on the ground nor the block of mass m slipped on the stick.

(a) F1 is force applied by the stick on the block. Plot the variation of F1 with θ(0≤θ≤60∘).
(b) What must be the minimum coefficient of friction between the block and the stick.
(c) f is the friction force acting at end A of the stick. Plot variation of fvsθ(0∘≤θ≤60∘).View SolutionQuestion 83
A ladder of mass M and length L stays at rest against a smooth wall. The coefficient of friction between the ground and the ladder is μ
(a) Let Fwall, W and Fg be the force applied by wall, weight of the ladder and force applied by ground on the ladder. Argue to show that the line of action of these three forces must intersect.
(b) Using the result obtained in (a) show that line of action of Fg makes an angle tan−1(2tanθ) with the horizontal ground where θ is the angle made by the ladder with the ground.
(c) Find the smallest angle that the ladder can make with the ground and not slip.
(d) You climb up the ladder, your presence makes the ladder more likely to slip. Where are you at A or B? C is the centre of mass of the ladder.
 View Solution
View SolutionQuestion 84
A uniform rod AB has mass M and length L. It is in equilibrium supported in vertical plane by three identical springs as shown in figure. The springs are connected at A, C and D such that AC=CD=L3. Assume that the springs are very stiff and the angle a made by the rod with the horizontal in equilibrium position is very small. (All springs are nearly vertical). Calculate the tension in the three springs.
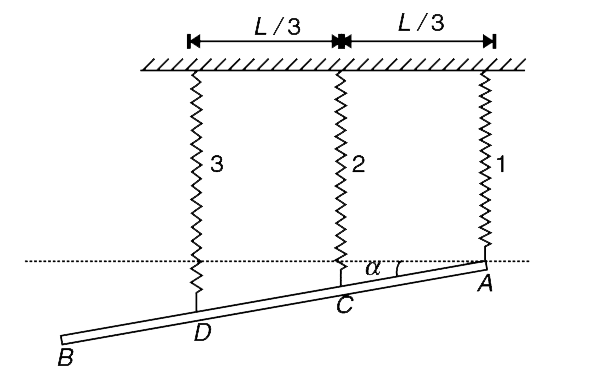 View Solution
View SolutionQuestion 85
A uniform rod of length b can be balanced as shown in figure. The lower end of the rod is resting against a vertical wall. The coefficient of friction between the rod and the wall and that between the rod and the support at A is μ. Distance of support from the wall is a.
(a) Find the ratio ab if the maximum value of θ is θ1.
(b) Find the ratio ab if the minimum value of θ is θ2.
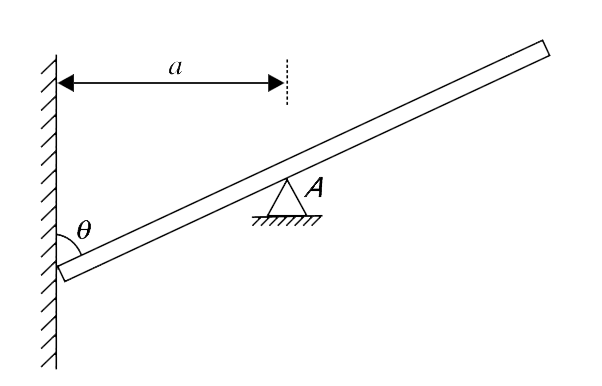 View Solution
View SolutionQuestion 86
A uniform rectangular block is moving to the right on a rough horizontal floor (the block is retarding due to friction). The length of the block is L and its height is h. A small particle (A) of mass equal to that of the block is stuck at the upper left edge. Coefficient of friction between the block and the floor is μ=23. Find the value of h (in terms of L) if the normal reaction of the floor on the block effectively passes through the geometrical centre (C) of the block.
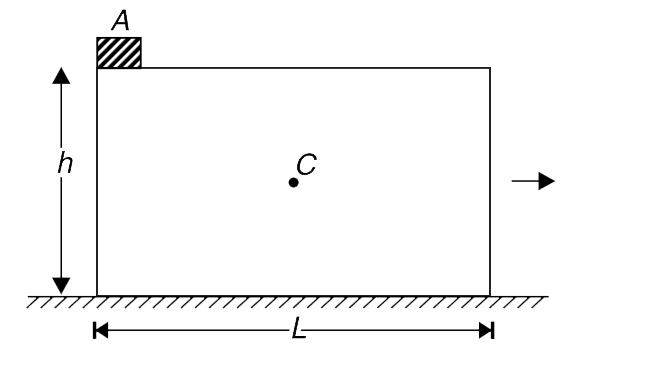 View Solution
View SolutionQuestion 87
A uniform cubical block of mass M and side length L is lying on the edge of a rough table with 14th of its edge overhanging. When a small block of mass m is placed on its top surface at the right edge (see fig.), the cube is on verge of toppling. The block of mass m is given a sharp horizontal impulse so that it acquires a velocity towards B. The small block moves on the top surface and falls on the other side. What is maximum coefficient of friction between the small block and the cube so that the cube does not rotate as the block moves over it. Assume that the friction between the cube and the table is large enough to prevent sliding of the cube on the table.
 View Solution
View SolutionQuestion 88
A uniform rod of mass M and length L is hinged at its end to a wall so that it can rotate freely in a horizontal plane. When the rod is perpendicular to the wall a constant force F starts acting at the centre of the rod in a horizontal direction perpendicular to the rod. The force remains parallel to its original direction and acts at the centre of the rod as the rod rotates. (Neglect gravity).
(a) With what angular speed will the rod hit the wall ?
(b) At what angle θ (see figure) the hinge force will make a 45∘ angle with the rod ?
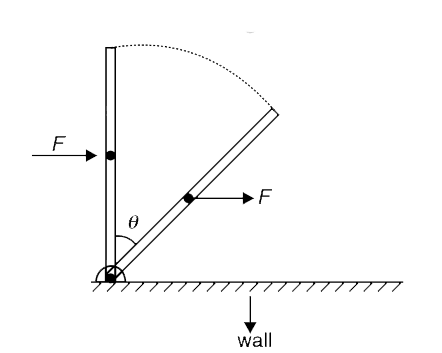 View Solution
View SolutionQuestion 89
A rod of mass M=5kg and length L=1.5m is held vertical on a table as shown. A gentle push is given to it and it starts falling. Friction is large enough to prevent end A from slipping on the table.
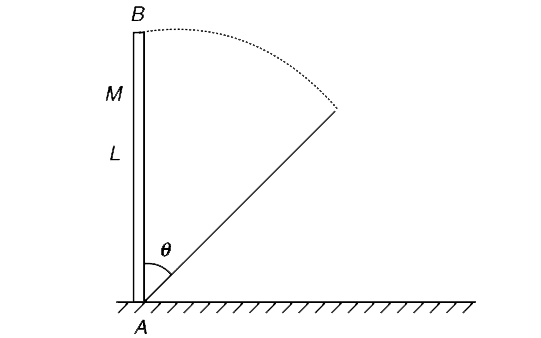
(a) Find the sum of linear momentum of all the particles of the rod when it rotates through an angle θ=37∘
(b) Find the friction force and normal reaction force by the table on the rod, when θ=37∘
(c) Find value of angle q when the friction force becomes zero.
[tan37∘=34 and g=10m/s] View SolutionQuestion 90
(a) In the system shown in figure 1, the uniform rod of length L and mass m is free to rotate in vertical plane about point O. The string an pulley are mass less. The block has mass equal to that of the rod. Find the acceleration of the block immediately after the system is released with rod in horizontal position.
(b) System shown in figure 2 is similar to that in figure 1 apart from the fact that rod is mass less and a block of mass m is attached to the centre of the rod with the help of a thread. Find the acceleration of both the blocks immediately after the system is released with rod in horizontal position.
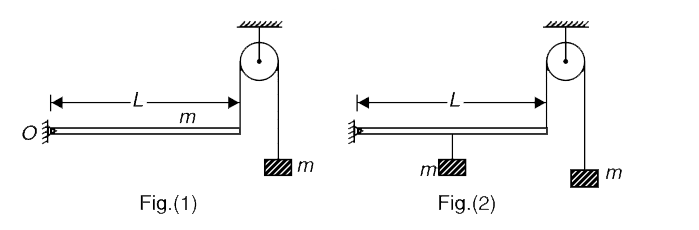 View Solution
View SolutionQuestion 91
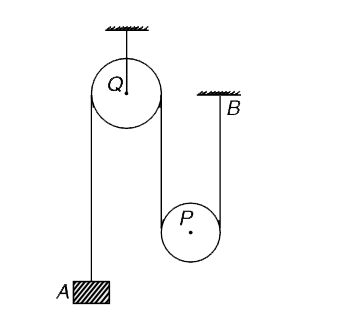
A light thread is wrapped tightly a few turns around a disc P of mass M. One end of the thread is fixed to the ceiling at B. The other end of the thread is passed over a mass less pulley (Q) and carries a block of mass M. All segment of the thread (apart from that on the pulley and disc) are vertical when the system is released. Find the acceleration of block A. On which object – the block A or the ceiling at B – does the thread exert more force ?View SolutionQuestion 92
An equilateral triangle is made from three mass less rods, each of length l. Two point masses m are attached to two vertices. The third vertex is hinged and triangle can swing freely in a vertical plane as shown. It is released the position shown with one of the rods vertical. Immediately after the system is released, find –
(a) tensions in all three rods (specify tension or compression),
(b) accelerations of the two masses
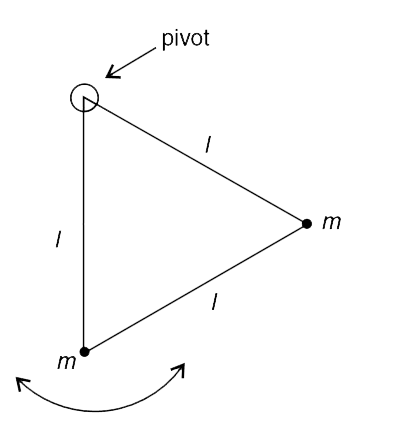 View Solution
View SolutionQuestion 94
A disc is free to rotate about an axis passing through its centre and perpendicular to its plane. The moment of inertia of the disc about its rotation axis is I. A light ribbon is tightly wrapped over it in multiple layers. The end of the ribbon is pulled out at a constant speed of u. Let the radius of the ribboned disc be R at any time and thickness of the ribbon be d(<<R). Find the force (F) required to pull the ribbon as a function of radius R.
 View Solution
View SolutionQuestion 95
A uniform rod of mass M and length L is hinged at its lower end on a table. The rod can rotate freely in vertical plane and there is no friction at the hinge. A ball of mass M and radius R=L3 is placed in contact with the vertical rod and a horizontal force F is applied at the upper end of the rod.
(a) Find the acceleration of the ball immediately after the force starts acting.
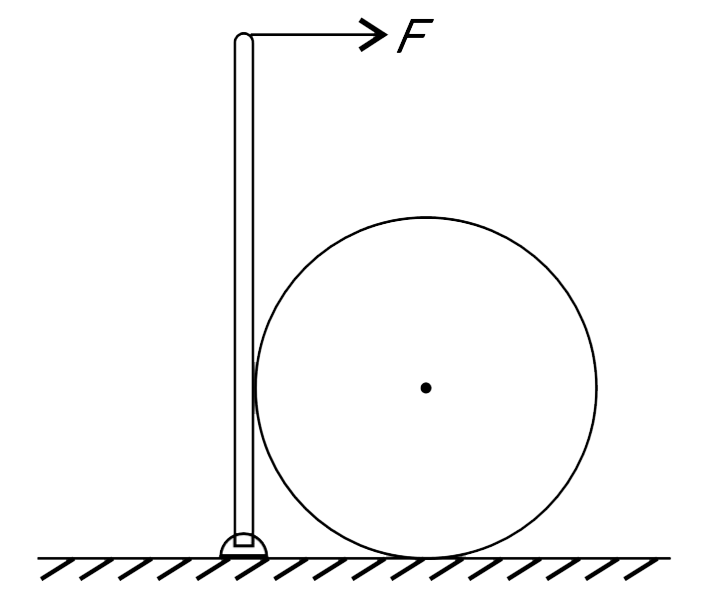
(b) Find the horizontal component of hinge force acting on the rod immediately after force F starts acting. View SolutionQuestion 96

A ring of mass M and radius R is held at rest on a rough horizontal surface. A rod of mass M and length L=2√3R is pivoted at its end A on the horizontal surface and is supported by the ring. There is no friction between the ring and the rod. The ring is released from this position. Find the acceleration of the ring immediately after the release if θ=60∘. Assume that friction between the ring on the horizontal surface is large enough to prevent slipping of the ring. View SolutionQuestion 98
A uniform solid hemisphere A of mass M radius R is joined with a thin uniform hemispherical shell B of mass M and radius R (see fig.). The sphere thus formed is placed inside a fixed box as shown. The floor , as well as walls of the box are smooth. On slight disturbance, the sphere begins to rotate. Find its maximum angular speed (ω) and maximum angular acceleration (α0) during the subsequent motion. Do the walls of the box apply any force on the sphere while it rotates ?
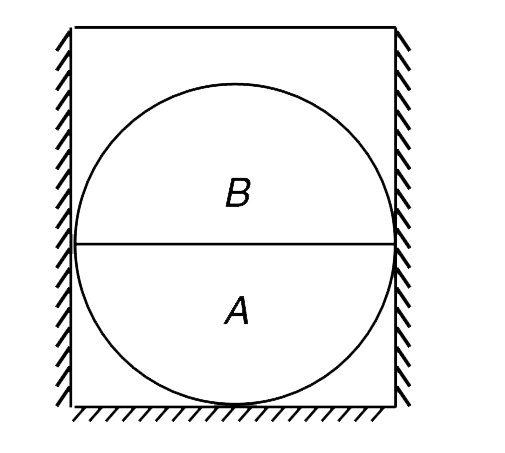 View Solution
View SolutionQuestion 99

In the arrangement shown, the double pulley has a mass M and the two mass less threads have been tightly wound on the inner (radius =r) and outer circumference (radius R=2r). The block shown has a mass 4 M. The moment of inertia of the double pulley system about a horizontal axis passing through its centre and perpendicular to the plane of the figure is I=Mr22.
(a) Find the acceleration of the center of the pulley after the system is released.
(b) Two seconds after the start of the motion the string holding the block breaks. How long after this the pulley will stop ascending? View SolutionQuestion 100
A thread is tightly wrapped on two pulleys as shown in figure. Both the pulleys are uniform disc with upper one having mass M and radius R being free to rotate about its central horizontal axis. The lower pulley has mass m and radius r and it is released from rest. It spins and falls down. At the instant of release a small mark (A) was at the top point of the lower pulley.
(a) After what minimum time (t0) the mark will again be at the top of the lower pulley?
(b) Find acceleration of the mark at time t0.
(c) Is there any difference in magnitude of acceleration of the mark and that of a point located on the circumference at diametrically opposite end of the pulley.
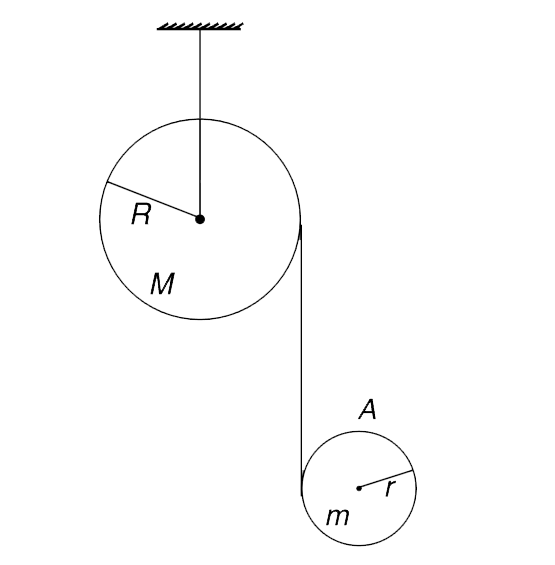 View Solution
View SolutionQuestion 101
A point mass m=1kg is attached to a point P on the circumference of a uniform ring of mass M=3kg and radius R=2.0m. The ring is placed on a horizontal surface and is released from rest with line OP in horizontal position (O is centre of the ring). Friction is large enough to prevent sliding. Calculate the following quantities immediately after the ring is released-
(a) angular acceleration (α) of the ring,
(b) normal reaction of the horizontal surface on the ring and
(c) the friction force applied by the surface on the ring.
[Take g=10m/s2 ]
 View Solution
View SolutionQuestion 102
A light thread has been tightly wrapped around a disc of mass M and radius R. The disc has been placed on a smooth table, lying flat as shown.
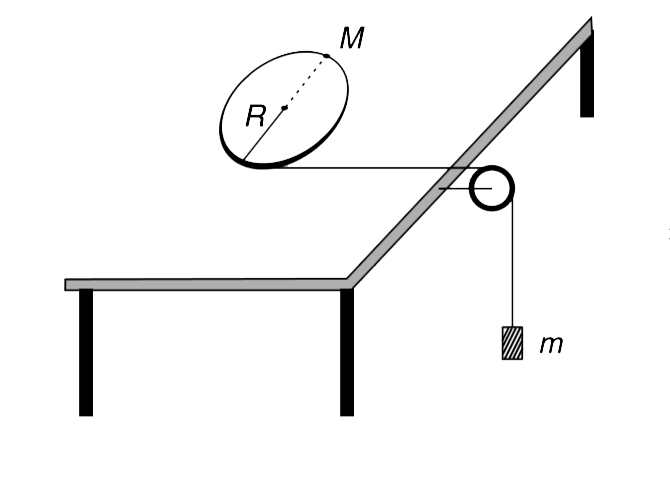
The other end of the string has been attached to a mass m as shown. The system is released from rest. If m=M, which point of the disc will have zero acceleration, immediately after the system is released? View SolutionQuestion 103
A spool has the shape shown in figure. Radii of inner and outer cylinders are R and 2 R respectively. Mass of the spool is 3m and its moment of inertia about the shown axis is 2mR2. Light threads are tightly wrapped on both the cylindrical parts. The spool is placed on a rough surface with two masses m1=m and m2=2m connected to the strings as shown. The string segment between spool and the pulleys P1 and P2 are horizontal. The centre of mass of the spool is at its geometrical centre. System is released from rest.
(a) What is minimum value of coefficient of friction between the spool and the table so that it does not slip?
(b) Find the speed of m1 when the spool completes one rotation about its centre.
 View Solution
View SolutionQuestion 104
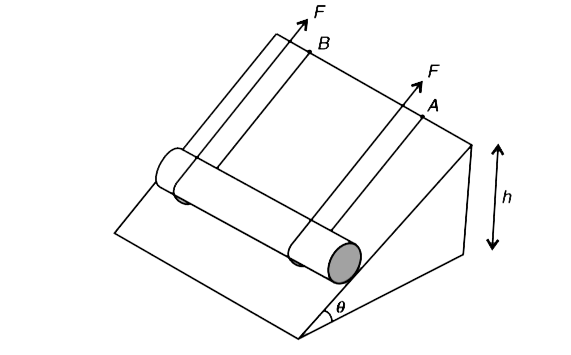
A heavy uniform log of mass M is pulled up an incline surface with the help of two parallel ropes as shown in figure. The ropes are secured at point A and B. The height of the incline is h and its inclination is θ.
(a) Find the minimum force F0 needed to roll the log up the incline.
(b) Find the work done by the force in moving the log from the bottom to the top of the incline if the applied force is F=2F0 View SolutionQuestion 105
In the figure shown, the light thread is tightly wrapped on the cylinder and masses of plank and cylinder are same each equal to m. An external agent begins to pull the plank to the right with a constant force F. The friction between the plank and the cylinder is large enough to prevent slipping. Assume that the length of the plank is quite large and the cylinder does not fall off it for the time duration concerned.
(a) Find the acceleration of the cylinder. (Hint : don’t write any equations)
(b) Find the kinetic energy of the system after time t.
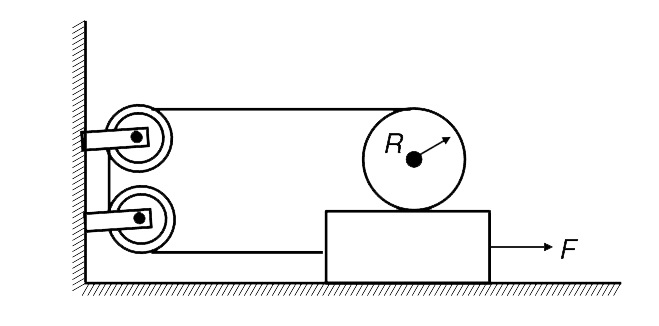 View Solution
View SolutionQuestion 106
A disc of radius r=0.1m is rolled from a point A on a track as shown in the figure. The part AB of the track is a semi-circle of radius R in a vertical plane. The disc rolls without sliding and leaves contact with the track at its highest point B. Flying through the air it strikes the ground at point C. The velocity of the center of mass of the disc makes an angle of 30∘ below the horizontal at the time of striking the ground. At the same instant, velocity of the topmost point P of the disc is found to be 6m/s (Take g=10m/s2 ).

(a) Find the value of R.
(b) Find the velocity of the center of mass of the disc when it strikes the ground.
(c) Find distance AC.View SolutionQuestion 107
A trough has two identical inclined segments and a horizontal segment. A ball is released on the top of one inclined part and it oscillates inside the trough. Friction is large enough to prevent slipping of the ball. Time period of oscillation is T. Now the liner dimension of each part of the trough is enlarged four times. Find the new time period of oscillation of the ball.
 View Solution
View SolutionQuestion 108
A uniform cylinder is lying on a rough sheet of paper as shown in fig. The strip is pulled horizontally to the right with a constant acceleration of a0=6m/s2. Initially the cylinder is located at a distance of L=10m from the left end of the strip. Find the velocity of the centre of the cylinder at the instant it moves off the edge of the strip. Assume that the cylinder does not slip.
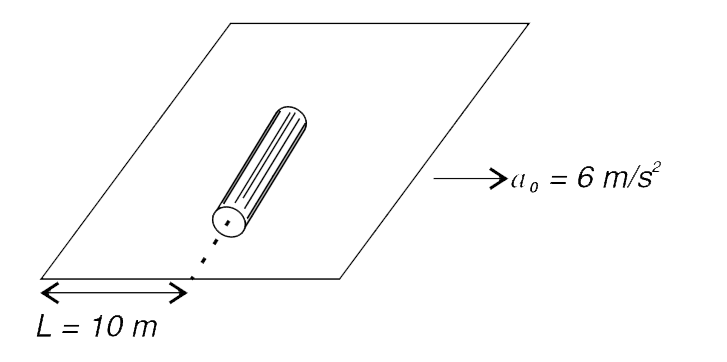 View Solution
View SolutionQuestion 109
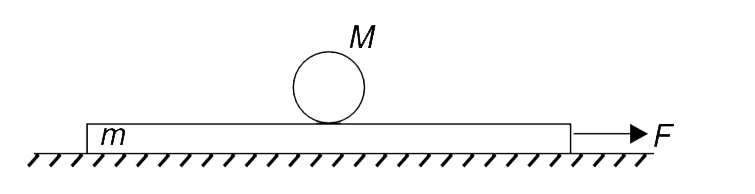
A hollow pipe of mass M=6kg rests on a plate of mass m=1.5kg . The thickness of the pipe is negligible. The coefficient of friction at all contacts is μ=0.2. The system is initially at rest. A horizontal force F of magnitude 25N is applied on the plate as shown in figure. Will the cylinder slide on the plate? Find the acceleration of the centre of the cylinder. View SolutionQuestion 110
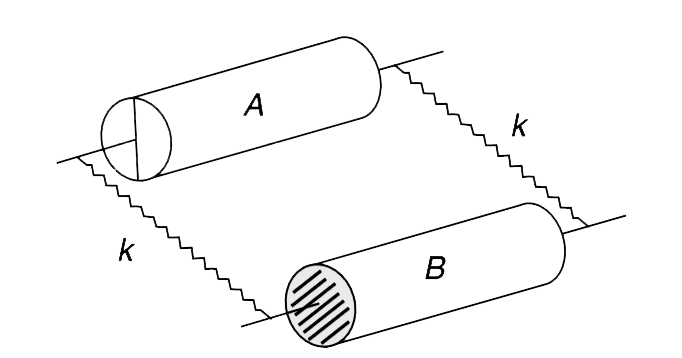
A hollow cylindrical pipe A has mass M and radius R. With the help of two identical springs (each of force constant k) it is connected to solid cylinder B having mass M and radius R. The springs are connected symmetrically to the axle of the cylinders. Moment of inertia of the two Bodies A and B about their axles are IA=MR2 and IB=12MR2 respectively. Cylinders are pulled apart so as to stretch the springs by x0 and released. During subsequent motion the cylinders do not slip.
(a) Find acceleration of the centre of mass of the system immediately after it is released.
(b) Find the distance travelled by cylinder A by the time it comes to rest for the first time after being released.View SolutionQuestion 111
Two identical uniform thin rods have been connected at right angles to form a ‘T’ shape. One end of a rod is connected to the centre of the other rod. Length of each rod is L. The upside down ‘T’ can swing like a pendulum about a horizontal axis passing through the top end (see fig.). Axis is perpendicular to plane of the fig. The speed of the meeting point of the two rods is u=2√gL when it is at its lowest position. Calculate the angular acceleration of the ‘T’ shaped object when it is at extreme position of its oscillation.
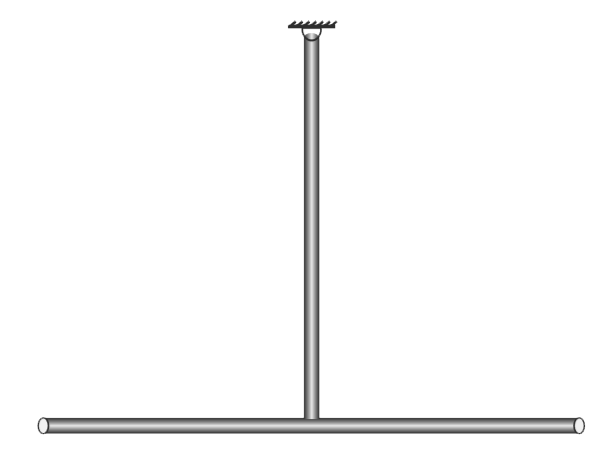 View Solution
View SolutionQuestion 112
A uniform rod of mass M and length L is hinged at its lower end so as to rotate freely in the vertical plane of the fig. There is a small tight fitting the hinged end. A small mass less pin welded to the rod supports the bead. The system is released from the vertical position shown. It was observed that the bead just begins to slide on the rod when the rod becomes horizontal.
(a) Find the normal contact force between the rod and the bead when the rod gets horizontal. What is the direction of this force?
(b) Find the coefficient of friction between the bead and rod.
 View Solution
View SolutionQuestion 113
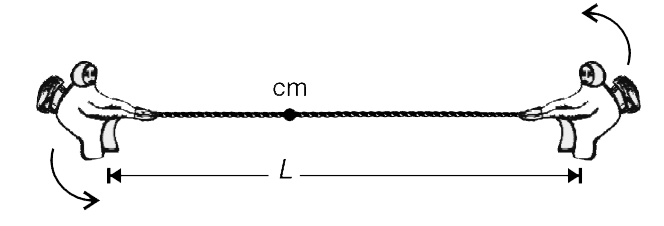
Two astronauts having mass of 75kg and 50kg are connected by a rope of length L=10m and negligible mass. They are in space, orbiting their centre of mass at an angular speed of ω0=5rad/s. The centre of mass itself is moving uniformly in space at a velocity of 10m/s. By pulling on the rope, the astronauts shorten the distance between them to L2=5m . How much work is done by the astronauts in shortening the distance between them ? Assuming that the astronauts are athletic and each of them can generate a power of 500 watt, is it possible for the two astronauts to reduce the distance between them to 5m, within a minute? View SolutionQuestion 114
In the figure shown a plank of mass m is lying at rest on a smooth horizontal surface. A cylinder of same mass m and radius r is rotated to an angular speed w0 and then gently placed on the plank. It is found that by the time the slipping between the plank and the cylinder cease, 50% of total kinetic energy of the cylinder and plank system is lost. Assume that plank is long enough and um is the coefficient of friction between the cylinder and the plank.
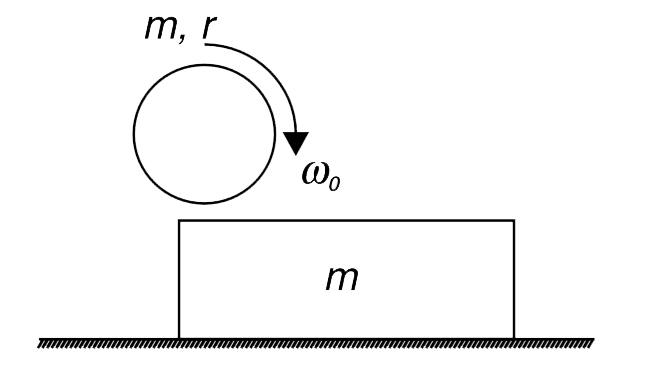
(a) Find the final velocity of the plank.
(b) Calculate the magnitude of the change in angular momentum of the cylinder about its centre of mass.
(c) Distance moved by the plank by the time slipping ceases between cylinder and plank. View SolutionQuestion 115
A horizontal turn table of mass 90kg is free to rotate about a vertical axis passing through its centre. Two men –1 and 2 of mass 50kg and 60kg respectively are standing at diametrically opposite point on the table. The two men start moving towards each other with same speed (relative to the table) along the circumference. Find the angle rotated by table by the time the two men meet. Treat the men as point masses.
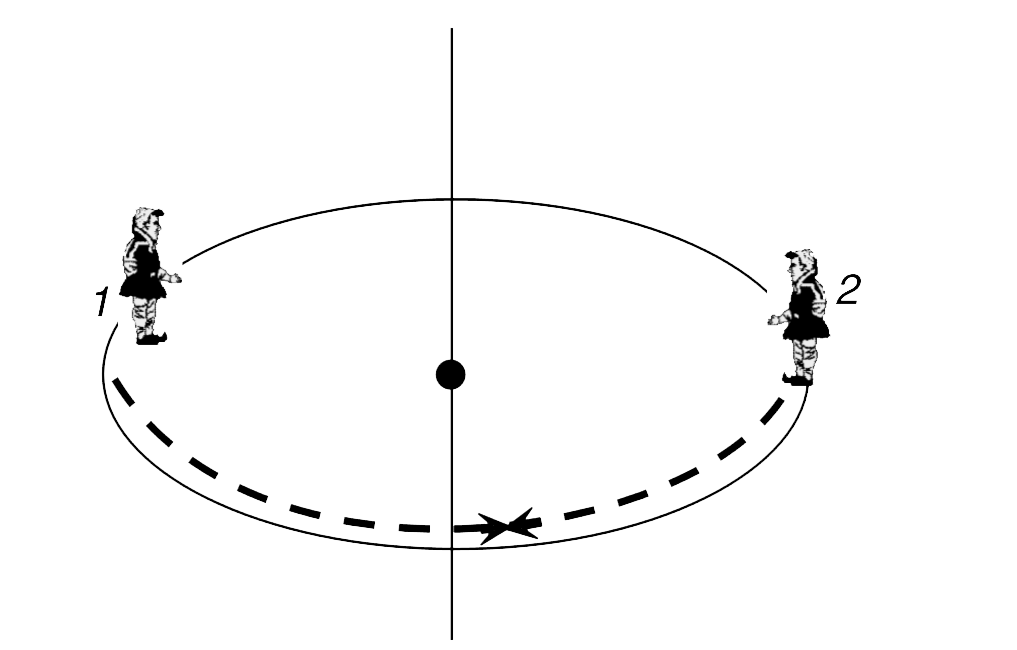 View Solution
View SolutionQuestion 116
A L shaped uniform rod has both its sides of length l. Mass of each side is m. The rod is placed on a smooth horizontal surface with its side AB horizontal and side BC vertical. It tumbles down from this unstable position and falls on the surface. Find the speed with which end C of the rod hits the surface.
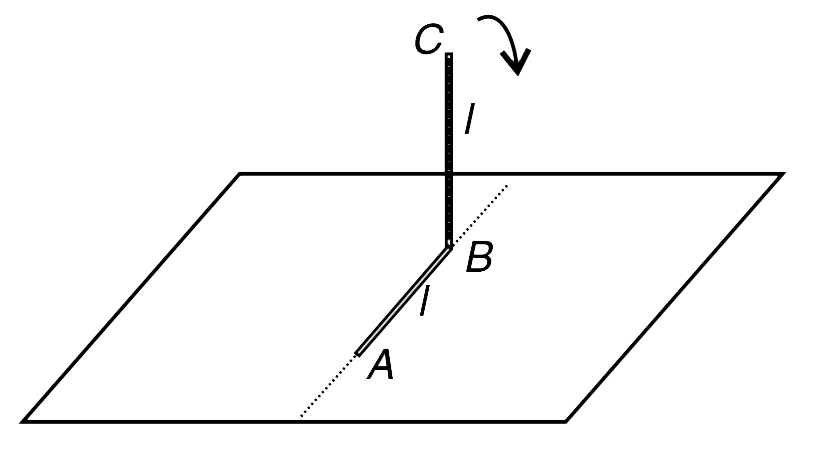 View Solution
View SolutionQuestion 117
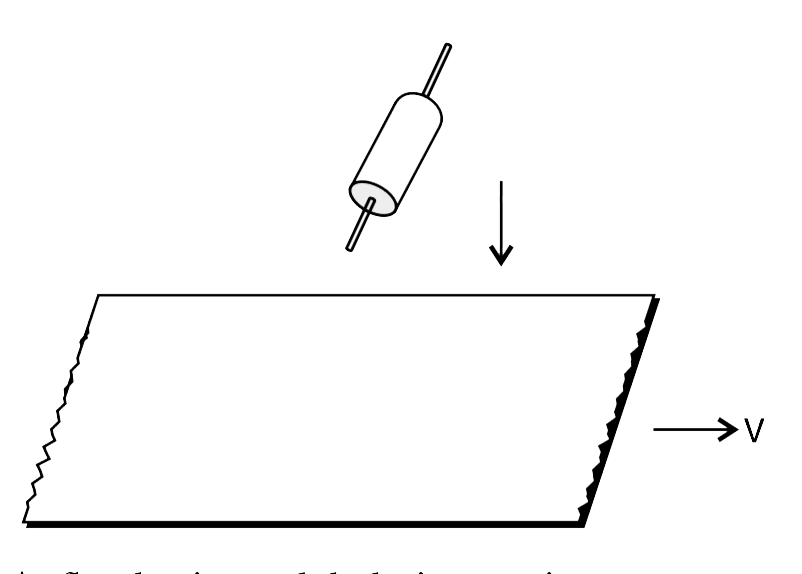
A flat horizontal belt is running at a constant speed V. There is a uniform solid cylinder of mass M which can rotate freely about an axle passing through its centre and parallel to its length. Holding the axle parallel to the width of the belt, the cylinder is lowered on to the belt. The cylinder begins to rotate about its axle and eventually stops slipping. The cylinder is, however, not allowed to move forward by keeping its axle fixed. Assume that the moment of inertia of the cylinder about its axle is 12MR2 where M is its mass and R its radius and also assume that the belt continues to move at constant speed. No vertical force is applied on the axle of the cylinder while holding it.
(a) Calculate the extra power that the motor driving the belt has to spend while the cylinder gains rotational speed. Assume coefficient of friction =μ.
(b) Prove that 50% of the extra work done by the motor after the cylinder is placed over it, is dissipated as heat due to friction between the belt and the cylinderView SolutionQuestion 118
A uniform disc of mass M and radius R is rotating freely about its central vertical axis with angular speed w0. Another disc of mass m and radius r is free to rotate about a horizontal rod AB. Length of the rod AB isL(<R) and its end A is rigidly attached to the vertical axis of the first disc. The disc of mass m, initially at rest, is placed gently on the disc of mass M as shown in figure. Find the time after which the slipping between the two discs will cease. Assume that normal reaction between the two discs is equal to mg. Coefficient of friction between the two discs is μ.
 View Solution
View SolutionQuestion 119
P is a fixed smooth cylinder of radius R and Q is a disc of mass M and radius R. A light thread is tightly wound on Q and its end is connected to a rope ABC. The rope has a mass m and length πR2 and is initially placed on the cylinder with its end A at the top. The system is released from rest. The rope slides down the cylinder as the disc rolls without slipping. The initial separation between the disc and the cylinder was L=πR2 (see fig). Find the speed with which the disc will hit the cylinder. Assume that the rope either remains on the cylinder or remains vertical, it does not fly off the cylinder.
 View Solution
View SolutionQuestion 120
A uniform cube of mass M and side length a is placed at rest at the edge of a table. With half of the cube overhanging from the table, the cube begins to roll off the edge. There is sufficient friction at the edge so that the cube does not slip at the edge of the table. Find -
(a) the angle θ0 through which the cube rotates before it leaves contact with the table.
(b) the speed of the centre of the cube at the instant it breaks off the table.
(c) the rotational kinetic energy of the cube at the instant its face AB becomes horizontal.
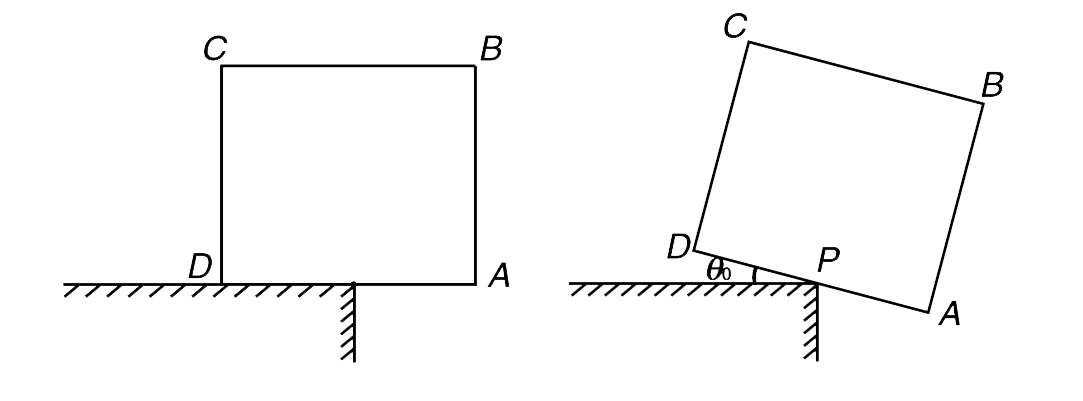 View Solution
View SolutionQuestion 121
A uniform frictionless ring of mass M and radius R, stands vertically on the ground. A wall touches the ring on the left and another wall of height R touches the ring on right (see figure).There is a small bead of mass m positioned at the top of the ring. The bead is given a gentle push and it being to slide down the ring as shown. All surfaces are frictionless.
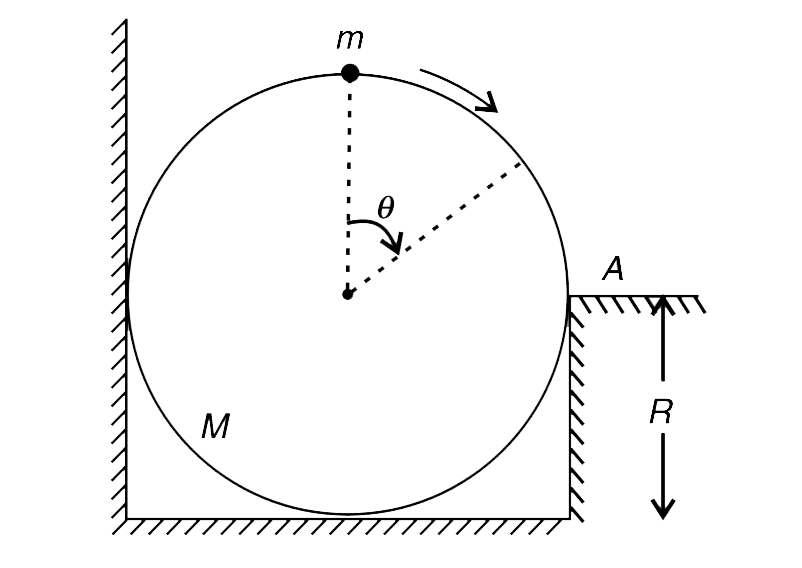
(a) As the bead slides, up to what value of angle θ the force applied by the ground on the ring is larger than Mg?
(b) Write the torque of force applied by the bead on the ring about point A as function of θ.
(c) What is the maximum possible value of torque calculated in (b)? Using this result tell what is the largest value of mM for which the ring never rises off the ground ? View SolutionQuestion 122
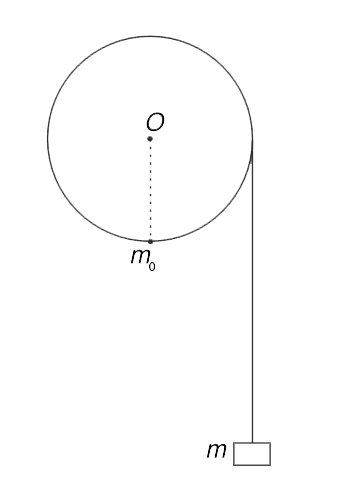
A uniform disc shaped pulley is free to rotate about a horizontal axis passing through the centre of the pulley. A light thread is tightly wrapped over it and supports a mass m at one of its end. A small particle of mass m0=2m is stuck at the lowest point of the disc and the system is released from rest. Will the particle of mass m0 climb to the top of the pulley? View SolutionQuestion 123

AOB is a frictionless parabolic track in vertical plane. The equation of parabolic track can be expressed as y=32Hx2 for co-ordinate system shown in the figure. The end B of the track lies at y=H2. When a uniform small ring is released on the track at A it was found to attain a maximum height of h1, above the ground after leaving the track at B. There is another track DEF which is in form of an arc of a circle of radius H subtending an angle an angle of 150∘ at the centre. The radius of the track at D is horizontal. The same ring is released on this track at point D and it rolls without sliding. The ring leaves the track at F and attains a maximum height of h2 above the ground. Find the ratio h1h2.View SolutionQuestion 124
A uniform sphere of radius R has a spherical cavity of radius R2 (see figure). Mass of the sphere with cavity is M. The sphere is rolling without sliding on a rough horizontal floor [the line joining the centre of sphere to the centre of the cavity remains in vertical plane]. When the centre of the cavity is at lowest position, the centre of the sphere has horizontal velocity V. Find:
(a) The kinetic energy of the sphere at this moment.
(b) The velocity of the centre of mass at this moment.
(c) The maximum permissible value of V ( in the position shown ) which allows the sphere to roll without bouncing
 View Solution
View SolutionQuestion 125
A uniform ball of mass M and radius R can rotate freely about any axis through its centre. Its angular velocity vector is directed along positive x axis. A bullet is fired along negative Z direction and it pierces through the ball along a line that is at a perpendicular distancer(≤R) from the centre of the ball. The bullet passes quickly and its net effect is that it applies an impulse on the ball. Mass of the bullet is m and its velocity charges from u tov(≤u) as it passes through the ball. As a result the ball stops rotating about X axis and begins to rotate about y axis. The angular speed of the ball before and after the hit is ω. Find r.
 View Solution
View SolutionQuestion 126
A uniform square plate ABCD has mass M side length a. It is sliding on a horizontal smooth surface with a velocity of→v=v0(4ˆi+2ˆj). There is no rotation. Vertex A of the plate is suddenly fixed by a nail. Calculate the velocity of centre of the plate immediately after this
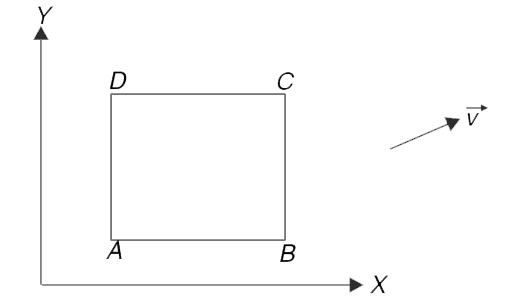 View Solution
View SolutionQuestion 127
Two discs A and B are moving with their flat circular surface on a smooth horizontal surface. Mass, radius and velocity of the two discs are −mA=2M,mB=M,rA=R,=2R,vA=v, and vB=2v. The velocities of the two discs are oppositely directed so that they just cannot avoid collision and stick to each other (see figure)
(a) Find the angular speed of the composite system after collision
(b) Find loss in kinetic energy due to collision
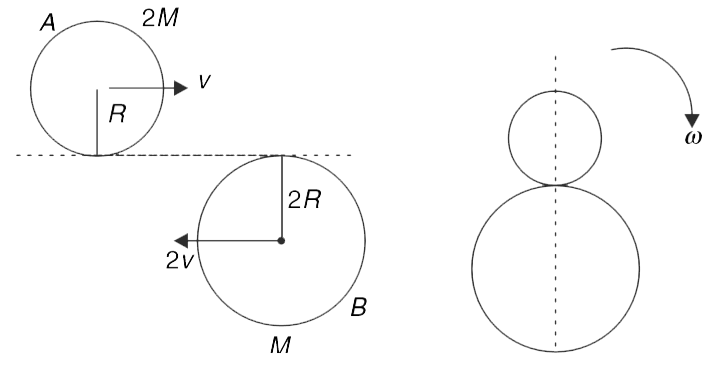 View Solution
View SolutionQuestion 128
A uniform rod of mass M and length 2L lies on a smooth horizontal table. There is a smooth peg O fixed on the table. One end of the rod is kept touching the peg as shown in the figure. An impulse J is imparted to the rod at its other end. The impulse is horizontal and perpendicular to the length of the rod. Find the magnitude of impulse experienced by the peg.
 View Solution
View SolutionQuestion 129
A uniform rod of mass M and length l is hinged at point O and is free to rotate on a horizontal smooth surface. Point O is at a distance of l4 from one end of the rod. A sharp impulse P0=2√130kgm/s is applied along the surface at one end of the rod as shown in figure [tanθ=97]
(a) Find the angular speed of the rod immediately after the hit
(b) Find the impulse on the rod due to the hinge.
 View Solution
View SolutionQuestion 130
Four thin rods of length L = 1.0 m each are joined to form a square ABCD. The opposite vertices of the square are joined by mass less rods AC and BD. This square frame is mounted on a horizontal axis through its centre so that the frame can rotate freely in the vertical plane. Masses of rods AB and BC are m=2kg each and the rod AD and DC have mass M=4kg each. A monkey of mass m0=12kg is at rest on the horizontal rod AD and keeps the system in equilibrium. The monkey takes a sudden jump and rises to a height H from its initial position. Calculate minimum value of H so that the square frame is able to complete a rotation about its central axis. Assume no further contact between monkey and the frame.
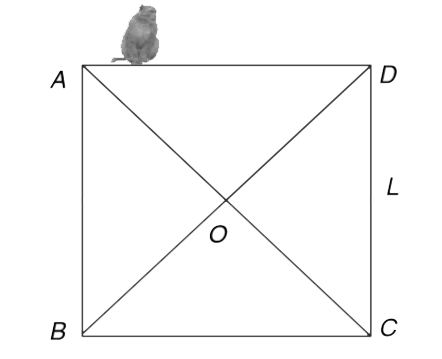 View Solution
View SolutionQuestion 131
A frustum has been mounted with its axis vertical. It has a height h and radii of its upper and lower cross sections are R and r respectively. A particle is projected with horizontal velocity v0 along its upper brim. The particle spirals down the inner surface and leaves the lower face at point B. The inner wall of the frustum is smooth.
(a) Find the vertical component of velocity of the particle as it leaves the frustum at B.
(b) Find minimum value of h for which the particle will never come out of the frustum.
Take r=R2 for solving this part of the problem.
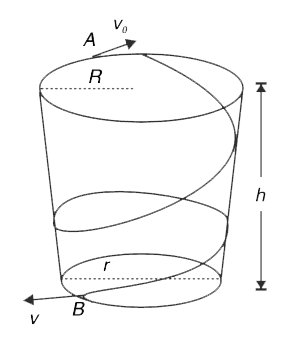 View Solution
View SolutionQuestion 132
A uniform thin stick of mass M=24kg and length L rotates on a friction less horizontal plane, with its centre of mass stationary. A particle of mass m is placed on the plane at a distance x=L3 from the centre of the stick . This stick hits the particle elastically
(a) Find the value of m so that after the collision, there is no rotational motion of the stick
(b) For what minimum of x can we get a value of ‘m’ so that the rod has no rotational motion after elastic collision ?
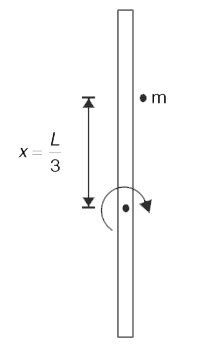 View Solution
View SolutionQuestion 133
A uniform rod of length L is rotating in a horizontal plane about a vertical axis passing through one of its ends. At a distance x(<L) from the axis there is a fixed vertical pole. The rod hits the pole and its direction of motion is reversed. Find x if it is known that during the impact the axis of rotation imparts no impulse to the rod. Does your answer depend on coefficient of restitution?
[NOTE : If you hit a lamp post with a rod, the hand holding the rod gets hurt as long as the impact misses the so called sweet spot of the rod (and hits either above or below the sweet spot). After solving the above problem you know where the sweet spot is ! You may assume that during the impact the rod is rotating about its holding hand. And if you play cricket, you know that there is a sweet spot in your bat too ! If the ball hits way above or below the spot you get stung.] View SolutionQuestion 134
Two identical thin rods are moving on a smooth table, as shown. Both of them are rotating with angular speed ω, in clockwise sense about their centres. Their centres have velocity V in opposite directions. The rods collide at their edge and stick together. Length of each rod is L.
(a) For what value of VωL there will be no motion after collision ?
(b) If the ratio VωL is half the value found in (a) above, what fraction of kinetic energy is lost in the collision?
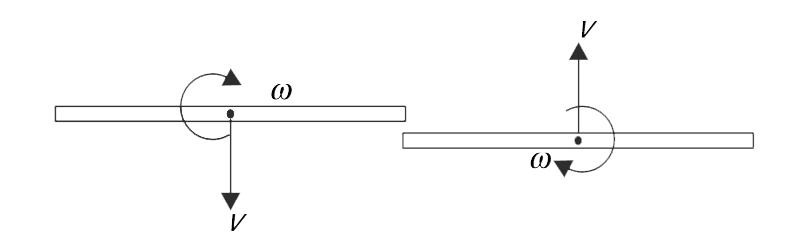 View Solution
View SolutionQuestion 135
Light thread is tightly wound on a uniform solid cylinder of radius R. The cylinder is placed on a smooth horizontal table and the thread is pulled horizontally as shown, by applying a constant force F. How much length of the thread is unwound from the cylinder by the time its kinetic energy becomes equal to K.
 View Solution
View SolutionQuestion 136
A horizontal disc of radius R and mas 20 M is pivoted to rotate freely about a vertical axis through its centre. A small insect A of mass M and another small insect B of mass mM4 are initially at diametrically opposite points on the periphery of the disc. The whole system is imparted an angular speed ω0 Insect A walks along the diameter with constant velocity v relative to the disc unit it reaches B which remains at rest on the disc. A then eats B and returns to its starting point along the original path with same speed v relative to the disc.
(a) Find the angular speed of the disc when A reaches the centre after eating B.
(b) Plot approximately, the variation of angular speed of the disc with time for the entire journey of the insect A. View SolutionQuestion 137
A disc of mass m and radius R is moving on a smooth horizontal surface with the flat circular face on the surface. It is spinning about its centre with angular peed ω and has a velocity V (see figure). It just manages to hit a stick AB at its end A. The stick was lying free on the surface and stick to the disc. [The combined object becomes like a badminton racket]. Mass and length of the stick are m and 2R respectively.
(a) Calculate the angular speed of the combined object assuming V=Rω
(b) Calculate loss in kinetic energy. Why is energy lost ?
(c) If V=η(Rω), loss in kinetic energy is minimum. Find η. (Assume ω is given]
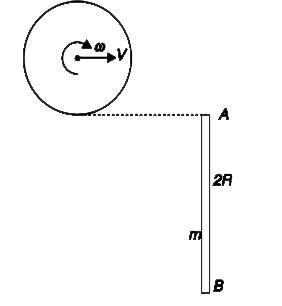 View Solution
View SolutionQuestion 138
A uniform rod of mass m and length l has been placed on a smooth table A particle of mass m, travelling perpendicular to the rod, hits it at a distance x=l√6 from the centre C of the rod. Collision is elastic.
(a) Find the speed of the centre of the rod and the particle after the collision.
(b) Do you think there is a chance of second Collision? If yes, how is the system of particle and stick moving after the second collision?
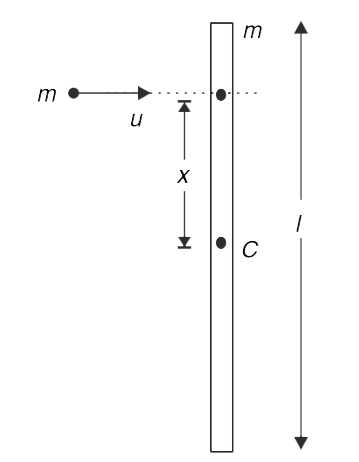 View Solution
View SolutionQuestion 139
A ring is made to rotate about its diameter at a constant angular speed of ω0 . A small insect of mass m walks along the ring with a uniform angular speed ω relative to the ring (see figure). Radius of the ring is R.
(a) Find the external torque needed to keep the ring rotating at constant speed as the insect walks. Express your answer as a function of θ. For what value of q is this torque maximum? [given your answer for 0≤θ≤90∘ ]
(b) Find the component of force perpendicular to the plane of the ring, that is applied by the ring on the insect. For what value of θ is this force maximum? Argue quantitatively to show that indeed the force should be maximum for this value of θ. [Give your answer for 0∘≤θ≤90∘ ]
 View Solution
View SolutionQuestion 140
A small car took off a ramp at a speed of 30m/s. Immediately after leaving the ramp, the driver applied brakes on all the wheels. The brakes retarded the wheels uniformly to bring them to rest in 2 second. Calculate the angle by which the car will rotate about its centre of mass in the 2 second interval after leaving the ramp. Radius of each wheel is r=0.30m . Moment of inertia of the car along with the driver, about the relevant axis through its centre of mass is IM=80kgm2 and the moment of inertia of each pair of wheels about their respective axles is 0.3kgm2. Assume that the car remained in air for more than 2 second . Also assume that before take- off the wheels rolled without sliding.
 View Solution
View SolutionQuestion 141
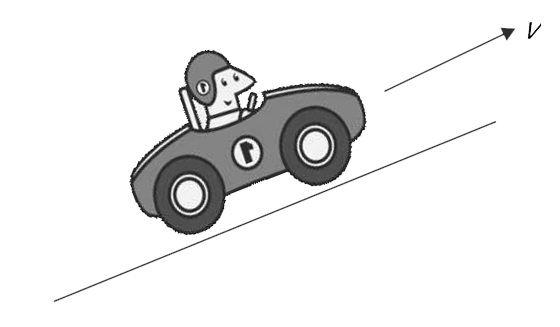
A disc of radius R stands at the edge of a table. If the given a gentle push and it beings to fall. Assume that the disc does not slip at A and it rotates about the point as it falls. The falling disc hits the edge of another table placed at same height as the first one at a horizontal distance of √2R. Imagine that the disc hits the edge B and rotates (up) about the edge
(a) Find the speed of the centre of the disc at the instant just before it hits the edge B.
(b) Find the angular speed of the disc about B just after the hit.
 View Solution
View SolutionQuestion 143
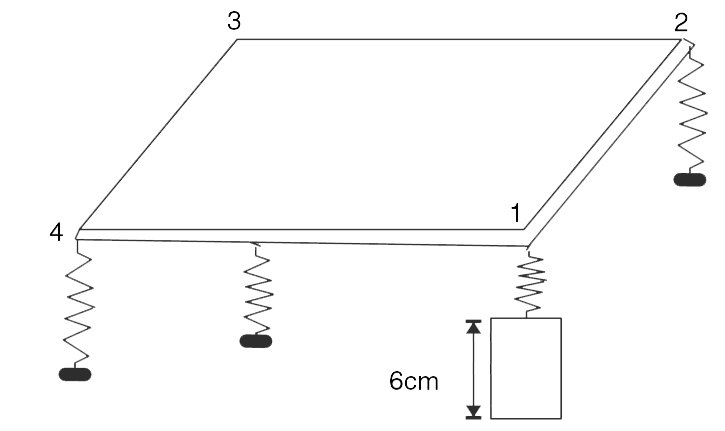
A rigid large uniform square platform is resting on a flat horizontal ground supported at its vertices by four identical spring. At vertex l a wooden block, 6 cm high, is inserted below the spring. Calculate the change in height of the centre of the platform. Assume change in height to be small compared to dimension of the platform.
 View Solution
View SolutionQuestion 144
A uniform rod of mass M and length L is placed freely on a horizontal table. A horizontal force F is applied perpendicular to the rod at one of its ends. The force F is increased gradually from zero and it is observed that when its value becomes F0, the rod just begins to rotate about point O
(i) Find length AO
(ii) Find F0
 View Solution
View SolutionQuestion 145
A ring of mass M and radius R lies flat on a horizontal table. A light thread is wound around it and its free end is pulled with a constant velocity v.
(a) Two small segment A and B (see fig.) in the ring are rough and have a coefficient of friction μ with the table. Rest of the ring is smooth. Find the speed with which the ring moves.
(b) Find the speed of the ring if coefficient of friction is μ everywhere, for all points on the ring.
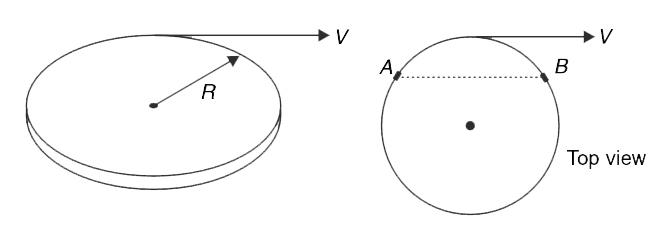 View Solution
View SolutionQuestion 146
A uniform stick of length L is pivoted at one end on a horizontal table. The stick is held forming an angle θ0 with the table. A small block of mass m is placed at the other end of the stick and it remains at rest. The system is released from rest
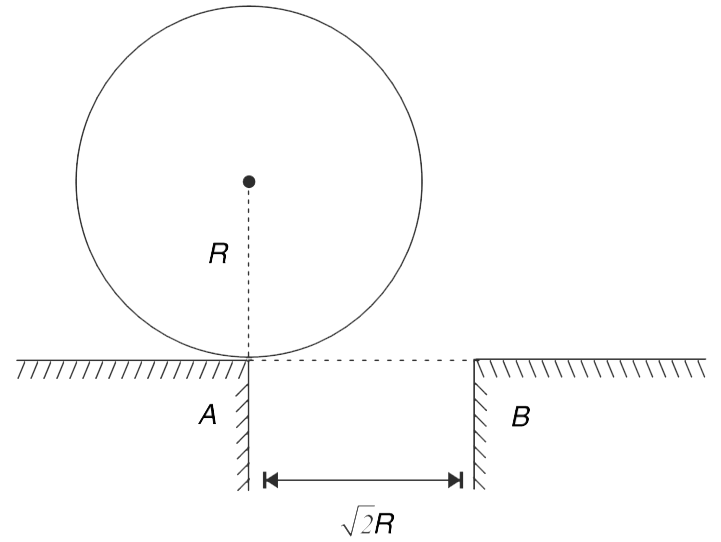
(a) Prove that the stick will hit the table before the block if cosθ0≥√23
(b) Find the contact force between the block and the stick immediately before the system is released.Take θ0=cos−1(√23)
(c) Find the contact force between the block and the stick immediately after the system is released if θ0cos−1(√23).
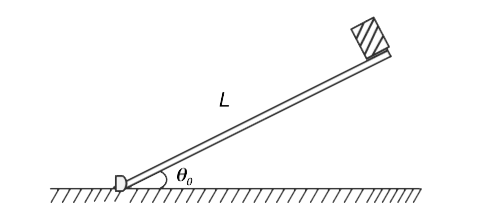 View Solution
View SolutionQuestion 147
A uniform rod BC with length a is attached to a light string AC. End A of the string is fixed to the ceiling and the end B of the rod is on a smooth horizontal surface. B is exactly below point A and length AB is b(a<b<2a). The system is released from rest and the rod begins to slide. Find the speed of the centre of the rod when the string becomes vertical.
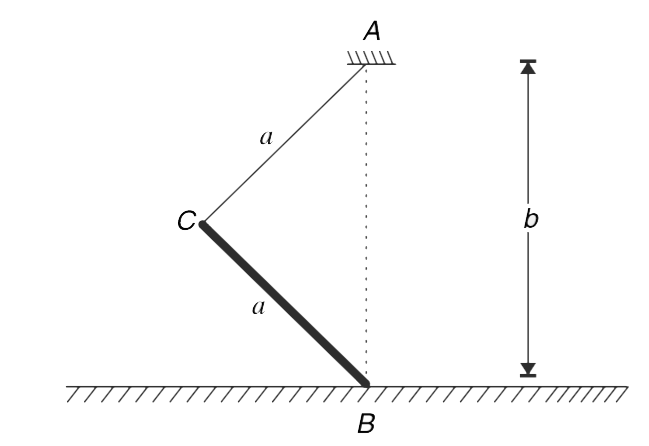 View Solution
View SolutionQuestion 148
A dumb – bell has a rigid mass less stick and two point masses at its ends. Each mass is m and length of the stick is L. The dumb- bell leans against a frictionless wall, standing on a frictionless ground. It is initially held motionless, with its bottom end an infinitesimal distance from the wall. It is released from this position and its bottom end slides away from the wall where as the top end slides down along the wall.
(a) Show that centre of mass of the dumb-bell moves along a circle.
(b) When the dumb-bell loses contact with the wall what is speed of the centre of mass?
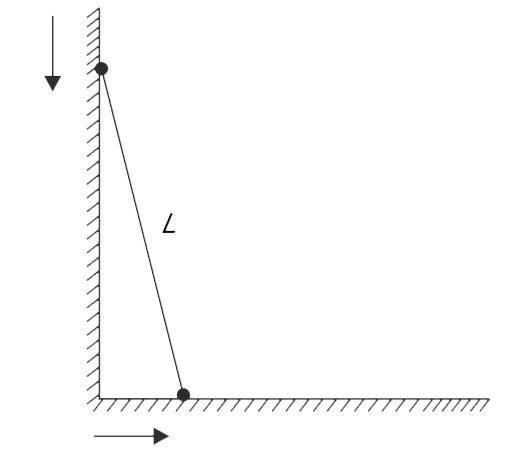 View Solution
View SolutionQuestion 149
A hexagonal pencil of mass M and sides length a has been placed on a rough incline having inclination θ Friction is large enough to prevent sliding. If at all the pencil moves, during one full rotation each of its 6 edges, in turn, serve as instantaneous axis of rotation.
(a) Show that for θ>30∘ the pencil cannot remain at rest.
(b) For inclination of incline θ<30∘ the pencil will not roll on its own. A sharp impulse J is given to the pencil parallel to the incline at its upper edge (see figure). Friction does not allow the pencil to slide but it begins to rotate about the edge through A with initial angular speed ω0. Find ω0. Moment of inertia of the pencil about its edge is I.
(c) Find minimum value of J so that the pencil will turn about A, and B will land on the incline.
(d) If kinetic energy acquired by the pencil just after the impulse is K0, find its kinetic energy just before edge B lands on the incline
 View Solution
View SolutionQuestion 150
A rope of length L and mass per unit length λ passes over a disc shaped pulley of mass M and radius R. The rope hangs on both sides of the pulley and the length of larger hanging part is l. The pulley can rotate about a horizontal axis passing through its centre. The system is released from rest and it begins to move. The pulley has no friction at its axle and the rope has large enough friction to prevent it from slipping on the pulley.
(a) Find the acceleration of the rope immediately after it is released.
(b) Find the horizontal component of the force applied by the axle on the pulley immediately after the system is released
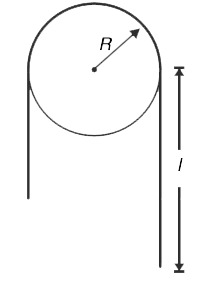 View Solution
View SolutionQuestion 151
A toy is made of a rectangular wooden frame with four small wheels at its vertices. A tight fitting belt of negligible mass runs around the frame passing over the wheels. Mass of the complete toy is M. Now a small block of mass m is stuck at the top of the right vertical segment of the belt and the system is released. Height of the toy is h. Find the speed of the block when it is about to hit the ground. Assume no slipping anywhere and neglect the dimension of the wheels
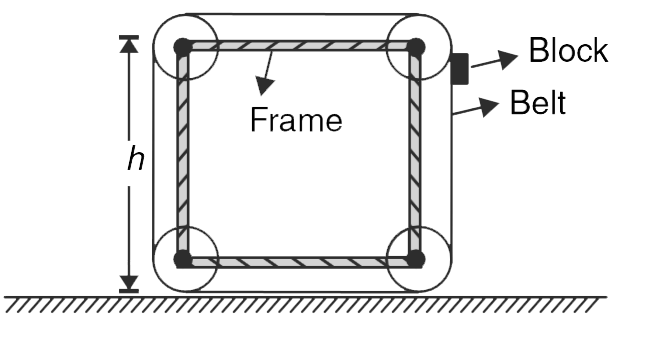 View Solution
View SolutionQuestion 152
Consider an idealized case of rolling of a solid ball in which the point P does not rotate in a vertical plane. But it rotates on circular path PQRSTP when observed from the centre of the ball. The radius of circular path PQRSTP is half the radius of the ball. The ball rolls without sliding with its centre moving with speed v0 in direction perpendicular to the plane of the figure calculate the kinetic energy of the rolling ball. Mass of the ball and its radius are M and R respectively.
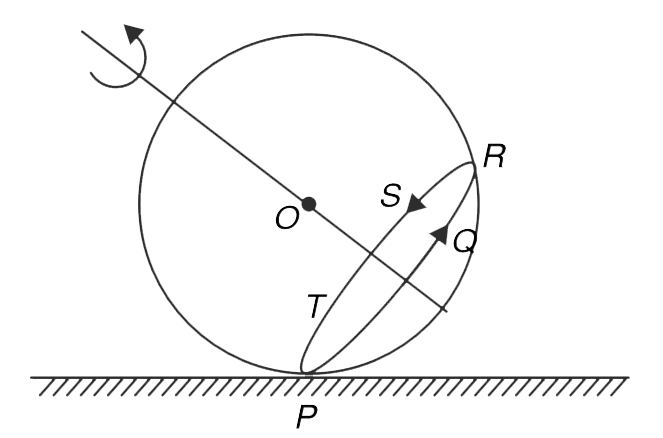 View Solution
View SolutionQuestion 153
Two identical rings, each of mass M and radius R, are standing on a rough horizontal surface. The rings overlap such that the horizontal line passing through their centre makes an angle of θ=45∘ with the radius through their intersection point P. A small object of mass m is placed symmetrically on the rings at point P and released. Calculate the acceleration of the centre of the ring immediately after the release. There is no friction between the small object and the rings. The friction between the small object and the rings, and the friction between the rings and the ground is large enough to prevent slipping.
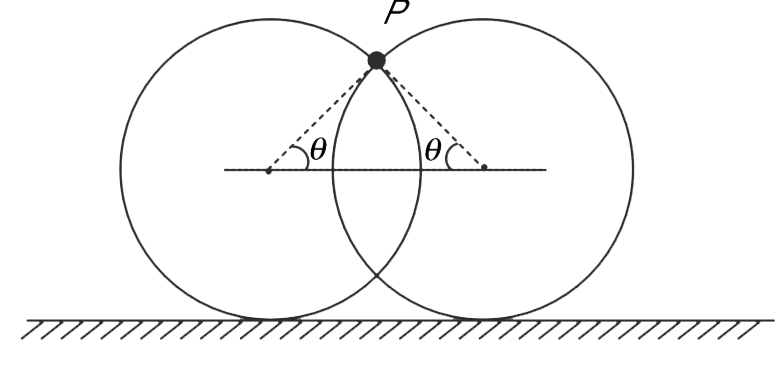 View Solution
View SolutionQuestion 154
A uniform rope tightly wraps around a uniform thin ring the mass M and radius R. The mass of the segment of the rope around the ring (i.e. , mass of the length2πR of the rope) is also M. The ends of the rope are fixed one above the other and it is taut. The ring is let go. Find its acceleration. Assume no slipping and thickness of the rope to be negligible.
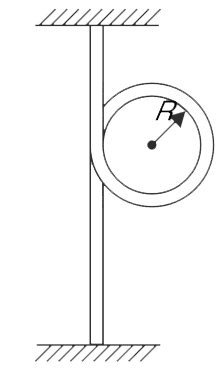 View Solution
View SolutionQuestion 155
A uniform stick AB has length L. It is tossed up from horizontal position such that its centre receives a velocity uπ√gL in vertically upward direction and the stick gets an angular velocity. The stick lands back to its point of projection in horizontal position. During its course of flight its angular velocity remained constant and the stick made one complete rotation. Stick rotates in vertical plane.
(a) Calculate the angular velocity (ω) imparted to the stick.
(b) Calculate the maximum height, above the point of projection, to which the end B of the stick rises.
[Take solution of equation cosx=2x to be x=0.45 and sin(0.45)=0.43]
 View Solution
View SolutionQuestion 156
A uniform rod of mass 4m and length 2r can rotate in horizontal plane about a vertical axis passing through its centre O. Two small balls each of mass m are attached to its ends. A fixed gun fires identical balls with speed v in horizontal direction. The firing is being done at suitable intervals so that the fired balls either hit the ball at end A or B while moving in the direction of velocity of A or B. All collisions are elastic.
(i) Initial angular velocity of the rod is zero and its angular velocity after nth collision is ωn Write ωn+1 in terms of ωn
(ii) Solve the above equation to get ωn<br>(iii)F∈dthelimit∈gvalueofomega.
 View Solution
View SolutionQuestion 157
A uniform rod of mass m and length 2L on a smooth horizontal surface. A particle of mass m is connected to a string of length L whose other end is connected to the end ‘A’ of the rod. Initially the string is held taut perpendicular to the rod and the particle is given a velocity v0 parallel to the initial position of the rod.
(a) Calculate the acceleration of the centre of the rod immediately after the particle is projected.
(b) The particle strikes the centre of the rod and sticks to it. Calculate the angular speed of the rod after this.
 View Solution
View SolutionQuestion 158
Two boys support by the ends a uniform rod of mass M and length 2L. The rod is horizontal. The two boys decided to change the ends of the rod by throwing the rod into air and catching it. The boys do not move from their position and the rod remained horizontal throughout its flight. Find the minimum impulse applied by each boy on the rod when it was thrown View SolutionQuestion 159
A uniform rod of mass m and length l pivoted at one of its top end is hanging freely in vertical plane. Another identical rod moving horizontally with velocity v along a line passing through its lower end hits it and sticks to it. The two rods were perpendicular during the hit and later also they remain perpendicularly connected to each other. Find the maximum angle turned by the two-rod system after collision.View Solution