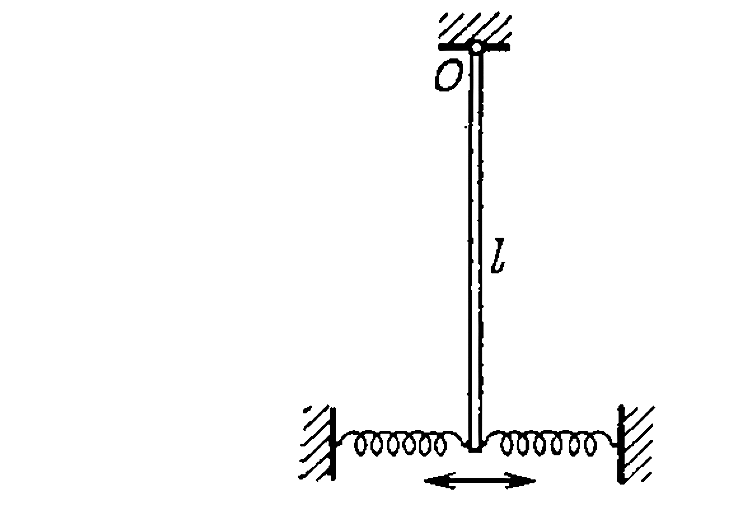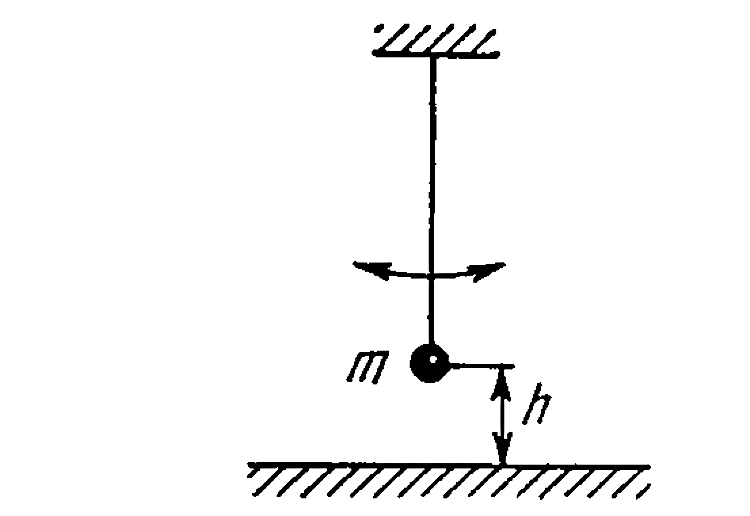Electromagnetic Waves, Radiation from IE IRODOV PHYSICS (HINGLISH) OSCILLATIONS AND WAVES for Class 12
| Class 12 | PHYSICS |
| Chapter | OSCILLATIONS AND WAVES |
| IE IRODOV PHYSICS (HINGLISH) | Electromagnetic Waves, Radiation |
| Medium | English |
| Academic Year | 2023-2024 |
Question 1
A point oscillates along the x axis according to the law x=acos(ωt−π/4). Draw the approximate plots
(a) of displacemetn x, velocity projection υx, and acceleration projection wx as functions of time t,
(b) velocity projection υx and acceleration projection wx as functions of the coordiniate x. View SolutionQuestion 3
A particle performs harmonic oscillations along the x axis about the equilibrium position x=0. The oscillation frequency is ω=4.00s−1. At a certain moment of time the particle has a coordinatex0=25.0cm and its velocity is equal to vx0=100cm/s.
Find the coordinate x and the velocity vx of the particle t=2.40s after that moment. View SolutionQuestion 5
A point performs harmonic oscillations along a straight line with a period T=0.60s and amplitude a=10.0cm. Find the mean velocity of the point averaged over the time interval during which it travels a distance z/2, starting from
(a) the extreme position.
(b) the equilibrium position. View SolutionQuestion 6
At the moment t=0 a point starts oscillating along the x axis according to the laswx=asinωtt. Find:
(a) the mean value of its velocity vector projection (:vx:),
(b) the modulus of the mean velocity vector |(:v:)|,
(c) the mean value of the velocity modulus (:v:) averaged over 3/8 of the period after the start.View SolutionQuestion 9
A particle performs harmonic oscillations along the x axis according to the lawx=acosωt. Assuming the probablity P of the particle to fall withing an interval from −a to +a to be equal to unity, find how the probability density dP/dx depends on x. Here dP denotes the probablitity of the particle falling within an interval frm x to x+dx. Plot dP/dx as a function of x. View SolutionQuestion 12
The superposition of two harmonic oscillations of the same direction results in the oscillation of a point according to the law x=acos2.1tcos50.0t, where t is expressed in seconds. Find the angular frequencies of the constituent oscillations and the period with which they beat. View SolutionQuestion 13
A point A oscillates according to a certain harmonic law in the reference frame K′ which in its turn performs harmonic oscillations relative to the reference fromeK. Both oscillations occur along the same direction. When the K′ frame oscillates at the frequency 20 or 24Hz, the beat frequency of the point A in the K frame turns out to be equal to v. At what frequency of oscillation of the frame K′ will the beat frequency of the point A become equal to 2v?View SolutionQuestion 14
A point moves in the plane xy according to the law x=asinωt,y=bcosωt, where a,b and ω are positive constants.
Find :
(a) the trajectory equation y(x) of the point and the direction of its motion along this trajectory ,
(b) the acceleration w of the point as a function of its radius vector r relative to the orgin of coordinates.View SolutionQuestion 20
A ball is suspended by a thread of length l at the point O on an incline wall as shown. The inclination of the wall with the vertical is α.The thread is displaced through a small angle β away from the vertical and the ball is released. Find the period of oscillation of pendulum.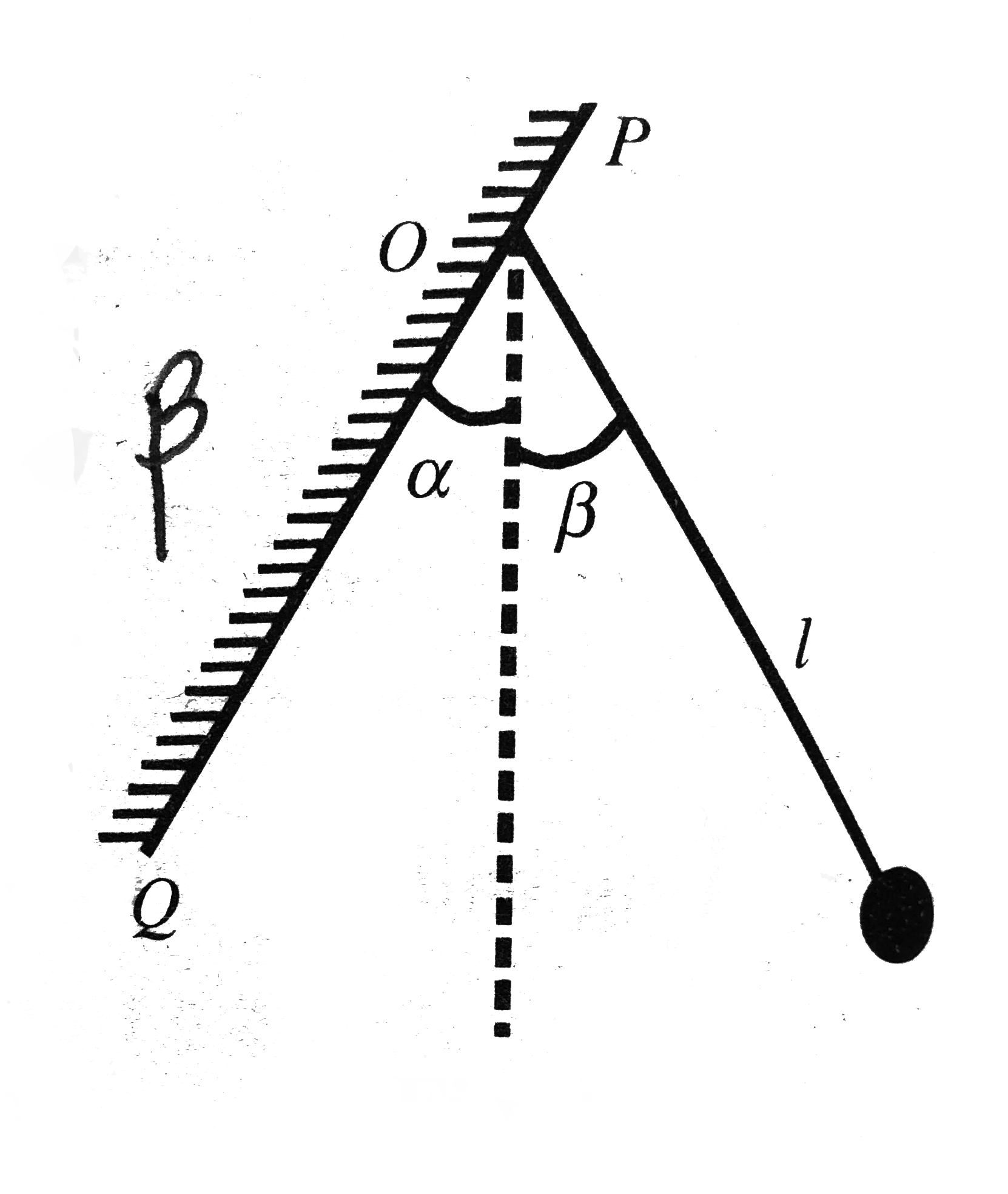
Consider both cases
a. α>β
b. α<β
Assuming that any impact between the wall and the ball is elastic.View SolutionQuestion 21
A pendulum clock is mounted in an elevator car which starts goint up with a constant acceleration w, with w<g. At a height h the acceleration of the car reverses, its magnitude remaining constant. How soon after the start of the motion will the clock show the right time again ?View SolutionQuestion 22
Calculate th eperiod of small oscillations of a hydrometer which was slightly pushed down in the vertical direction. The mass of the hydrometer is m=50g, the radius of its tube is r=3.2mm, the density of the liquuid is ρ=1.00g/cm3 . The rsistance of the liquid is assumed to be negligible.
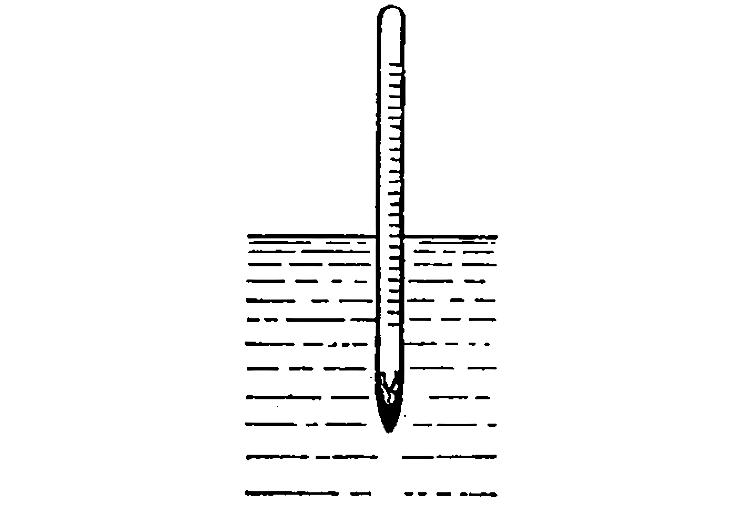 View Solution
View SolutionQuestion 23
A non-deformed spring whose ends are fixed has a stiffness x=13N/m. A small body of mass m=25g is attached at the point removed from one of the ends by η=1/3 of the spring's length. Neglecting the mass of the spring, find the period of small longitudinal oscillations of the body. The force of gravity is assumed to be absent.
View SolutionQuestion 26
A small body of mass m is fixed to the middle of a stretched string of length 2l. In the equlibrium position the string tension is equal to T0. Find the angular freqency of small oscillations of the body in the transverse direction. The mass of the string is negligible, the gravitational field is absent.
View SolutionQuestion 29
Imagine a shaft going all the way through the Earth from pole to pole along its rotation axis. Assuming the Earth to be a homogenous ball and neglecting the ari drag, find :
(a) the equation of motion of a body falling down into the shaft ,
(b) how long does it take the body to reach the other end of the shaft,
(c) the velocity of the body at the Earth's centre. View SolutionQuestion 30
Find the period of small oscillations of a mathematical pendulum of length l if its point of suspension O moves relative to the Earth's surface in an arbitrary directio with a constant acceleration w (figure). Calculate that period if l=21cm,w=g/2, and the angle between the vectors w and g equals beat=120∘.
 View Solution
View SolutionQuestion 31
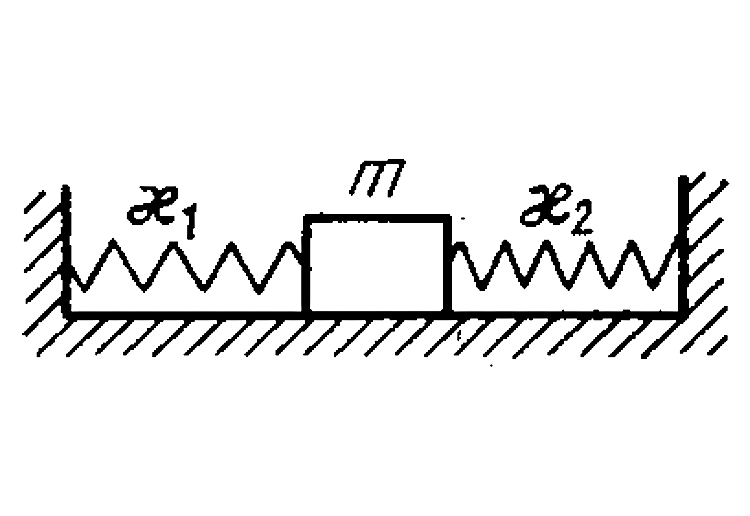
In the arrangement shown in figure the sleeve M of mass m=0.20kg is fixed between two identical springs whose combined stiffness is equal to x=20N/m. The sleeve can slide without friction over a horizontal bar AB. The arrrangement rotates with a constant angular velocity ω=4.4rad/s about a vertical axis passing through the middle of the bar . Find the period of small oscillations of the sleeve. At what values of ω will there be no oscillations of the sleeve ?
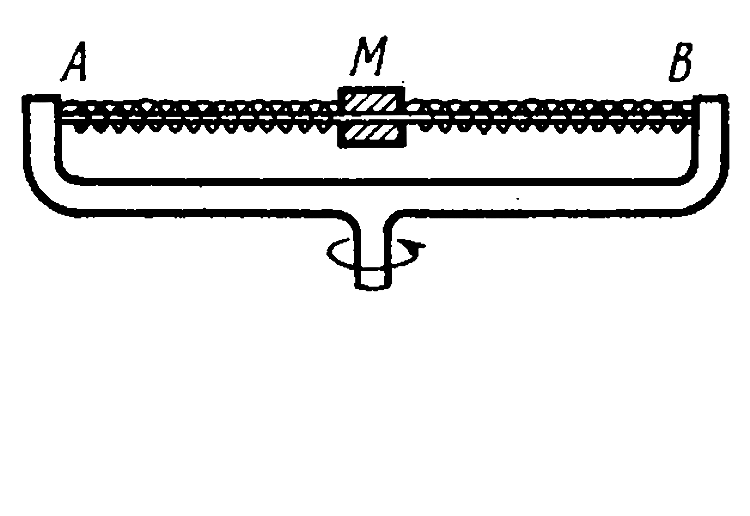 View Solution
View SolutionQuestion 32
A plank with a bar placed on it performs horizontal harmonic oscillations with amplitude a=10cm. Find the coefficient of friction between the bar and the plank if the former starts sliding along the plank when the amplitude of oscillation of the plank becomes less than T=1.0s. View SolutionQuestion 33
Find the time dependece of the angle of deviation of a mathematical pendulum 80cm in length if at the initial moment the pendulum.
(a) was deviated through the angle 3.0 and then set free without push,
(b) was in the equlibrium position and its lower end was imparted the horizontal velcoity 0.22m/s,
(c ) was deviated throught the angle 30∘ and its lower end was imparted the velocity 0.22m/s derected toward the equilibrium position. View SolutionQuestion 34
A body A of mass m1=1kg and a body B of mass m2=4kg are attached to the ends of a spring. The body A performs vertical simple harmonic oscillations of amplitude a=1.6cm and angular frequencyω=25rads. Neglecting the mass of the spring determine the maximum and minimum values of force the system exerts on the surface on which in rests.
[Take g=10m/s2]
 View Solution
View SolutionQuestion 35
A plank with a body of mass m places on it starts moving straight up according to the law y=a(1−cosωtt), whee y is the displacement from the initial position, ω=11s−1. Find :
(a) the time dependence of the force that the body exerts on the plank if a=4.0cm, plot this dependence,
(b) the minimum amplitude of oscillation of the plank atwhich the body starts falling behind the plank,
(c) the amplitude of oscillation of the plank at which the body springs up to a height h=50cm relative to the initial position (at the moment t=0). View SolutionQuestion 36
A body of mass m was suspended by a non-stretched spring, and then set fre without push. The stiffness of the spring is x. Neglecting the mass of the spring , find :
(a) the law of motion y(t), whee y is displacement of the body from the equilibrium position,
(b) the maximum and minimum tensions of the spring in the process of motion. View SolutionQuestion 37
A particle of mass m moves due to the force F=−αmr, where α is a positve constant ,r is the radius vector of the particle relative to the origin of coordinates. Find the trajectory of its motion if at the initial moment r=r0i and the velocity v=υ0j, whee i and j are the unit vectors of the x and y axes. View SolutionQuestion 38
A body of mass m is suspended from a spring fixed to the ceiling of an elevator car. The stiffness of the spring is x. At the moment t=0 the car starts going up with an accelerationw. Neglecting the mass of the spring , find the law of motion y(t0 of the body relative to the elevator car if y(0)−0 and y(0)=0. Consider the following two cases :
(a) w=const,
(b) w=αt, where αis a constant. View SolutionQuestion 42
A particle of mass m moves in pane xy due to the force varying with velocity as F=a(.y−.xj), where a is a positve constant, i and j are the unit vectors of the x and y axes. At the initial momentt=0 the particle was located at the point x=y=0 and possessed a velocity v0 directed along the unit vector j. Find the law of motino x(t),y(t) of the particle, and also the equation of its trajectory.View SolutionQuestion 43
A pendulum is constructed as a light thin− walled sphere of radius R filled up with water and suspended at the point O from a light rigid rod (figure). The distance between the point O and the centre of the sphere is equal to l. How many times will the small oscillations of such a pendulum change after the water freezes ? The visxosity of water and the change of its volume on freezes? The viscosity of water and the change of its volume on freezing are to be necglected.
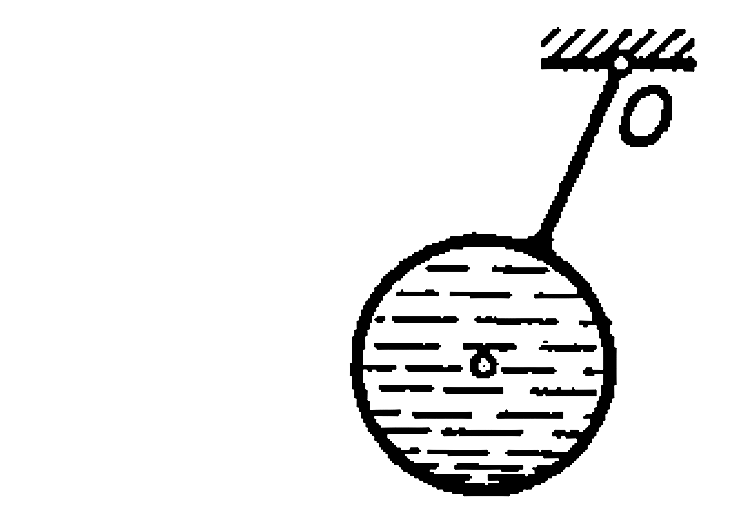 View Solution
View SolutionQuestion 45
A uniform rod of mass m=1.5kg suspended by two identical threads l=90cm in length ( figure ) was turned through a small angle about the vertical axis passing through its middle point C. The threads deviated in the process through an angle α=5.0∘. Then the rod was released to start performing small oscillations.
Find:
(a) the oscillation period,
(b) the rod's oscillation energy.
 View Solution
View SolutionQuestion 46
An arrangedment illlustrated in figure consists of a horizontal uniform disc D of mass m and radius R and a thin rod AO whose torsional coefficient is equal to k. Find the amplitude and the energy of small torsional oscillationa if at the initial momentu the disc was deviated through an angle φ0 from the equilibrium position and then imparted an angular velocity φ0.
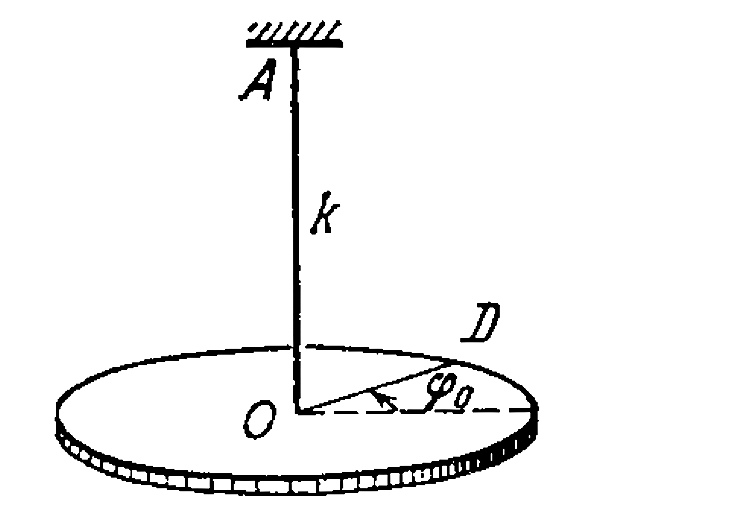 View Solution
View SolutionQuestion 47
A uniform rod of mass m and length l performs small oscillations about the horizontal axis passing throughits upper end. Final the mean kinetic energy of the rod averaged over one oscillation period it at the initial mment it was deflected from the vertical by an angle θ0 and then imparted an angular velocity θ0. View SolutionQuestion 49
A physical pendulum performs small oscillations about the horizontal axis with frequency ω1=15.0s−1. When a small body of mass m=50g is fixed to the pendulum at a distance l=20cm below the axis, the oscillation frequency becomes equal to ω2=10.0s−1. Find the moment of inertia of the pendulum relative to the oscillation axis. View SolutionQuestion 50
Two physical pendulums perform small oscillations about the same horizontal axis with frequencies ω1 and ω2 . Their moments of inertia relative to the given axis are equal to I1 and I2 respectively. In a state of stable equilibium the pendulums were fastened rigifly together. What will be the frequency of small oscillations of the compound pendulum ?View SolutionQuestion 51
A uniform rod of length l performs small oscillations about the horizontal axis OO′ perpendicular to the rod and passing through one of its points. Find the distance the centre of inertia of the rod and the axis OO′ at which the oscillation period is the shortest. What is it equal to ?View SolutionQuestion 53
A smooth horizontal disc rotates about the vertical axis O (figure) with a constant angular velocity ω. A thin uniform rod AB of length l performs small oscillation about the vertical axis A fixed to the disc at a distance a from the axis of the disc. Find the frequency ω0 of these oscillations.
 View Solution
View SolutionQuestion 54
Find the frequency of small oscillations of the arrangement illustrated in figure. The radius of the pulley is R, its moment of inertia relative to the rotation axis is I, the mass of the body is m, and the spring stiffness is x.The mass of the thread and the spring is negligible , the thread does not slide over the pulley, there is no friction in the axis of the pulley
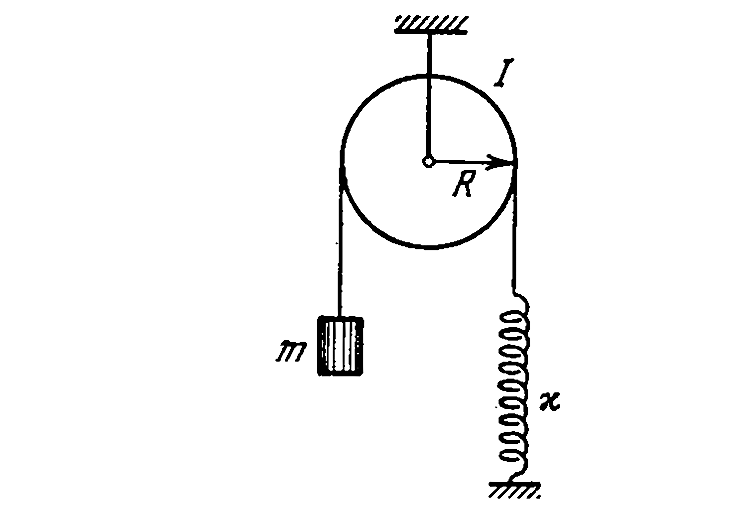 View Solution
View SolutionQuestion 55
A uniform cylindrical pulley of mass M and the radius R can freely rotate about the horizontal axis O (figure). The free end of a thread tightly wound on the pulley carries a deadweight A. At a certain angle α it counterbalanes a point mass m fixed at the rim of the pulley. Find the frequency of small osicllations of the arrangement.
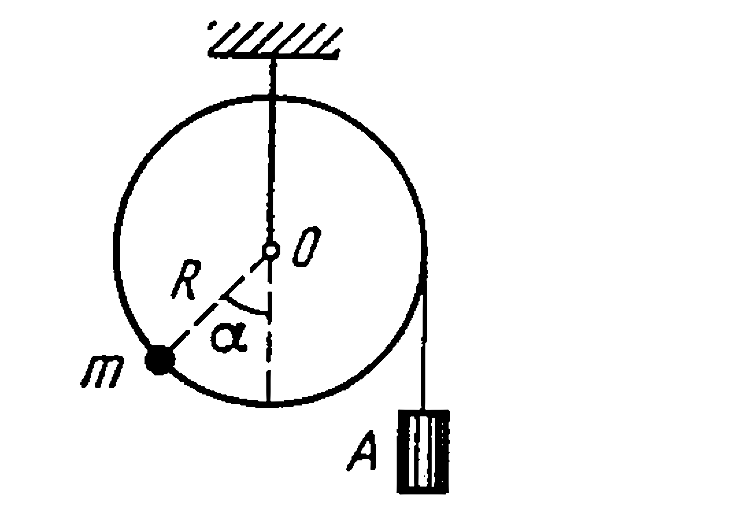 View Solution
View SolutionQuestion 59
Two balls with massesm1=1.0kg and m2=2.0kg are slipped on a thin smooth horizontal rod ( figure). The balls are interconnected by a light spring of stiffness x=24N/m. The left- hand ball is imparted the initial velocity v1=12cm/s. Find :
(a) the oscillation frequency of the system in the process of motion,
(b) the energy and the amplitude of oscillations
 View Solution
View SolutionQuestion 61
A mock− up of a CO2 molecule consists of three balls interconnected by identical light springs and placed along a straight line in the state of equilibrium. Such a system can freely perform oscillation of two types, as shown by the arrows in figure. Knowing the masses of the atomes, find the ration of frequencies of these oscillations
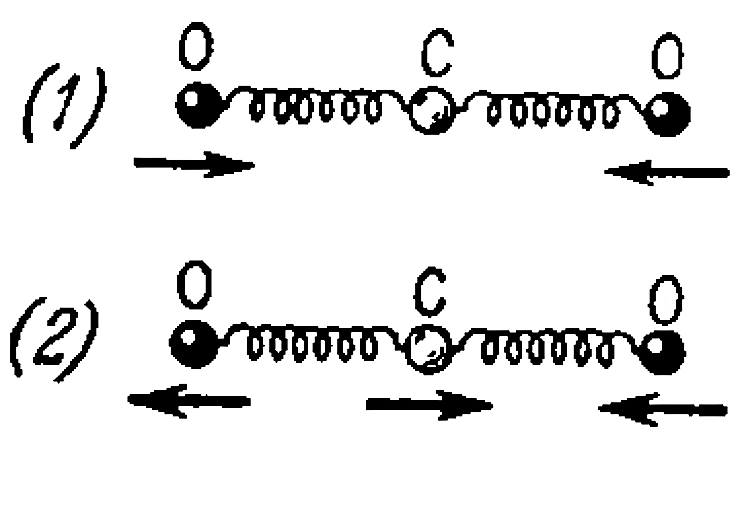 View Solution
View SolutionQuestion 62
In a cylinder filled up with ideal gas end gas and closed from both ends there is a piston of mass m and cross − sectional area S (figure).In equilibrium the piston divides the cylinder into two equal parts, each with volime V0 . The gas ppressure is p0. The piston was slightly displaced from the equlibrium position and released.Find the oscillation frequency, assuming the prosecces in the gas to be adiabatic and the friction negligible.
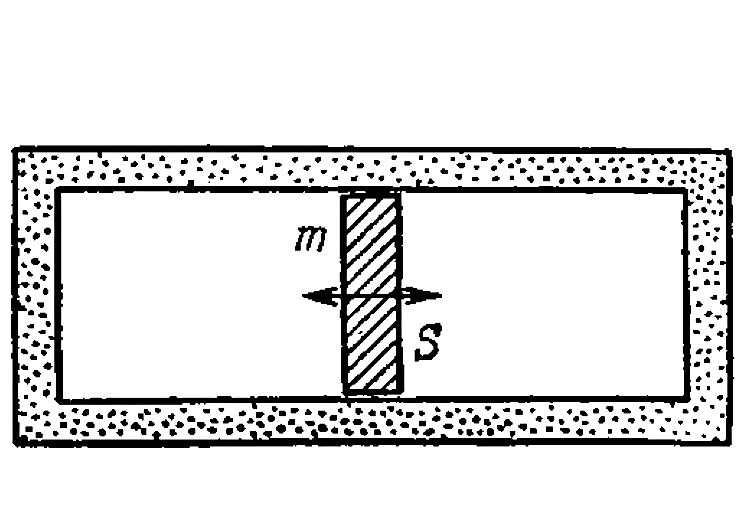 View Solution
View SolutionQuestion 64
A small magnetic needle performs small oscillations about an axis perpendicular to the magnetic induction vector. On changing the magnetic induction the neddle's oscillation period decreases η=5.0 times. How much and in what way was the magnetic induction changed ? The oscillation damping is assumed to be negligible. View SolutionQuestion 65
A loop (figure) is formed by two parallel conductores connected by a solenoid with inductance L and a conducting rod of mass m which can freely ( without friction) slide over the conductors. The conductors are located in a horizontal plane in a uniform vertical magnetic field with induction B. The distance between the conductors is equal to l. At the moment t=0 the rod is imparted an initial velocity υ0 directed to the right. Find the law of its motion x(t) if the electric resistance of the loop is negligible.
 View Solution
View SolutionQuestion 66
A coil of inductance L connects the upper ends of two vertical copper bars separated by a distance l . A horizontal conducting connnector of mass m starts falling with zero initial velocit along the bars without losing contact with them. The whole system is located in a uniform magnetic field with induction B perpendicular to the plane of the bars. Find the law of motion x(t) of the connector. View SolutionQuestion 69
A point performs damped oscillations with frequency ω and damping coefficient β according to the (4.1b). Find the initial amplitude a0 and the initial phase α if at the moment t=0 the displacement of the point and its velocity projection are equal to
(a) x(0)=0 and ux(0)=.x0 ,
(b) x(0)=x0 and vx(0)=0.View SolutionQuestion 71
A point performs damped oscilaltions with frequency ω and dampled coefficient β. Find the velocity amplitude of the point as a function of time t if at the moment t=0
(a) its displacement amplitude is equal to a0,
(b) the displacement of the point x(0)=0 and its velocity projection vx(0)=.x0View SolutionQuestion 73
A mathematical pendulum oscillates in a medium for which the logarithmic damping decrement is equal to λ0=1.50. What will be the logarithmic damping decrement if the resistance of the medium increases n=2.00 time? How many times has the resistance of the medium to be increased for the oscillations to become impossible?View SolutionQuestion 79
A thin uniform disc of mass m and radius R suspended by an elastic thread in the horizontal plane performs torsional oscillations in a liquid. The moment of leastic forces emerging in the thread is equal to N=αφ, where α is a constant and φ is the angle of rotation from the equilibrium position. The resistance force acting on a unit area of the disc is equal to F1ηv, whereη is a constant and v is the velocity of the given element of the disc relative to the liquid. Find the frequency of small oscillation. View SolutionQuestion 80
A disc A of radius R suspended by an elastic threat between two stationary plane ( figure ) performs torsional oscillations about its axis OO′ . The moment of inertia of the disc relative to that axis is equal to I, the clearance between the disc and each of the planes is equal to h, with h<<R. Find the viscosity of the gas surrounding the disc A if the oscilaltion period of the disc equals T and the logarithmic damping decrement, λ.
 View Solution
View SolutionQuestion 81
A conductor is the shape of a square frame with side a suspended by an elastice thread is located in a uniform horizontal magnetic field with induction B. In equuilibrium the plane of the fame is parallel to the vector B (figure). Having been displaced from the equilibrium position, the frame performs small oscillation about a vertical axis passing through its centre. The moment of inertia of the grame relative to that axis is equal to I, it electric resistance is R. Neglecting the inductance of the frame, find the time interval after which the amplitude of the frame's deviation angle decreases e− fold.
 View Solution
View SolutionQuestion 82
A bar of mass m=0.50kg lying on a horizontal plane with a friction coefficient k=0.10 is attached to the wall by means of a horizontal non− deformed spring. The stiffness of the spring is equal to x=2.45N/cm, its mass is negligibl . The bar was displaced so that the spring was stretched by x0=3.0cm, and then released. Find :
(a) the period of oscillation of the bar ,
(b) the total number os osciallations that the bar performs untial it stops completely. View SolutionQuestion 83
A ball of mass m can perform undamped harmonic oscillations about the point x=0 with natural frquency, ω0. At the moment t=0, when the ball was in equilibrium, a force Fx=F0cosωt coinciding with the x axis was applied to it. Find the law of forced oscillation x(t) for that ball. View SolutionQuestion 84
A particle of mass m can perform undamped harmonic oscillations due to an electric force with coefficient k. When the particle was in equilibrium, a permanent force F was applid to to its for τ seconds. Find the oscillation amplitude that the particle acquired after the action of the force ceased. Draw the approximate plot x(t) of oscillations. Investigate possible cases. View SolutionQuestion 85
A ball of mass m when suspended by a spring stretches the latter by Δl. Due to external vertical lforce varying according to a harmonic law with amplitude F0 the ball performs forced oscillations. The logarighmic damping decrement if equal to λ. Neglecting the mass the spring, find the angular frequency of the external force at which the displacemetn amplitude of the ball is maximum. What is the magnitude of that amplitude ?View SolutionQuestion 87
The velocity amplitude of a particle is equal to half the maximum value at the frequencies ω1 and ω2 of external harmonic force.
Find:
(a) the frequency corresponding to the velocity resonance,
(b) the damping coefficient β an dthe damped oscillation frequency ω of the particle. View SolutionQuestion 90
A ball of mass m=50g is suspended by a weightless spring with stiffness x=20.0N/m. Due to external vertical harmonic force with frequency ω=25.0s−1 the ball performs steady − state oscillations with amplitude a=1.3cm. In this case the displacement of the ball lags in phase behind the external force by φ=34π. Find :
(a) the quality factor of the given oscillator ,
(b) the work performed by the external force during one oscillation period. View SolutionQuestion 91
A ball of mass m suspended by a weightless spring can perform vertical oscillations with damping coefficient β. The natural oscillation frequency is equal to ω0. Due to the external vertical force varying as F=F0cosωt the ball performs steady − state harmonic oscillations. Find :
(a) the mean power (:P:) , develocped by the force F. averaged over one oscillations perod,
(b) the frequency ω of the force F at which (:P:) is maximum, what is (:P:)max equal to ?View SolutionQuestion 92
An external harmonic force F whose frequency can be varied, with amplitude maintained constant, acts in a vertical direction on a ball suspended by a weightless spring. The damping coefficient is η times less than the natural oscillation frequency ω0 of the ball. How much, in per cent, does the mean power (:P:) developed differ from the maximum mean power (:P:)max? Averaging is performed over one oscillation period. View SolutionQuestion 93
A uniform horizontal disc fixed at its centre to an elastic vertical rod performs forced torsional oscillations dur to the moment of forces Nz=Nmcosωt. The oscialltions obey the law φ=φmcos(ωt−α).
(a) the work performed by friction forces acting on the disc during one oscillation period ,
(b) the quality factor of the given oscillator if th emoment of inertia of the disc relative to the axis is equal to I. View SolutionQuestion 94
If the elctron ( charge of each electron =−e) are shifted by a small distance x,a net +ve charge density ( per unit area ) is induced on the surface. This will result in an electric field E=nex/ε0 in the direction of x and a restoring force on an electron of
−ne2xε0,
Thus m..x=−ne2xε0
or ..x+ne2mε0x=0
This gives ωp=√ne2mε0=1.645×1016s−1
as the plasma frequency for the problem,.View SolutionQuestion 95
An oscillating circuit consisting of a capacitor with capacitance C and a coil of inductance L maintans free undamped oscillations with voltage amplitude across the capacitor equal to Vm. For an arbitrary moment of time find the relation between the current I in the circuit and the voltage V acroos the capacitor. Solve this problem usdini Ω's law and then the energy conservation law. View SolutionQuestion 96
An oscillating circuit consists of a capacitor with capacitance C, a coil of inductance L with negligible resistance, and aswitch. With the switch disconnected , the capacitor was charged to a voltage Vm and then at the moment t=0 the switch was closed . Find :
(a) the current (I(t)) in the circuit as a function of time,
(b) the emf of self- inductance in the coil at the moments when the electric energy of the capacitor is equal to that of the current in the coil. View SolutionQuestion 97
In an oscillating circuit consisting of a parallel- plate capacitor and an inductance coil with negligible active resistance the oscillations with energy W are sustained. The capacitor plates were slowly drawn aparto to increase the oscillation frequency η− fold. What work was doen in the process ?View SolutionQuestion 98
In an oscillating circuit shown in figure, the coil inductance is equal to L=2.5μF. The capacitor have capacitances C1=2.0μF and C2=3.0μF. The capacitors were charged to a voltage V=180V, and then the switch Swwas closed. Find :
(a) the natural oscillation frequency,
(b) the peak value of the current flowing through the coil.
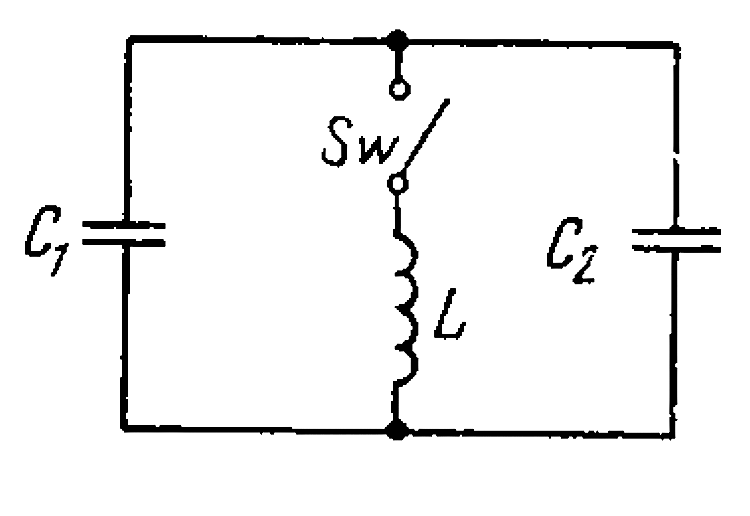 View Solution
View SolutionQuestion 100
An oscillating circuit consists of an inductance coil L and a capacitor with capacitance C. The resistance of the coil and the lead wires is negligible . The coil is placed in a permanent magnetic filed so that the total flux passing through all the turns of the coild is equal to Φ . At the moment t=0 the magnetic field was switched off. Assuiming the switching off time to be negligible compared to the natural oscillation paeriod of the cirucuit, find the circuit current as a fuction of time tView SolutionQuestion 102
A certain oscillating circuit consits of a capacitor with capacitance C, a coil with inductance L and active resistance R, and a switch . When the swith was disconnected, the capacitor was charged, then the switch was closed and oscillations set in. Find the ratio of the voltage across the capacitor to its peak value at the moment immediatel after closing the switch. View SolutionQuestion 104
An oscillating circuit consist of a capacitor with capacitance C=4.0μF and a coil with inductance L=2.0μH and active resistance R=10Ω. Find the ration of the energy of the coil's magnetic field to that of the capacitor's electric field at the moment when the current has the maximum value . View SolutionQuestion 105
An oscillating circuit consists of two coils connected in series whose inductances are L1 and L2 active resistances are R1 and R2 , and mutual inductance is negligible. These coils are to be replaced by one, keeping the frequency and the quality factor of the circuit constant. Find the inductance and the active resistance of such a coil. View SolutionQuestion 109
In a circuit shown in figure the battery emf is equal to E=2.0V, its internal resistance is r=9.0Ω, the capacitance of the capacitor is C=10μF, the coil inductance is L=100mH, and the resistance is R=100Ω . At a certain momenta the switch Sw was disconneted.
Find the energy of oscillations in the circuit
(b) t=0.30s after the switch was disconnected,
 View Solution
View SolutionQuestion 111
An oscillating circuuit incorporates a leaking capacitor. Its capacitance is equal C and active resistance to R. The coil inductance is is L. The resistance of the coil and the wires is negligible. Find :
(a) the damped oscillation frequecy of such a circuit ,
(b) its quality factor. View SolutionQuestion 112
Find the quality factor of a circuit with capacitance C=2.0μF and inductance L=5.0mH if the maintenance of undamped oscillations in the circuit with the voltage amplitude across the capacitor being equal to Vm=1.0V requires a power (:P:)=0.10mW. The damping of oscillations is sufficiently lowView SolutionQuestion 114
An oscillating circuit consists of a capacitor with capacitance C=1.2nF and a coil with inductance L=6.0μH and active resistance R=0.50Ω. What mean power should be fed to the circuit to maintain undamped harmonic oscillations with volage amplitude acroos the capacitor being equal to Vm=10V?View SolutionQuestion 116
There are two oscillating circuits (figure) with capacitors of equal capacitances. How must inductances and active resistances of the coils be interrelated for the frequencies and damping of free oscillations in both circuits to be equal ? The mutual inductance of coils in the left circuit is negligible.
 View Solution
View SolutionQuestion 117
A circuit consists of a capacitor with capacitance C and a coil of inductance L connected in series, as well as a switch and a resistance equal to the critical value for this circuit. With the switch disconnected, the capacitor was charged to a voltage V0, and at the moment t=0, the switch was closed . Find the corrent I in the circuit as a function of time t.What is Imax equal to ?View SolutionQuestion 120
A long one− layer solenoid tightly would of wire with resistivity ρ has n turns per unit length. The thickness of the wire insulation is negligible. The cross− sectional radius of the solenoid is equal to a. Find the phase difference between current and alternating voltage fed to the solenoid with frequency v. View SolutionQuestion 121
A circuit consisting of a capacitor and an active resistance R=110Ω connected in series is fed an alternating voltage with amplitude Vm=110V. In this case the amplitude of steady − state current is equal to Im=0.50A. Find the phase difference between the current and the voltage fed. View SolutionQuestion 124
A series circuit consisting of a capacitor with capacitance C=22μF and a coil with active resistance R=20Ω and iniductance L=0.35H is connected to a source of alternating voltage with amplitude Vm=180V and frequency ω=314s−1. Find :
(a) the current amplitude in the circuit,
(b) the phase difference between the current and the external voltage ,
(c) the amplitudes of voltage across the capacitor and the coil. View SolutionQuestion 125
A series circuit consisting of a capacitor with capacitance with capacitance C, a rasistance R, and a coil with inductance L and negligible active resistance is connected to an oscillator whose frequency can be varied without changing the voltag amplitude. Find the frequency at which the voltage amplitude is maximum
(a) across the capacitor ,
(b) across the coil. View SolutionQuestion 126
An alternating voltage with frequency ω=314s−1 and amplitude Vm=180V is fed to a series circuit consisting of a capacitor and a coil with active resistor's capacitance will the voltage amplitude across the coil be maximum ? What is this amplitude equal to ? What is the corresponding voltage amplitude across the condenser ?View SolutionQuestion 127
A capacitor with capacitance C whose interelectrode space is filled up with poorly conducting medium with active resistance R is connected to a source of alternating voltage V=Vmcosωt. Find the time dependence of the steady − state current flowing in lead wires. The resistance of the wires is to be neglected. View SolutionQuestion 128
An oscillating circuit consists of a capacitor of capacitance C and a solenoid with inductance L1. The solenoid is inductively connected with a short− circuited coil having an inductance L2 and a negligible active resistance. Their mutual inductance coefficient is eqaul to L12. Find the natural frequency of the given oscillating ciruit. View SolutionQuestion 130
An oscillating circuit consisting of a coil and a capacitor connected in series if fed an alternating emf, with coil inductance being chosen to provide the maximum current in the circuuit. Find the quality factor os the system, provided an n−fold increase of inductance results in an n− fold decrease of current in the circuit. View SolutionQuestion 131
A series circuit consisting of a capacitor and a coil with active resistance is connected to a source of harmonic voltage whose frequency can be aried, keeping the voltage amplitdue are n times less than the resonance amplitude. Find :
(a) the resonance frequency,
(b) the quality factor of the circuit. View SolutionQuestion 132
Demonstrate thatat low damping the quality factor Q of a circuit maintaining forced oscillations is approximately equal to ω0/Δω, where ω0 is the natural oscillation frequency , Δω is the width of the resonance curve I(ω) at the " height " which is √2 times less than the resonance current amplitude. View SolutionQuestion 133
A circuit consisting of a capacitor and a coil connected in seried if fed two alternating voltages of equal amplitudes but different frequencies. The frequency of one voltage is equal to the natural oscillation frequency (ω0) of the circuit, the frequency of the other voltage is η times highter. Find the ratio of the current amplitudes (I0/I) generated by the two voltages if the quality factor of the system is equal to Q. Calculate this ratio for Q=10 and 100, if η=1.10. View SolutionQuestion 136
A solenoid with inductance L=7mH and active resistance R=44Ω is first connected to a source of direct voltabe V0 and then to a source of sinusoidal voltage with effective value V=V0 . At what frequency of the oscillator will be power consumed by the solenoid be η=5.0 times less than in the former case ?View SolutionQuestion 138
A coil with inductance L=0.70H and active resistance r=20Ω is connected in series with an inductance − free resistance R. An alternating voltage with effective value V=220V and frequency ω=314s−1 is a applied across the terminals of this circuit. At what value of the resistance R will the maximum heat power be generated in the circuit ? What is it equal to ?View SolutionQuestion 140
A source of sinusoidal emf with constant voltage is connected in series with an oscillating circuit with quality factor Q=100. At a certain frequency of the external voltage the heat power generated in the circuit reached the maximum value. How much ( in per cent) should this frequency be shifted to decrease the power generated n=2.0 times ?View SolutionQuestion 141
A series circuit consisting of an inductance − free resistance R=0.16kΩ and coil with active resistance is connected to the mains with effective voltabe V=220V. Find the heat power generated in the coil if the effective voltage values across the resistance R and the coil are equal to V1=80V and V2=180V respectively. View SolutionQuestion 144
Draw the approcimate vector diagrams of currents in the circuits shown in figure. The voltage applied across the points A and B is assmed to be sinosoidal, the parameters of each circuit are so chosen that the total current I0 lags in phase behind the external voltage by an angle φ.
 View Solution
View SolutionQuestion 145
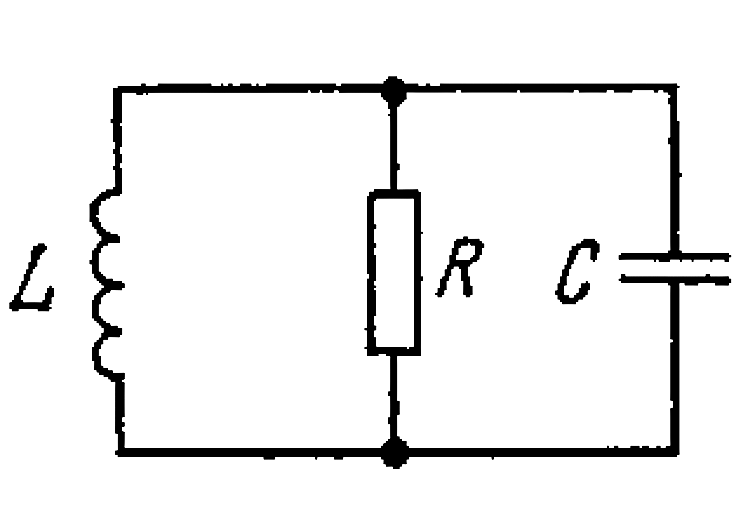
A capacitor with capacitance C=1.0μF and a coil with active resitance R=0.10Ω and inductance L=1.0mH are connected in parallel to a source of sinusoidal voltage V=31V. Find :
(a) the frequency ω at which the resonance sets in ,
(b) the effective value of the fed current in resonance , as well as the corresponding currents flowing through the coil and through the capacitor. View SolutionQuestion 148
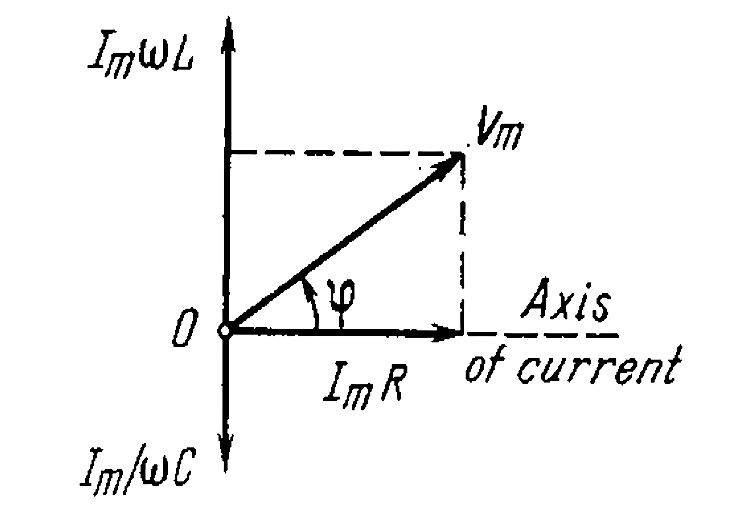
A ring of thin wire with active resistance R and inductance L rotates with constant angular velocity ω in the external uniform magneitce field perpendicular to the rotation axis. In the process , the flux of magnetic induction of external field across the ring varies with time as Φ=Φ0cosωt. Demonstrate that
(a) the inductive current in the ring varies with time as I=Imsin(ωt−φ), where Im=.mΦ/√R2+ω2L2 with tanφ=ωL/R,
(b) the mean mechanical is defined by the formula P=1/2ω2Φ20R/(R2+ω2L2). View SolutionQuestion 149
A wooden core ( figure ) supports two coils : coil 1 with inductance L1 and shor − circuited coil 2 with active resistance R and inductance L2. The mutual inductance of the coils depends on the distance x between them according to the law L12(x). Find the mean ( averaged over time ) value of the interaction force between the coils when coil 1 carries an alternating current I1=I0cosωt
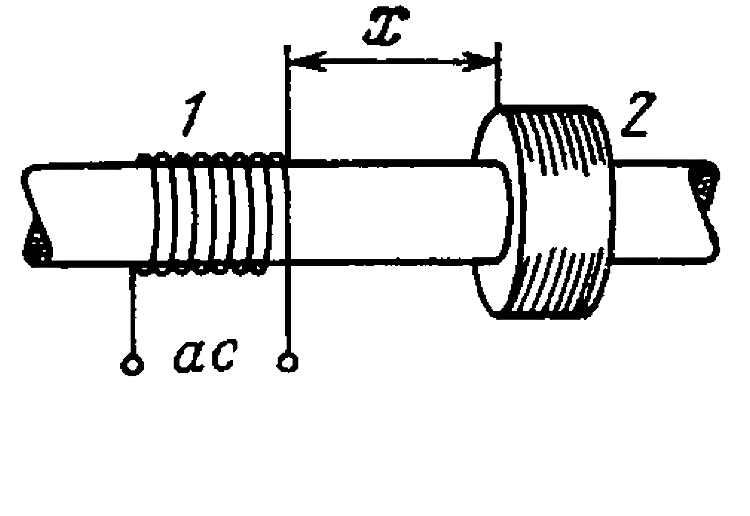 View Solution
View SolutionQuestion 155
The equation of a travelling plane sound wave has the form y=60cos(1800t−5.3x), where y is in micrometres, t in seconds and x in metres. Find
(a). The ratio of the displacement amplitude with which the particle of the medium oscillate to the wavelength,
(b).the velocity oscillation ammplitude of particles of the medium and its ratio to the wave propagation velocity , (c). the particle acceleration amplitude. View SolutionQuestion 156
A plane wave ξ=acos(ωt−kx) propagates in a homongeneous elastic medium, For the moment t=0 draw
(a) the plots of ξ,δξ/δt, and δξ/δx vs x,
(b) velocity medium direction of the particle of the medium at the points where ξ=0, for the cases of longitudinal and transverse waves,
(c) the approximate plot of density distribution ρ(x) of the medium for the case of longitudinal waves. View SolutionQuestion 157
A plane elastic wave ξ=ae−γxcos(ωt−kx), wherea,γ,ω, and k are constants , propagates in a homogeneous medium. Find the phase difference between the oscillations at the points where the particles, displacement amplitudes differ by η=1.0%, if γ=0.42m−1 and the wavelength is λ=50cm. View SolutionQuestion 158
Find the radius vector defining the position of a point source of spherical waves if that source is known to be located on the straight line between the points with radius vector r1 and r2 at which the oscillation amplitudes of particls of the medium are equal to a1 and a2. The damping of the wave is negligible, the medium is homogeneous. View SolutionQuestion 159
A point isotropic source generates sound oscillations with frequency v=1.45kHz. At a distance r0=5.0m from the source the displacement amplitude of particles of the medium is equal to the a0=50μm, and at the point A located at a distance r=10.0m from the source the displacement ampitude is η=3.0 times less than a0 . Find :
(a) the damping coefficient γ of the wave,
(b0 the velocity oscillation amplitude of particles of the medium at the point A. View SolutionQuestion 160
Two plane waves propagate in a homogeneous elastic medium, one along the x axis and the other along the y axis :ξ1=acos(ωt−kx),ξ2=acos(ωt−ky) . Find the motion pattern fo particles in the plane xy if both waves.
(a) are tansverse and their oscillation directions coincide,
(b) are longitudinal. View SolutionQuestion 161
A plane undamped harmonic wave propagates in a medium. Find the mean space density of the total oscillation energy (:w:), if at any point of the medium the space density of the total oscillation energy becomes equal to w0 one− sixth of an oscillation perio after passing the displacement maximum View SolutionQuestion 162
A point isotropic sound source is located on the perpendicular to the plane of a ring drawn through the centre O of the ring. The distance between the point O and the source is l=1.00m, the radius of the ring is R=5.00m. Find the mean energy flow across the area enclosed by the ring if at the point O the intensity of sound is equal to I0=30μW/m2. The damping of the waves is negligible. View SolutionQuestion 163
A point isotropic source with sonic power P=0.10W is located at the centre of round hollow cylinder with radius R=1.0m and height h=2.0m. Assuming the sound to be completely absorbed by the walls of the cylinder, find the mean energy flow reachind the lateral surface of the cylinder. View SolutionQuestion 164
The equation of a plane standing wave in a homogeneous elastic medium has the form ξ=acoskx.Cosωt. Plot :
(a) ξ and δξ/δx as functions of x at the moments t=0 and t=T/2, where T is the oscillation period,
(b) the distribution of density ρ(x) of the medium at the moments t=0 and t=T/2 in the case of longitudinal oscillation ,
(c) the velocity distribution of particles of the medium at the moment t=T/4 , indicate the directions of velocities at the antinodes, both for longitudinal and transverse oscillation. View SolutionQuestion 165
A longitudinal standing wave ξacoskx.Cosωt is maintained in a homogeneous medium of density ρ. Find the expressions for the space density of
(a) potential energy wp(x,t),
(b) kinetic energy wk(x,t),
Plot the space density distribution of the total energy w in the space between the displacement nodes at the moments t=0 and t=T/4, where T is oscillation period. View SolutionQuestion 169
To determine the sound propagation velocity in air by acoustic resonance technical one can use a pipe with a piston and a sonic membrane closing one of its ends. Find the velocity of sound if the distance between the adjacent positions of the piston at which resonance is observed at a frequency v=2000Hz is equal to l=8.5cm.View SolutionQuestion 172
A string of mass m is fixed at both ends. The fundamental tone oscillations are excited with circular frequency ω and maximum displacement amplitude amax . Find :
(a) the maximum kinetic energy of the string,
(b) the mean kinetic energy of the string averaged over one oscillation period. View SolutionQuestion 174
A source of sonic oscillations with frequency v0=100Hz moves at right angles to the wall with a velocity u=0.17m/s. Two stationary receivers R1 and R2 are located on a straight line, coinciding with the trajectory of the source , in the following succession :R1− source −R2− wall. Which receiver registers the beatings and what is the beat frequency ? The velocity of sound is equal to υ=340m/s. View SolutionQuestion 175
A stationary observer receives sonic oscillations from two tuning forks one of which approaches and the other recedes with the same velocity. As this takes place, the observer hears the beats of frequency f=2.0HZ. Find the velocity of each tuning fork if their oscillation frequency is fo=680HZ and the velocity of sound in air is υ=340m/s. View SolutionQuestion 176
A receiver and a source of sonic oscillations of frequency v0=2000Hz are located on the x axid. The source swings harmonically along that axis with a circulat frequency bandwidth registered by the stationary receiver be equal to Δv=200Hz ? The velocity of sound is equal to v=340m/s. View SolutionQuestion 177
A source of sonic oscillations with frequency v0=1700Hz and a receiver are located at the same point. At the moment t=0 the source starts receding from the receiver with constant acceleration w=10.0m/s2. Assuing the velocity of sound to be equal to v=340m/s, find the oscillation frequency registered by the stationary receiver t=10.0safter the start of motion. View SolutionQuestion 178
A source of sound with natural frequency f0=1800Hz moves uniformly along a straight line separated from a stationary observer by a distance l=250m. The velocity of the source is equal to η=0.80 fraction of the velocity of the sound.
Q. Find the frequency of osund received by the observer at the moment when the source gets closest to him.
 View Solution
View SolutionQuestion 180
A source of sonic oscillations with frequency n=1700Hz and a receiver are located on the same normal to a wall. Both the source and receiver are stationary, and the wall recedes from the source with velocity u=6.0ms. Find the beat frequency registered by the receiver. The velocity of sound is v=340ms.View SolutionQuestion 182
A plane sound wave propagates along the x axis . The damping coefficient of the wave is γ=0.0230m−1. At the point x=0 the loudness level is L=60dB. Find :
(a) the loudness level at a point with coordinate x=50m,
(b) the coordinate x of the point at which the sound is not heard any more. View SolutionQuestion 184
An observer A located at a distance rA=5.0m from a ringing tuning fork notes the sound to fade away τ=19s later than an observer B who is located at a distance rB=50m from the tuning fork. Find the damping coefficient β of oscillations of the tuning fork. The sound velocity v=340m/s. View SolutionQuestion 185
A plane longitudinal harmonic wave propagates in a medium with density ρ. The velocity of the wave propagation si v . Assuming that the density variations of the medium, induced by the propagating wave, Δρ<<ρ , demonstrate that ltbr> (a) the pressure increment in the medium Δp=−ρv2(δξ/δx), whereδξ/δx is the relative deformation,
(b) the wave intensity is defined by Eq. (4.3i)View SolutionQuestion 186
A ball of radius R=50cm is located in the way of propagation of a plane sound wave. The sonic wavelength is λ=20cm, the frequency is v=1700Hz, the pressure oscillation amplitude in air is (Δp)m=3.5Pa. Find the mean energy flow, averaged over an oscillation period, reaching the surface of the ball. View SolutionQuestion 187
A point A is located at a distance r=1.5m from a point source of sound of frequency 600HZ. The power of the source is 0.8W. Speed of sound in air is 340m/s and density of air is 1.29kg/m3. Find at the point A, (a) the pressure oscillation amplitude(Δp)m (b) the displacement oscillation amplitude A.View SolutionQuestion 188
At a distance r=100m from a point isotropic source of the sound of frequency 200Hz the loudness level is equal to L=50dB. The audiblitiy threshold at this frequency corresponds to the sound intensity I0=0.10nW/m2. The damping coefficient of the sound wave is γ=5.0.1.0−4m−1 . Find the sonic power of the source. View SolutionQuestion 190
A plane electromagnetic wave falls at right angles to the surface of a plane − parallel plate of thickness l . The plate is made of non− magentic substance whose permittivity decreases exponentially from a value ε10 at the front surface down to a value ε2 at the rear one. How lond does it take a given wave phase to travel across this plate gt View SolutionQuestion 197
A plane harmonic electromagnetic wave with plane polarization propagates in vacuum. The elctric component of the wave has a strength amplitude Em=50mV/m, the frequency is v=100MHz. Find :
(a) the efficient value of the displacement current density ,
(b) the mean energy flow density averaged ove an oscillation period. View SolutionQuestion 198
A ball of radius R=50cm is located in a non− magnetic medium with permittivity ε=4.0. In that medium a plane electromagnetic wave propagates, the strength amplitude of whose electri component is equal to Em=200V/m. What amount of energy reaches the ball during a time interval t=1.0min ? View SolutionQuestion 199
A standing electromagnetic wave with electric component E=Emcoskx.Cosωt is sustained along the x axis in vacuum. Find the magnetic component of the wave B(x,t). Draw the approximate distribution pattern of the wave's electric and magnetic components (E and B) at the moments t=0 and t=T/4, where T is the oscillation period. View SolutionQuestion 203
A parellel-plate capacity whose electrodes are shaped as round disc is changed slowly. Demonstrate that the flux of the Poynting vector across the capacitor's lateral surface is equal to the increment of the capcitor's enegry per unit time. The dissipation of field at the edge is to be neglected in calculations.View SolutionQuestion 206
A current flowing in the winding of a long straight solenoid is increased at a sufficiently slow rate. Demonstrate that the rate at which the enrgy of the magnetic field in the solenoid increases is equal to the flux of the Poynting vector across the lateral surface of the solenoid.View SolutionQuestion 207
Fig. illustrates a segment of a double line carrying direct current whose direction in indicated by the arrows. Taking into account that the potential φ2>φ1, and making use of the Poynting vector, establish on which side (left or right) the source of the current is located.
 View Solution
View SolutionQuestion 208
The enegry is transferred form a source of constant voltage V to a consumer by means of long straight coaxial cable with negligible active resistance. The consumed current is I. Final the enegry flux across the cross-section of the cable. The conductive sheath is supposed to be thin.View SolutionQuestion 209
A source of ac volatge V=V0cosωt delivers enegry yo a consummer by means of along straight coaxial cable with negligible active resistance. The current in the circuit varies as I=I0cosωt−φ. Find the time-averaged enegry flux through the cross-section of the cable. The sheath is thin.View SolutionQuestion 214
A particle with charge e and mass m flies with non-relativistic velocity v at a distance b past a stationary particle with charge q. Neglecting the bending of the trajectory of the moving particle, find the enegry lost by this particle due to radiation during the total flight time.View SolutionQuestion 216
A non-relativistic enegry particle moves in a transverse uniform magnetic fiel with induction B. Find the time dependence of the particles's kinetic enegry diminshing due to radiation. How soon will its kinetic enegry decrease e-fold? Calculate this time interval for the case (a) of an electron, (b) of a proton.View SolutionQuestion 217
A charged particle moves along the y axis according to the law y=acosωt, and the point of observation P is located on the x axis at a distance l from the particle (l>>a). Find the ratio of electromagnetic radiation flow densities S1/S2 at the point P at the moments when the corrdinate of the particle y1=0 and y2=a. Calculate that ratio if ω=3.3.106s−1 and l=190m. View SolutionQuestion 218
A charged particle moves uniformaly with velocity v along a circle of radius R in the plane xy (fig.) An observer is located on the x axis at a point P which is removed form the centre of the circle by a distance much exceeding R. Find:
(a) the relatiship between the observed values of the y projection of the particle's acceleration and the y corrdinate of the particle:
(b) the ratio of electromagnetic radiation flow densities S1/S2 at the point P at the moments of time when the particle moves, form the standpoint of the observer P, toward him and away from him, as shwon in the figure.
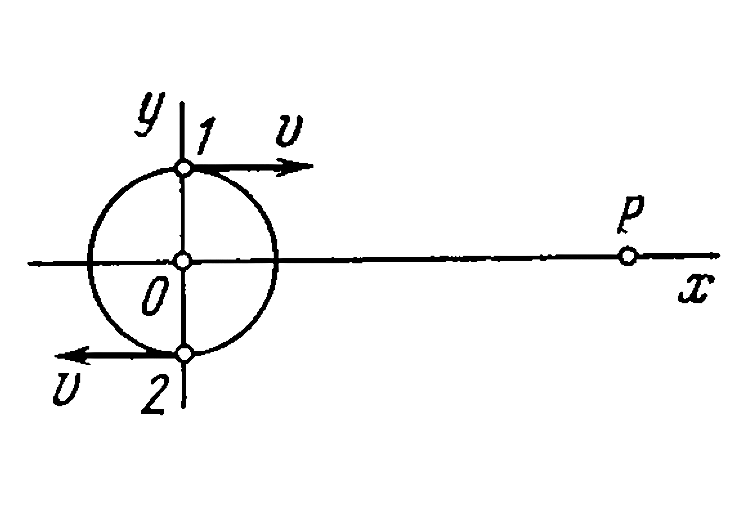 View Solution
View SolutionQuestion 219
An electromagnetic wave emitted by an elementary dipole propagates in vacuum so that in the far fold zone the mean value of the enrgy flow density is equal to S0 at the point removes from the dipole by a distance r along the perpendicualr draws to the dipole's axis. Find the mean radiation power of the dipole.View SolutionQuestion 222
A free electron is located in the field of a plane electromagnetic wave. Neglecting the magnetic component of the wave distrurbing its motion, find the ratio of the mean energy radiated by the oscillating electron per unit time to the mean value of the energy flow density of the incident wave.View SolutionQuestion 223
A plane electromagnetic wave with frequency ω falls upon an elastically bonded electron whose natural frequency equals ω0. Neglecting the damping of oscillations, find the ratio of the mean enegry dissipated by the electron per unit time to the mean value of the enrgy flow density of the incident wave. View SolutionQuestion 224
Assuming a particle to have the form of a ball and to absorb all incient light, find the radius of a particle for which its gravitational attraction to the sun is counterbalanced by the forces that light exerts on it. The power of light raiated by the sun equals P=4.1026W, and the density of the particle is ρ=1.0g/cm3.View Solution